Petri Net Overview
Petri nets are a descriptive model of discrete event systems proposed by Petri in 1962, which will represent the relationship between asynchronous and parallel events and the states that guide them in an event-driven system. Petri Net is a graphical model of states and transitions, and it is a very flexible and general modeling language consisting of four structural elements, namely the combination of place P, transition T, input relation I, and output relation O (PTIO), and marking M.
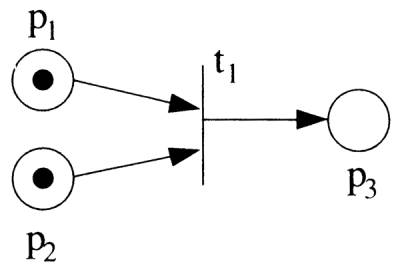
An example of Petri net operation is represented in the figure below. When there are inputs from places p1 and p2 to transition t1 and outputs are given to p3, if there are tokens (black circles) representing markings (black circles) at p1 and p2, t1 fires and moves to p3 as a single token.

Petri nets are used in numerous fields, and in particular, they are widely used models in parallel processing, distributed processing, automata theory, software engineering, and business process modeling.
There are several types of Petri nets, the most common of which are called “simple Petri nets. Simple Petri nets have the following elements.
- Places: Circular nodes representing states
- Transitions: square nodes representing changes in state
- Retractor lines (input lines): lines that represent locations needed for transitions to fire
- Output lines: lines that represent places used to transition to the next state as a result of a transition firing
Simple Petri nets are particularly useful for modeling parallel processing; for example, a simple Petri net can model a situation where multiple processes are running concurrently, each running independently and not needing to wait for another process to finish.
Petri nets are also a useful tool for business process modeling. Each step in a process can be represented as a node, and the dependencies between steps can be represented as edges. This also allows us to identify areas for improvement to increase the efficiency of the process.
Simple Petri nets have limitations and can generally only model relatively simple problems. For this reason, various types of extended Petri nets have been developed. Some extended Petri nets are described below.
- Colored Petri Nets: Colored Petri Nets allow the addition of a “color” attribute to each token. This allows one to specify how a token behaves depending on its state or transition state. For example, if a token in state A is color 1 and a token in state B is color 2, they are treated separately.
- Timed Petri Nets: Timed Petri Nets allow transitions to be assigned the time needed to execute. It can also record the time that a token enters a state and the time that a transition is executed. This allows modeling of time-related issues.
- Hierarchical Petri Nets: Hierarchical Petri Nets allow multiple simple Petri Nets to be combined in a hierarchical manner. This allows complex problems to be partitioned and handled.
- Real-Time Petri Nets: In Real-Time Petri Nets, the speed at which tokens move can be specified. It is also possible to include factors such as the current time and the position of the token in the conditions under which the transition is performed.
- Stochastic Petri Nets: Stochastic Petri Nets allow the user to specify the probability of each transition occurring. The time required to perform the transition can also be treated as a stochastic variable. This makes them applicable when the behavior of the system includes stochastic elements.
Petri-net Application Examples
Petri nets are widely used for system modeling and analysis. Some specific applications are shown below.
- Modeling of manufacturing processes: Petri nets are well suited for modeling manufacturing processes. Using Petri nets, the various elements of a manufacturing line, such as machines, workers, conveyors, quality inspections, etc., can be represented as nodes and their behavior can be simulated using tokens. This allows us to identify improvements to optimize the efficiency of the manufacturing process.
- Software design: Petri nets are also suitable for software design. Perinets can be used to help represent the control flow of a program. For example, it can be used to model the control flow as users perform various actions within an application.
- Network Analysis: Petri nets are also used for network traffic analysis and protocol design. When using Petri nets for network analysis, for example, nodes are used as communication protocols and tokens are used to represent data packets. These can be used to visualize communication flows and identify network bottlenecks.
- Business Process Modeling: Petri Nets are also used for modeling business processes. Using Petri nets, nodes represent steps in a business process and tokens represent the state of the business process. These can be used to study the automation and optimization of business processes.
- Healthcare: PetriNets can be applied to modeling patient conditions and treatment processes in the healthcare sector. For example, it can be used to model the process from patient admission to discharge and the execution of treatment plans to help improve the efficiency and quality of medical care.
- Rail systems: Petri-net can be used to model rail transportation in rail systems. For example, modeling of train arrival and departure times, route selection, and signal control can be used to improve the efficiency and safety of rail transportation.
Petri Net and Artificial Intelligence Technology
Petri nets are suitable for the application of artificial intelligence technology due to the flexibility of their structure. Some examples of the application of artificial intelligence technologies to Petri nets are described below.
- Self-diagnosis of control systems based on Petri nets: Petri nets are sometimes used for modeling complex control systems. Artificial intelligence techniques can be used to enable self-diagnosis of such systems. For example, the various anomaly detection algorithms described in “Anomaly Detection and Change Detection Techniques” can be used to automatically detect anomalies in a system.This can be done in the following steps
-
- Petri net construction: First, a Petri net of a normal process is constructed. This Petri net represents the transitions that should be taken in the case of normal operation.
- Data collection and preprocessing: Next, the data collected from the process is preprocessed. This process includes data cleaning, scaling, and feature selection.
- Training of anomaly detection models: After learning the normal behavior of the process using Petri nets, a machine learning model is trained. This model is used to detect anomalous behavior by comparing it to the normal behavior defined by the Petri net.
- Identifying the cause of the anomaly: If the machine learning model detects an anomaly, the Petri net can be used to identify its cause. If a particular part of the Petri net is causing the anomaly, it is more likely to be the cause of the anomaly.
- Solving the Problem: Once the cause of the anomaly has been identified, action can be taken to correct the problem. Using Petri nets, after correcting the problem, the model can be trained again to improve its accuracy in detecting anomalies.
- Petri Net-based business process optimization: Business processes can be modeled using Petri Nets. By using artificial intelligence techniques such as those described in “Workflow & Service Technology” process bottlenecks can be identified and remedies can be proposed.Below we describe a typical algorithm for identifying bottlenecks in business processes using Petri nets.
-
- Heuristics Miner: Heuristics Miner is an algorithm proposed by P.A. Van der Aalst et al. that can identify bottlenecks in business processes using unsupervised learning. The algorithm identifies process bottlenecks by analyzing Petri nets, which are automatically generated from actual transactions.
- Alpha Miner: Alpha Miner is an algorithm that constructs Petri nets from transaction data of business processes using unsupervised learning. The algorithm automatically generates Petri nets from transaction data and analyzes the network to identify process bottlenecks.
- Conformance Checking: Conformance Checking is an algorithm used to detect differences between the actual process and the designed process, and is capable of learning Petri net models using supervised learning. The algorithm identifies process bottlenecks by comparing actual transaction data with the Petri net model and analyzing the differences.
- Robot control based on Petri nets: An approach to modeling using Petri nets is also being considered. This allows the robot to autonomously adapt to its environment using reinforcement learning algorithms, such as those described in “Theory and Algorithms of Various Reinforcement Learning Techniques and their Implementation in Python” for example, using model-based Q-learning algorithms, in the following steps This is done by.
-
- Creating a Petri net: First, a Petri net is created that corresponds to the task that the robot should control. A Petri net consists of a network of states and transitions, and each state is assigned an action.
- Define the environment: Next, define the environment in which the robot will operate. For example, if the robot is to grasp an object, it defines the position and posture of the object to be grasped, the position of surrounding obstacles, etc.
- State awareness: The robot uses cameras, sensors, etc. to understand its current state. For example, when performing an object grasping task, the robot knows the position and posture of the object to be grasped.
- Action selection: The robot selects the action to be performed based on the current state. For example, when performing the task of grasping an object, the robot selects the position and posture of the grasping arm.
- Calculation of reward: The robot calculates the reward according to the action it has selected. For example, when performing the task of grasping an object, a higher reward is given if the robot is able to grasp the object accurately.
- Parameter update: The robot updates its own parameters based on the reward. The parameters are weights, biases, and other values that control the robot’s behavior.
- Iteration: Repeat the above steps and the robot learns more efficient actions. Finally, the robot can choose the best action based on the Petri net.
- Software testing based on Petri nets: Software testing can be modeled using Petri nets. Artificial intelligence techniques can be used to automate testing. For example, a software system can be modeled using Petri nets by understanding and modeling the software functionality and control flow, defining appropriate initial conditions, and then using heuristics algorithms such as those described in “Overview and References on Meta-heuristics” or probabilistic generative models such as those described in “About Probabilistic Generative Models” can be used to automatically generate test data to enable self-diagnosis, optimization, and autonomous control of the system.
-
- Random Walk Algorithm: The random walk algorithm described in “Overview of Random Walks, Algorithms, and Examples of Implementations” would be an algorithm that randomly selects an event on a Petri net and moves to the transition connected to that event. Although this algorithm can search all states on the Petri net equally, it is not suitable for efficient test case generation.
- Monte Carlo tree search algorithm: The Monte Carlo tree search algorithm described in “Overview of Monte Carlo Tree Search and Examples of Algorithms and Implementations” randomly generates a test case for each selected event on the Petri net and evaluates the probability of success for that test case. This is repeated to search for the most effective test case.
- Genetic Algorithm: The genetic algorithm described in “Overview of genetic algorithms, application examples, and implementation examples” will be an algorithm that uses genetic manipulation to generate combinations of test cases. It randomly generates an initial set of test cases, selects the most effective test case from that set, and generates the next set. This is repeated to search for the most effective set of test cases.
- Statistical Model Checking Algorithm: The Statistical Model Checking Algorithm will be an algorithm that statistically models combinations of events occurring on Petri Nets and generates effective test cases. This algorithm calculates the frequency and probability of events occurring on Petri nets and generates the most effective test cases based on this information.
Examples of concrete implementations of Petri nets
Petri Net systems are incorporated into programmable logic controller (PLC) control systems, into software systems that incorporate Petri Nets into Activity Diagrams, which are part of the Unified Modeling Language (UML) Some of them are embedded in design and analysis systems, and some of them are embedded in production control systems and robot control systems.
In this section, we describe examples of implementations in Python, Java, and Clojure.
Implementation in Python
Python has libraries for implementing petri nets, such as petri-net and Simpy.
Implementation in Java
To implement Petri nets in Java, libraries such as PNlib、PIPE2(Platform Independent Petri net Editor 2)、and PetriNetSim can be used.
Implementation by Clojure
As mentioned above, to implement complex Petri nets, it is necessary to implement native code. Here we show an example of implementing them by using core.async, a library of Clojure.
(require '[clojure.core.async :as async])
(defn make-place [name initial-tokens]
{:name name :tokens (async/chan (async/buffer initial-tokens))})
(defn make-transition [name input-places output-places]
(let [input-channels (map :tokens input-places)
output-channels (map :tokens output-places)]
(fn []
(async/go
(let [_ (async/<! (async/merge input-channels)) _ (async/>! (async/merge output-channels) :token)]
(recur))))))
(defn make-petri-net [places transitions]
(doseq [t transitions]
(doseq [p (concat (:inputs t) (:outputs t))]
(alter-meta! p assoc :petri-net true)))
{:places places :transitions transitions})
(defn fire-transition [t]
(t))
;; example
(let [p1 (make-place :p1 1)
p2 (make-place :p2 0)
t1 (make-transition :t1 [p1] [p2])]
(fire-transition t1))In the above code, the make-place function creates a place and the make-transition function creates a transition; the make-petri-net function creates a petri-net from a list of places and transitions, and the fire-transition function only fires the given transition, It will only fire the given transition.
“Visually designing distributed systems in Clojure” describes an evaluation of a distributed software system using Clojure to construct Petri nets. Tokengame, a Petri net library in Clojure, is used here, and WoPeD, a tool developed at the University of Karlsruhe to simulate Petri nets, is introduced and sample code is provided.

コメント