The difference between causation and correlation
Causality and correlation are important concepts in statistics and scientific research and are often confused. However, they are distinct concepts and differ in the following ways.
-
Causation: Causation refers to a direct relationship in which one event causes another. In other words, we say that there is a causal relationship when there is a cause and effect relationship where one event causes another event. A causal relationship is a cause and effect relationship in which one event causes the other event, and has a temporal order relationship in which the causal cause occurs first in time and the result occurs later.
-
Correlation: A correlation is a relationship in which two events change simultaneously with a certain trend or pattern. In other words, two events are said to be correlated if they tend to increase or decrease at the same time. A correlation indicates that there is a relationship between two events, but it does not indicate a direct causal relationship. Even when a correlation exists, it does not mean that there is a causal relationship; there may be a third factor involved between the two.
To give an example of the difference between causation and correlation, if birdsong can be heard at the time the sun rises, these events are temporally related but not directly causally related. The rising of the sun does not cause birdsong, nor does birdsong cause the rising of the sun. This would be an example of correlation but not causation.
Understanding the difference between causality and correlation is important in scientific research and data analysis, and to clearly elucidate causality, it is necessary to use various experimental design and causal inference methods, such as those described in “Statistical Causal Inference and Causal Search. In addition, to find correlations, regression analysis methods such as those described in “Regression Analysis Using Clojure (1) Single Regression Model” should be applied.
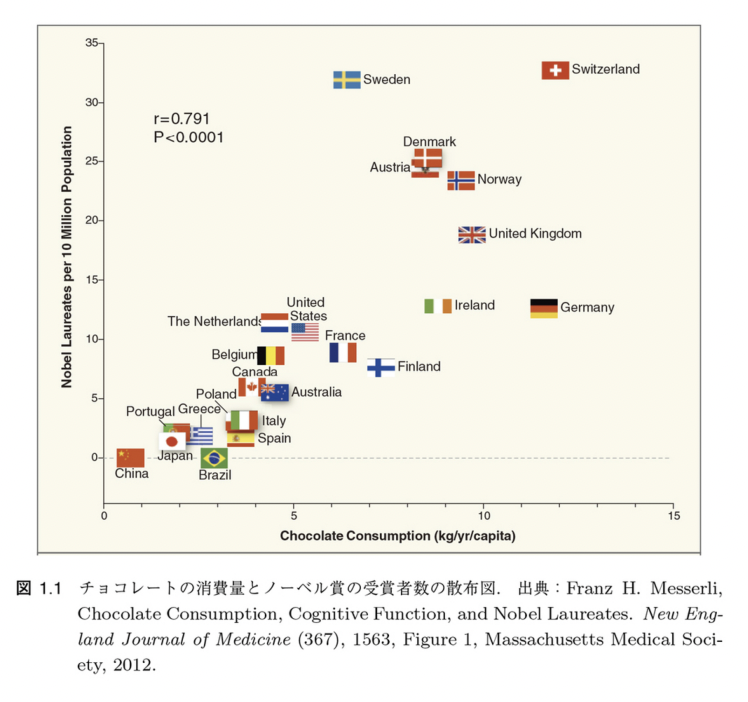
Here is another example that illustrates the difference between causality and correlation. The following is data on the consumption of chocolate and the number of Nobel Prize winners.

Looking at this data, there seems to be a clear correlation between the amount of chocolate consumed and the number of Nobel Prize winners, and one could conclude that eating chocolate is the only way to win a Nobel Prize.
In fact, Switzerland is home to many famous international research institutes that have produced many Nobel laureates, and this has almost nothing to do with the fact that it is the home of chocolate and has a high per capita consumption. If you perform machine learning and only look at the results without considering the original data, you may end up assuming that the results are “causal” or “correlative”.
To avoid such mistakes, in general natural science experiments, the preconditions (experimental conditions) are clearly defined and fixed, and then the causal relationship is determined by looking at the results when the conditions predicted as causes are changed. In the natural sciences, it is relatively easy to fix the preconditions in this way.
On the other hand, in humanities experiments (e.g., social sciences, such as the aforementioned chocolate and the Nobel Prize, or psychology, such as the reactions of people when given some kind of trigger), it is difficult to specify the factors that affect the results, so the method of randomly changing the possible conditions and then changing the causal The method of varying the parameters is often used. This is an image of breaking the chain of effects by randomizing the other conditions.
Mathematically, causality is based on a set model, based on the “binomial relationship” that we discussed earlier in the Foundations of Computer Mathematics.
As models to handle these causal relationships, we can use graphical models based on conditional probability as described in the Bayesian estimation previously mentioned, Bayesian models, or Markov logic networks as described in the previous section on SW and IOT, which express the relationship between cause and effect in terms of connections between nodes and edges.
As reference books on causal systems, there are “Causal Theory: Reading Causality from Real World Data – Iwanami Data Science 3“, “Statistical Causal Search“, “Philosophy of Causality“, and “The True Nature of Time: Deja Vu, Causality, and Quantum Theory“. The first two are based on graphical models, while the latter two are more philosophical discussions on the concepts of causality and time. The latter two are more philosophical and discuss concepts such as causality and time. Machine learning that takes the time axis into account is an advanced approach, and is still being presented at conferences.




The theme of causality is also taken up in philosophy and Zen. I would like to write about them another time. I would like to write more about statistical approaches such as this one in another occasion, where I will discuss actual use cases in more detail.

コメント