因果と相関の違いについて

因果と相関の違いについて

因果と相関は、統計学や科学的な研究において重要な概念であり、しばしば混同されることがある。しかし、それらは異なる概念であり、以下のように異なる。

• 因果関係（Causation）: 因果関係は、ある事象が別の事象を引き起こす直接的な関係を指す。つまり、ある事象が別の事象を引き起こす原因と結果の関係がある場合に因果関係があると言う。因果関係は、一方の事象が他方の事象を引き起こす原因と結果の関係であり、時間的にも因果的な因が先に起こり、結果が後に起こるという時間的な順序関係を持つ。

• 相関関係（Correlation）: 相関関係は、二つの事象が一定の傾向やパターンを持って同時に変化する関係を指す。つまり、二つの事象が同時に増加したり減少したりする傾向がある場合に相関関係があると言われる。相関関係は、二つの事象の間に関連性があることを示すが、直接的な因果関係を示すものではない。相関関係がある場合でも、因果関係があるわけではなく、両者の間には第三の要因が関係している可能性もある。

因果関係と相関関係のの違いを例で挙げると、太陽が昇る時間帯に鳥のさえずりが聞こえることがあるとしたとき、これらの事象は時間的に関連しているが、直接的な因果関係があるわけではない。太陽が昇ることが鳥のさえずりを引き起こすわけでもないし、鳥のさえずりが太陽の昇りを引き起こすわけでもない。これは相関関係があるが因果関係があるわけではない例となる。

因果関係と相関関係の違いを理解することは、科学的な研究やデータ分析において重要であり、因果関係を明確に解明するためには、”統計的因果推論と因果探索“に述べているような様々な実験設計や因果推論の手法を用いる必要がある。また、相関関係を求めるには”Clojureを用いた回帰分析(1) 単回帰モデル“等で述べているような回帰分析の手法を適用することとなる。

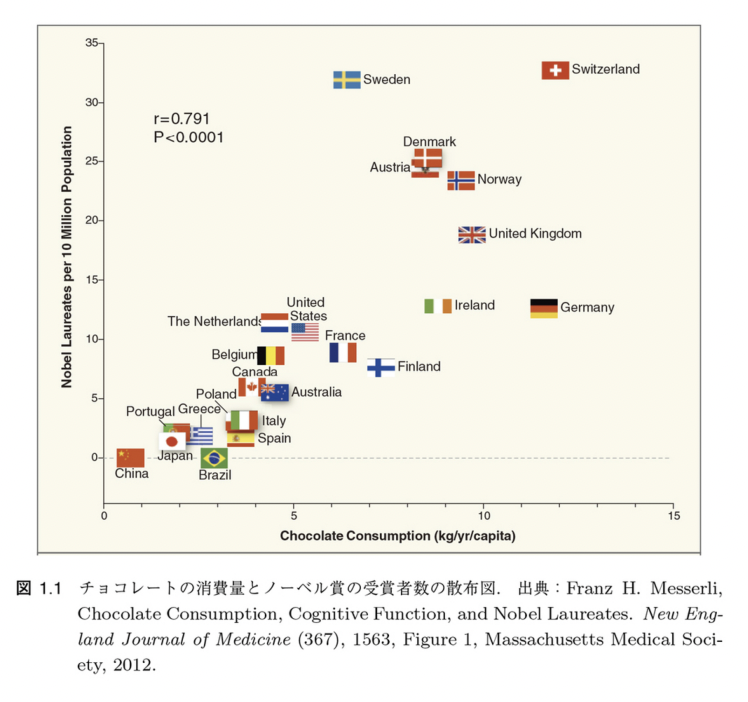
ここで因果関係と相関関係の違いを示すもう一つの例を示す。以下のようなチョコレートの消費量とノーベル賞の受賞者数のデータとなる。

このデータを見ると、チョコレートの消費量とノーベル賞の受賞者数には明らかに相関があるように見え、ノーベル賞を取るにはチョコーレートを食べれば良いという結論も導けてしまう。

実際には、スイスには有名な国際研究機関が多々ありそこから多数のノーベル賞受賞者が出ているのであり、チョコレートの本場で一人当たりの消費量が多いという事実とはほぼ関係がない。元のデータについての考察がないままに機械学習を行い結果だけを見てしまうと、このようにたまたまそうなっている結果を「因果関係」や「相関関係」としてしまうことがある。

そのような間違いを犯さないため、一般的な自然科学系の実験では前提条件(実験条件)を明確に定義して固定した上で、原因として予測する条件を変化させた時の結果を見て因果関係を判定する。自然科学の世界ではこのように比較的容易に前提条件を固定することが比較的容易だ。

それに対して、人文系の実験(例えば前述のチョコレートとノーベル賞のような社会科学系やなんらかのトリガーを与えた時人のリアクションのような心理学のケース)では、結果に影響を与える要因を規定することが困難なため、考えられうる条件をランダムに変化させた上で、原因のパラメータを変化させる手法がよく使われる。他の条件をランダムにすることで効果の連鎖を断ち切るイメージだ。

因果関係とは数学的には、以前コンピューターの数学の基礎で述べた「二項関係」を元に集合モデルをベースに考えることになる。

さらに、これら因果関係を扱うモデルとしては前述のベイズ推定で述べた条件付き確率を元にしたグラフィカルモデルやベイジアンモデルあるいは前回のSWとIOTで述べたマルコフロジックネットワークと呼ばれる原因と結果の関係をノードとエッジの繋がりで表すモデルを使うことができる。

因果系の参考図書としては「因果論実世界のデータから因果を読む-岩波データサイエンス3」、「統計的因果探索」、「哲学がわかる因果性」、「時間の正体 デジャブ・因果論・量子論」等がある。前者の2つはグラフィカルモデルをベースとしたものとなり、後者の二つは哲学よりの因果とか時間についての概念に対する考察となっている。時間軸を考慮に入れた機械学習は、高度なアプローチの部類であり、現在でも学会で発表されつつあるもので、それらの考え方のベース(アイデアの種)として読むのも良いと思う。

因果に関しては、哲学や禅などでもテーマとして取り上げられている。それらはまた別の機会でも書いてみたい。今回のような統計的アプローチに関しても別の機会に実際のユースケースについてもう少し具体的に述べてみたい。