Artificial Intelligence Technology Web Technology Knowledge Information Processing Technology Semantic Web Technology Ontology Technology Natural Language Processing Machine learning Ontology Matching Technology
Continuing from the previous article on similarity in natural language from ontology matching. In the previous article, I gave an overview of similarity and mentioned that there are two approaches to look at similarity: one that considers only strings, and one that uses some linguistic knowledge to interpret the strings. In this article, we will discuss the method that considers only strings.
String-based methods use the structure of the string (as a sequence of characters). String-based methods usually determine that class Book and Textbook are similar, but not that class Book and Volume are similar.
There are various methods for comparing strings, depending on how the strings are viewed. For example, an exact sequence of letters, an incorrect sequence of letters, a set of letters, or a set of words. (Cohen et al. 2003b) compares various string matching techniques, ranging from distance similarity functions to token-based distance functions. In this section, we discuss the most frequently used techniques.
They include (1) normalization techniques used to reduce the strings to be compared to a common format, (2) substring or subsequence techniques, which seek similarity based on common characters between strings, (3) edit distance, which further evaluates the possibility that one string is an incorrect version of another string, and (4) two statistical measures that establish the importance of words in a string by weighting the relationship between the two strings, and (5) distinguishing path comparisons.
(1) Normalization
Before comparing actual strings that have meaning in natural language, normalization can improve the results of subsequent comparisons. Specifically
(a) In case normalization, each alphabetic character in a string is converted to lowercase. For example, CD becomes cd, and SciFi becomes scifi.
(b) Diacritical suppression replaces characters with diacritical symbols with the most common substitution characters. For example, replace Montréal with Montreal.
Normalize all whitespace characters, such as spaces, tabs, carriage returns, etc., or a sequence of these characters, to a single whitespace character.
(d) Link stripping, which normalizes links between words, such as replacing apostrophes and blank underlines with dashes and blanks. For example, peer-reviewed becomes peer reviewed.
(e) Digit suppression suppresses numbers. For example, book24545-18 becomes book.
(f) Punctuation removal suppresses punctuation. For example, C.D. becomes CD.
There are some limitations to these normalization operations, especially when they are
– They are often language dependent: e.g., they work with Western languages)
– They are order dependent: applying them in any order may not always produce the same result.
– As a result, meaningful information may be lost. For example, carbon-14 becomes carbon, or sentence breaks that are very useful for parsing are lost.
– Variations may be reduced, but synonyms may be increased. For example, the French words livre
and livré would be different words meaning book and delivery, respectively.
(2) String equivalence
String equivalence returns 0 if the target strings are not identical, and 1 if they are identical. This can be seen as a measure of similarity.
Definition 8 (String equality) String equality is the similarity σ : S × S → [0 1] such that ∀x, y ∈ 𝕊, σ (x, x) = 1 and x ≠ y, σ (x, y) = 0.
This can be done after some syntactic normalization, such as string downcasing, encoding conversion, or diacritical marks normalization.
This measure does not describe how the strings differ; a more direct way to compare two strings would be the Hamming distance, which counts the number of parts where the two strings differ (Hamming 1950). Here is one normalized by the length of the longest string.
Definition 9 (Hamming Distance) Hamming distance is the dissimilarity δ : S × S → [0 1] as in the following equation.
\[\delta(s,t)=\frac{\left(\displaystyle \sum_{i=1}^{min(|s|,|t|}s(i)\neq t(i)\right)+||s|-|t||}{max(|s|,|t|)}\]
(3) The substring test
Various variations can be obtained from the equality of strings, for example, if a string is a substring of another string, we consider the strings to be very similar.
Definition 10 (substring test) A substring test is a similarity such that σ:S×S→[01], where σ(x,y) = 1 if there exists p, s ∈ S such that x=p+y+s or y=p+x+s for ∀x, y ∈ S, and σ(x,y) = 0 otherwise.
This is clearly a similarity. This measure can be improved to substring similarity, which measures the ratio of common parts between two strings.
Definition 11 (Similarity of strings) The similarity of strings is the similarity σ : S × S → [0 1]. Let S → [0 1] and let ∀x, y ∈ S, t be the longest common substring of x and y. 𝝈(x, y) = 2|t|/(|x|+|y|)
This measure is indeed similarity. Similarity of substrings can also be considered in the same way. This definition can be used to construct functions based on longest common prefix or longest common suffix.
For example, the similarity between ARTICLE and ARICLE is 8/13=0.61, the similarity between ARTICLE and PAPER is 1/12=0.08, and the similarity between ARTICLE and PARTICLE is 14/15=0.93.
In this model, we can define prefix and suffix pre-similarity from prefix and suffix tests that test whether one string is a prefix or suffix of another string. These measures would not be symmetrical. The prefix and suffix pre-similarity may be useful to test whether one string represents a more general concept than another (in many languages, adding a clause to a term limits its scope). For example, reviewed article is more specific than article. It can also be used to compare strings and similar abbreviations (such as ord and order).
n-gram similarity is another common method used to compare strings. n-gram similarity calculates the number of common n-grams consisting of n characters. For example, the trigrams of the string article are art, rti, tic, icl, cle.
Definition 12 (n-gram similarity) Let ngram(s, n) be the set of substrings of s of length n. An n-gram similarity is a similarity σ : S × S → R such that 𝝈(s, t)=|ngram(s, n) ∩ ngram(t, n)| The normalized version of this function is δ(s, t)=|ngram(s, n) ∩ ngram(t, n)|/(min(|s|-|t|)-n+1)
This function becomes very efficient when only a few letters are missing.
For example, the similarity between article and article is 2/4 = 0.5, and the similarity between article and paper is 0. The similarity between article and particle is 5/6 = 0.83. In order to cope with too small strings, we can add extra characters at the beginning and end of the string to cope with too small strings.
(4) Editing distance
Intuitively, the edit distance between two objects is the minimum cost of the operation applied to the other object to obtain one object. The edit distance will be designed to measure the similarity between strings that may contain spelling errors.
Definition 13 (Editing Distance) Given a set of string operations Op(op : S → S) and a cost function w : Op → R such that for any pair of strings there exists a sequence of operations that transforms the first string into the second string (or vice versa), and for any pair of strings there exists a sequence of operations that transforms the first string into the second string (or vice versa), the editing distance is the dissimilarity δ : S × S → [0 1]. Given a cost function w : Op → R such that there exists a sequence of operations that transforms the first string into the second string (or vice versa) for any pair of strings, the edit distance is the dissimilarityδ : S × S → [0 1], where δ(s, t) is the cost of the less costly sequence of operations that transforms s into t. The equation is the following.
\[ \delta(s,t)=\min_{(op_i)_I;op_n(\dots op_1(s))=t}\left(\displaystyle \sum_{i\in I}w_{op_i}\right) \]
In the string editing distance, the usual operations considered are insertion of a character ins(c,i), substitution of a character sub(c,c′,i), and deletion of a character del(c,i). It is easy to check that these operations are ins(c,i)=del(c,i)-1 and sub(c,c′,i)=sub(c′,c,i)-1. Each operation is assigned a cost, and the distance between the two strings is the sum of the costs of each operation in the set of operations with the lower cost.
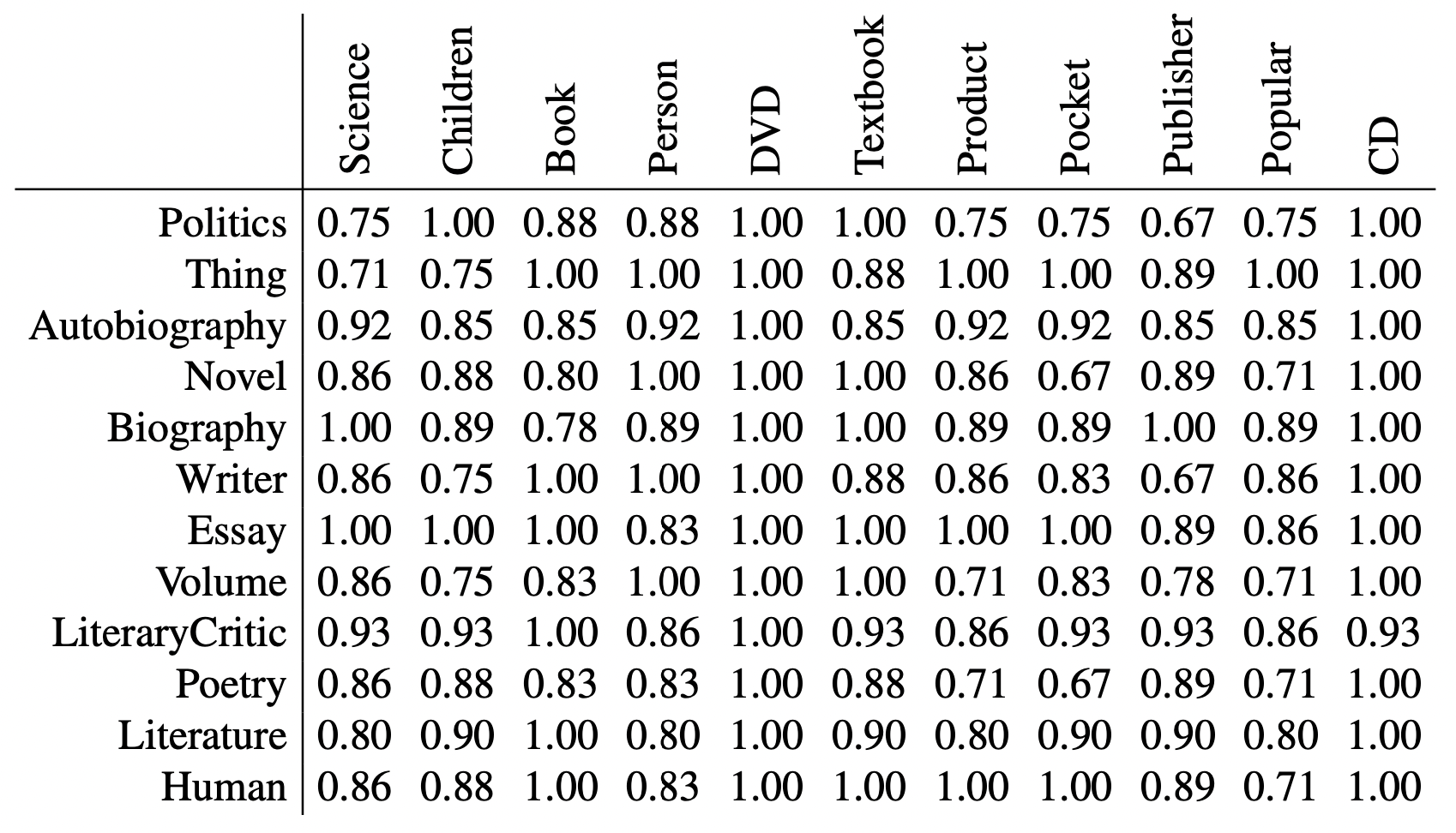
The Levenshtein distance (Levenshtein 1965) is the minimum number of insertions, deletions, and substitutions of characters required to transform one string into another; the Damerau-Levenshtein distance (Damerau 1964) is the minimum number of transposition operations that transpose two adjacent characters into The Damerau-Levenshtein distance (Damerau 1964) adds the transposition operation, which swaps two adjacent letters, with the same weight as the other operations. On the other hand, the Needleman-Wunch distance (Needleman and Wunsch 1970) is an edit distance with a higher cost for ins and del. an example of the Levenstein distance is shown below.

In the example above, the closest names are “Pocket” and “Novel,” “Pocket” and “Poetry,” and “Writer” and “Publisher,” and “Politics” and “Publisher. These names are relatively far from each other (.67). So, in this case, no correspondence can be found using these measures alone. However, if we use the same measure of properties, we can obviously find correspondences between, for example, Author and Author.
Another method is to calculate the cost of an editing operation as a function of the character or substring to which the operation is applied. For this purpose, a cost matrix for each operation is used. A well-known example of such a measure is the Smith-Waterman measure (Smith and Waterman 1981), which is adapted to calculate the distance between biological sequences based on the molecule being manipulated. There are also distance functions such as Gotoh (Gotoh 1981) and Monge-Elkan (Mange and Elkan 1997).
The Jaro measure has been defined for matching proper nouns that may contain similar misspellings (Jaro 1976, 1989). It is based on the number and proximity of common characters between two strings, rather than on an edit distance model. This measure is not symmetric and therefore not a similarity. The Jaro measure is shown below.
Definition 15 (Jaro measure) A Jaro measure is an asymmetric measure σ : S × S → [0 1] such that
For example, comparing article and aricle, and aritcle and paper, the number of common letters is 6, 7, and 1, respectively (in the last case, because the “e” in paper is too far from the “e” in article). The number of transposed common characters will be 0, 1, and 0, respectively. As a result, the similarity of these strings is 0.95, 0.90, and 0.45.
This measure can be improved by prioritizing matches between strings with long common prefixes (Winkler 1999).
Definition 16 (Jaro-Winkler measure) The Jaro-Winkler measure σ : S × S → [0 1] is as follows.
\[\sigma(s,t)=\sigma_{jaro}(s,t)+|pref(s,t)xQx\frac{(1-\sigma_{jaro}(s,t))}{10}\]
where prefix (s, t ) is the longest prefix common to s and t, and Q is a constant.
In this case, the similarity of the three strings compared to the article with Q=4 is .99, .98, and .45. These measures would only be an improvement on the previous measures by explicitly providing a model for mistakes that would make the comparison less penalizing.
A similar measure is SMOA (Stoilos et al. 2005), which is adapted to the way computer users define identifiers. It depends on the length of the common substring and the length of the different substrings, where the second substring is subtracted from the first substring. The value of this scale is between -1 and 1.
(5) Token-based distance
The following methods are derived from information retrieval and consider a string as a set of multiple words (also called a bag of words), i.e., a set in which a particular word may appear multiple times. These methods are usually effective for long texts (consisting of many words). Therefore, it becomes effective to make use of other strings attached to the ontology entities. This can be adapted to ontology entities as follows.
– Aggregating various sources of strings, such as identifiers, labels, comments, and documents. In addition, there are systems that aggregate tokens associated with connected entities (Qu et al. 2006).
– For example, InProceedings becomes In and Proceedings, and peer-reviewed article becomes peer, reviewed and article. (Qu et al. 2006).
Entities in an ontology are identified by a bag (or multiset) of words that are suitable for manipulation using information retrieval techniques. The various similarities and dissimilarities applied to a set of entities can also be applied to these bags of words. For example, the matching coefficient complements the Hamming distance of a set, and the Dice coefficient complements the Hamming distance of a multiset. In other words, the sum, product, and cardinality of multisets are used instead of sets.
The original measures will be based on a corpus of such strings, i.e., the set of all such strings found in one or both ontologies. These measures are no longer specific to the strings being compared, but depend on the corpus.
Usually, we consider a bag of words s as a vector s belonging to a metric space V where each dimension is a term (or token) and each position of the vector is the number of occurrences of the token in the corresponding bag of words. This would be one way to represent multisets. Each document can be thought of as a point in this space identified by a coordinate vector (Salton 1971; Salton and McGill 1983).
Once the entities are transformed into vectors, the usual metric space distances can be used, such as the Euclidean distance, the Manhattan distance (also known as the city block), and any instance of the Minkowski distance. Here, we introduce cosine similarity, which measures the cosine of the angle between two vectors. This is often used for information retrieval.
Definition 17 (Cosine similarity) Given a vector σV : V × V → [0 1] corresponding to two strings s and t in a vector space V, cosine similarity is a function σV : V × V → [0 1] such that
\[\sigma_V(s,t)=\frac{\displaystyle\sum_{i\in|V|}\vec{s_i}x\vec{t_i}}{\sqrt{\sum_{i\in|V|}\vec{s_i}^2x\sum_{i\in|V|}\vec{t_i}^2}}\]
For finer granularity, a reduced space, such as that obtained in correspondence analysis, can be used to handle smaller dimensions, and words with similar meanings can be automatically mapped to the same dimension. A well-known example of such a technique is known as indexing potential meanings using singular value decomposition As described in “Overview of Singular Value Decomposition (SVD) and examples of algorithms and implementations” (Deerwester et al. 1990).
TFIDF (Term frequency-Inverse document fre- quency) (Robertson and Spärck Jones 1976) is used to score the relevance of a term to a document (bag of words) by considering its frequency of occurrence in the corpus. This is a very common measure. It is usually not a measure of similarity, but rather an evaluation of the relevance of a term to a document. Here, it is used to evaluate the relevance of a substring to a string by comparing the frequency of the string in the document with its frequency in the whole corpus.(clojure implementation)
Definition 18 (Term frequency-Inverse document frequency)
Given a corpus C of multisets, we define the following measure.
∀t ∈ S, ∀s ∈ C, tf(t,s)=t#s (termfrequency)
∀t ∈ S, idf(t)=log |{s ∈ C;t ∈ s}| (invertedocumentfrequency)
TFIDF(s, t) = tf (t, s) × idf (t) (TFIDF)
Many systems use measures based on TFIDF. These measures calculate the relevance to the corpus based on TFIDF for each term in the string. Vector space techniques are then used to calculate the distance between two strings. Depending on the space chosen, there are several options: the entire corpus, the union of terms covered by the two strings, or only the intersection of terms in both strings. The most commonly used aggregation method will be cosine similarity.
A further method of looking at the relationship between multisets is the probability distribution approach. This would be represented as a probability distribution when it is possible to establish the relevance of a particular document to a topic (by other methods). A typical example of this approach is the Kullback-Leiber divergence measure (Kullback and Leibler 1951). It calculates the variance between two probability distributions.
Definition 19 (Kullback-Leiber divergence) Given a set of documents D with probability distribution π over a set of topics T, the Kullback-Leiber divergence between two documents e and e′ is as follows.
\[\delta(e,e’)=\displaystyle\sum_{t\in T}\pi(t|e)xlog_2\left(\frac{\pi(t|e)}{\pi(t|e’)}\right)\]
This indicator is sometimes used as a distance, but it is not really symmetric.
(6) Path comparison
Path differences consist of comparing not only the labels of the objects, but also the sequence of labels of the entities to which the labeled objects are related. For example, in the ontology on the left in the figure below, the Science class can be identified by the path Prod- uct:Book:Science.

As a first approximation, these can be thought of as specific ways to aggregate tokens in an ordered fashion. One simple (and only) example is to concatenate all the names of the superclasses of a class and then compare them. This means that the result will depend on the comparison of individual strings that have been aggregated in some way.
Definition 20 (Path Distance) Given two sequences of strings, ⟨si⟩i=1 to n and ⟨s'j⟩j=1 to m, their path distance is defined as follows.
\[\delta(<s_i>_{i=1}^n,<s’_j>_{j=1}^m)=\lambda x\delta'(s_n,s’_m)+(1-\lambda)x\]
For example, the equidistance of strings can be scored as δ′, 0 if the strings are equal, and 0.7 as λ. Then, if we have to compare Product:Book:Science with Book:Essay:Science and Product:Cultural:Book:Science, the distances would be 0.273 and 0.09, respectively.
This measure relies on the similarity between the last elements of each path. This similarity is affected by the λ penalty, while each subsequent step is affected by the λ × (1 – λ)n penalty. In other words, this measure takes into account the prefix, but the effect of the prefix on the result is only to the extent that it becomes smaller as the distance from the end of the sequence increases. Thus, this measure depends on the rank of the elements to be compared in the path. A more accurate but costly measure would be to select the best match among both paths and penalize items that are farther from the end of the path. Another way to take these paths into account would be to simply apply them as distances on a sequence, as described in Valtchev (1999).
Summary on string-based methods
The results of string comparison so far are valid when very similar strings are used to represent the same concept. If synonyms with different structures are used, the similarity will be lower. For example, two very similar strings, such as Inpro- ceedings and proceedings, may represent relatively different concepts, so selecting a pair of strings with low similarity will conversely result in many false positives.
These measures will most likely be used to detect whether two very similar strings are being used. Otherwise, a more reliable source of information must be used for matching.
There are several software packages that calculate the distance between strings. The table below provides a simple comparison of the distances available in four Java packages: SimMet- rics,1 SecondString,2 OntoSim3 and SimPack.4 A comparison of the metrics of the second package can be found in (Cohen et al. 2003b).

We have discussed string-based similarity above. In the next article, we will discuss language-based methods.

コメント