similarity(類似性)の基礎(2)文字列ベースのアプローチ

人工知能技術　ウェブ技術　知識情報処理技術　セマンティックウェブ技術   自然言語処理　機械学習技術 　オントロジー技術　オントロジーマッチング技術

前回に引き続きオントロジーマッチングより自然言語の類似性について。前回は類似性の概要を述べ、類似性を見るアプローチには、文字列のみを考慮する方法と、文字列を解釈するために何らかの言語的知識を用いる方法の2つあることを述べた。今回は、文字列のみを考慮した手法について述べる。

文字列ベースのメソッドは、文字列の構造（文字の並びとして）を利用する。文字列ベースのメソッドでは、通常、クラス Book と Textbook は似ていると判断するが、クラス Book と Volume は似ていないと判断する。
文字列を比較する方法は、文字列の見方によって様々な方法がある。例えば、正確な文字の並び、誤った文字の並び、文字の集合、単語の集合などです。(Cohen et al. 2003b)では，距離類似関数からトークンベースの距離関数まで，様々な文字列照合技術を比較している．ここでは、最も頻繁に使用される手法について述べる。
ここでは、(1)比較する文字列を共通のフォーマットに縮小するために用いられる正規化技術、(2)文字列間の共通の文字に基づいて類似性を求める部分文字列または部分配列技術、(3)ある文字列が別の文字列の誤ったバージョンである可能性をさらに評価する編集距離、(4)2つの文字列の関係に重みをつけることで文字列内の単語の重要性を確立する統計的尺度、(5)パス比較を区別している。

(1)正規化

自然言語で意味を持つ実際の文字列を比較する前に、正規化を行うことで、その後の比較結果を改善することができる。具体的には
(a)大文字小文字の正規化では、文字列中の各アルファベット文字を小文字に変換する。例えば，CD は cd，SciFi は scifi となる。
(b)ジアクリティカルの抑制 ジアクリティカル記号を持つ文字を、最も一般的な置換文字に置き換える。たとえば、Montréal を Montreal に置き換える。
(c)空白の正規化 空白、タブ、キャリッジリターンなどのすべての空白文字、またはこれらの連続した文字を、1 つの空白文字に正規化する。
(d)リンクストリッピングでは、アポストロフェイズやブランクアンダーラインをダッシュやブランクに置き換えるなど、単語間のリンクを正規化する。例えば、peer-reviewed は peer reviewed になる。
(e)ディジットサプレッションは、数字を抑制する。例えば、book24545-18はbookになる。
(f)句読点の除去は、句読点を抑制する。例えばC.D.はCDになる。

これらの正規化操作にはいくつかの制約があり、特に以下のような場合に注意が必要となる。
– 言語に依存していることが多い（例：欧米の言語で動作する)
– 順序に依存している：どの順序で適用しても同じ結果になるとは限らない。
– 結果として、意味のある情報が失われることがある。例えば、炭素14が炭素になったり、構文解析に非常に有用な文の区切りが失われたりする。
– バリエーションは減るが、同義語は増える可能性がある。例えば、フランス語のlivre
とlivréは、それぞれ本と配達を意味する別の単語となる。

(2)文字列の等価性

文字列の等価性は、対象となる文字列が同一でない場合は0を、同一である場合は1を返す。これは、類似性の尺度として捉えることができる。

定義 8 (文字列の等質性) 
文字列の等質性とは，∀x, y∈𝕊, σ (x, x) = 1であり，
x ≠ y, σ (x, y) = 0であるような類似性σ : S × S → [0 1] である。

定義 9 (ハミング距離) 
ハミング距離とは、以下の式のような非類似度δ : S×S→[0 1]である。

定義 10(部分文字列テスト) 
部分文字列テストとは、σ:S×S→[01]で、∀x,y∈Sにおいて、
x=p+y+sまたはy=p+x+sとなるp,s∈Sが存在する場合、σ(x,y)=1、
そうでない場合はσ(x,y)=0となるような相似性のことである。

定義 11 (文字列の類似性) 
文字列の類似性は，類似性σ : S × S → [0 1] である。
S → [0 1] とし、∀x, y∈S, tをxとyの最長の共通部分文字列とする。
　　　　　𝝈(x, y) = 2|t|/(|x|+|y|)

定義 12 (n-gram類似性) 
ngram(s, n)を長さnのsの部分文字列の集合とする。
n-gram類似性は、次のような類似性σ : S × S → Rである。
　　　 𝝈(s, t)=|ngram(s, n) ∩ ngram(t, n)|
この関数の正規化されたバージョンは
  δ(s, t)=|ngram(s, n) ∩ ngram(t, n)|/(min(|s|-|t|)-n+1)

定義 13 (編集距離) 
文字列操作の集合Op(op : S → S)と、文字列の任意のペアに対して、
1番目の文字列を2番目の文字列に変換する操作のシーケンスが存在するような
コスト関数w : Op → Rが与えられ、文字列の任意のペアに対して、
最初の文字列を2番目の文字列に変換する（またはその逆）操作のシーケンスが
存在する場合、編集距離は非類似度δ : S × S → [0 1] であり、δ(s, t)は
sをtに変換するよりコストの低い操作のシーケンスのコストとなる。
式としては以下のものとなる。

定義 15 (Jaro尺度) 
Jaro measureは、以下のような非対称測度σ : S×S→[0 1]である。

定義 16 (Jaro-Winkler尺度) 
Jaro-Winkler measure σ : S × S → [0 1] は次の通りである。

定義 17(コサイン類似度) 
ベクトル空間Vにおける2つの文字列sとtに対応するベクトルσV : V × V → [0 1]を考えると、
cosine similarityは次のような関数σV : V × V → [0 1]である。

定義 18 (Term frequency-Inverse document frequency) 
多重集合のコーパスCが与えられたとき、以下の尺度を定義する。
∀t∈S,∀s∈C, tf(t,s)=t#s (termfrequency) 
∀t∈S, idf(t)=log |{s∈C;t∈s}| (inversedocumentfrequency) 
TFIDF(s, t) = tf (t, s) × idf (t) (TFIDF)

多くのシステムでは、TFIDFに基づいた尺度を使用している。これらの尺度は、文字列の各用語について、TFIDFに基づいてコーパスとの関連性を計算する。そして、2つの文字列の間の距離を計算するために、ベクトル空間技術を使用する。選択された空間に応じて、コーパス全体、2つの文字列でカバーされる用語の結合、または両方の文字列に含まれる用語の交点のみなど、いくつかのオプションがある。最もよく使用される集計方法は、コサイン類似度となる。
更にマルチセット間の関連性を見る手法として確率分布的なアプローチがある。これは、（他の手法で）あるトピックに対する特定の文書の関連性を確立することが可能な場合に確率分布として表されるものとなる。このアプローチの代表的なものとしては、Kullback-Leiber divergence measureがある(Kullback and Leibler 1951)。これは、2つの確率分布の間の分散を計算するものとなる。

定義 19 (Kullback-Leiber divergence) 
トピックの集合Tに対する確率分布πを持つドキュメントの集合Dが与えられたとき、
2つのドキュメントeとe′の間のKullback-Leiber divergenceは次のようになる。

\[\delta(e,e’)=\displaystyle\sum_{t\in T}\pi(t|e)xlog_2\left(\frac{\pi(t|e)}{\pi(t|e’)}\right)\]

この指標は、距離として使われることもあるが、実際には対称ではない。

(6)パス比較

パスの違いは、オブジェクトのラベルだけでなく、ラベルが付いているものが関係しているエンティティのラベルの並びを比較することで構成されている。例えば、下図の左側のオントロジーでは、ScienceクラスはProd- uct:Book:Scienceというパスで識別できる。

第一近似として、これらは順序付けられた方法でトークンを集約する特定の方法と考えることができる。簡単な（そして唯一の）例としては、クラスのスーパークラスの名前をすべて連結してから比較するものがある。つまり、結果は、何らかの方法で集約された個々の文字列の比較に依存しているのものになる。

定義 20 (経路距離) 
2つの文字列の並び、⟨si⟩i=1 to nと⟨s'j⟩j=1 to mが与えられたとき、
それらの経路距離は以下のように定義される。

\[\delta(<s_i>_{i=1}^n,<s’_j>_{j=1}^m)=\lambda x\delta'(s_n,s’_m)+(1-\lambda)x\]

例えば、文字列の等距離をδ′とし、文字列が等しい場合は0、λとして0.7を採点することができる。そうすると、Product:Book:ScienceとBook:Essay:Science、Product:Cultural:Book:Scienceを比較しなければならない場合、その距離はそれぞれ0.273と0.09となる。
この尺度は、各パスの最後の要素間の類似性に依存しています。この類似性は、λペナルティの影響を受けるが、後続の各ステップは、λ×(1 – λ)nペナルティの影響を受ける。つまり、この計測はプレフィックスを考慮しているが、プレフィックスが結果に与える影響は、シーケンスの最後からの距離が長くなるにつれて小さくなる程度に過ぎない。このように、この尺度は、パスの中で比較する要素のランクに依存する。より正確だがコストのかかる測定法では、両方のパスの中で最もマッチしたものを選択し、パスの最後から離れたアイテムにペナルティを課すことになる。これらのパスを考慮に入れる別の方法は、Valtchev (1999)で説明されているように、単純にシーケンス上の距離として適用することになる。

文字列ベースの手法に関するまとめ

これまでの文字列比較の結果は、同じ概念を表すのに非常に似通った文字列が使われている場合に有効になる。構造の異なる同義語が使用されている場合は、類似度が低くなる。例えば、Inpro- ceedingsとproceedingsのように、非常によく似た2つの文字列が、相対的に異なる概念を表すことがあるため、類似度の低い文字列のペアを選択すると、逆に多くの誤検出が発生する。

これらの尺度は、非常に似通った2つの文字列が使用されているかどうかを検出するために使用されることがほとんどになる。そうでなければ、マッチングにはより信頼性の高い情報源を使用しなければならない。
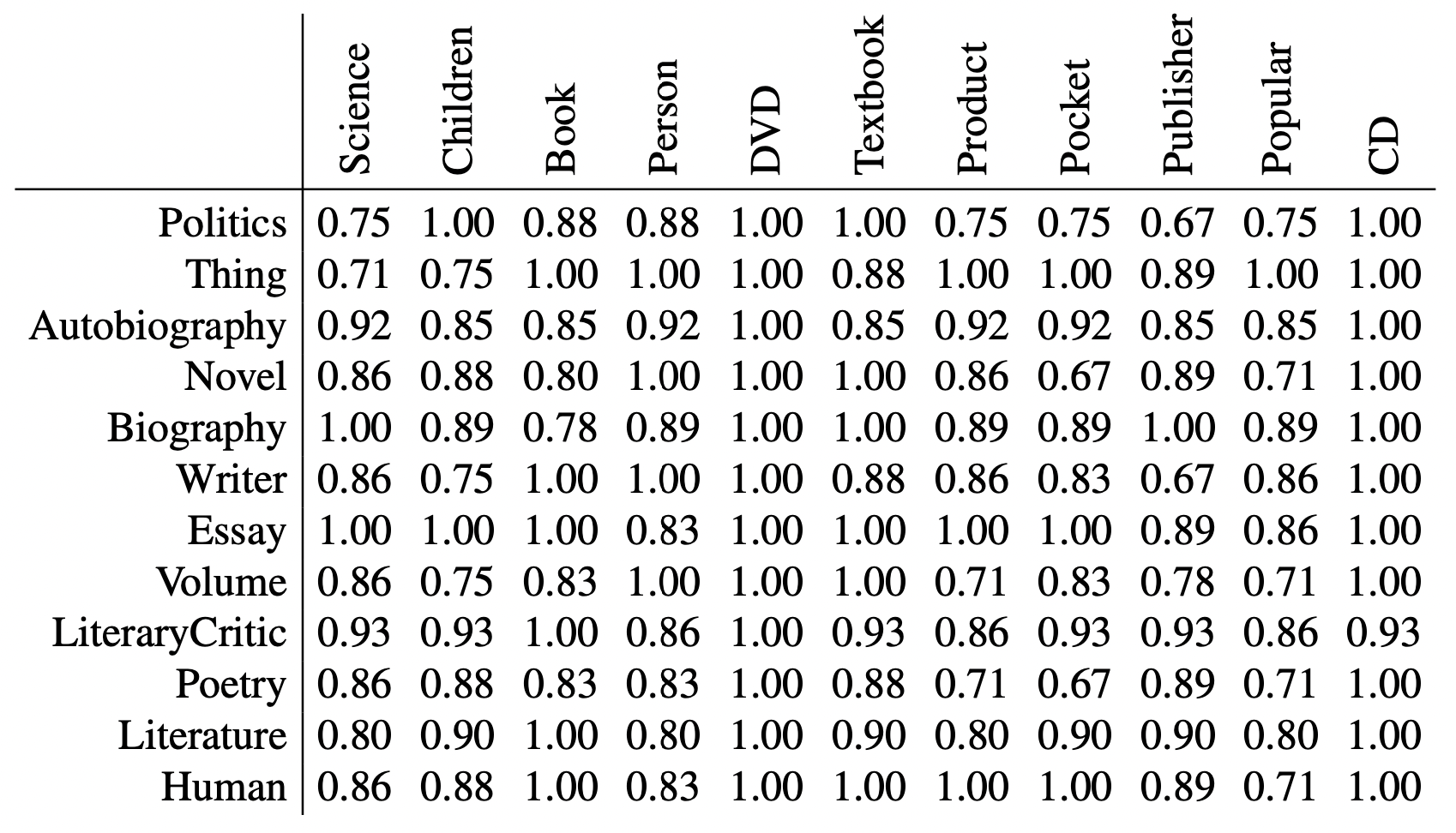
文字列の距離を計算するソフトウェアパッケージはいくつかある。下表は、4つのJavaパッケージで利用可能な距離の簡単な比較となる。SimMet- rics,1 SecondString,2 OntoSim3 and SimPack.4 2番目のパッケージのメトリクスの比較は、(Cohen et al. 2003b)に記載されている。

以上文字列ベースの類似度について述べた。次回は言語ベースの手法について述べる。