Implementation of a simple recommendation algorithm using Clojure(1)
From Clojure for Machine Learning.
A recommender system would be an information system that attempts to predict a user’s preferences and tastes for an item. In recent years, a vast number of recommendation systems have been built in many business and social applications to provide users with a better experience. Such systems can provide useful recommendations to users according to items they have previously rated or liked. Currently, most existing recommendation systems provide users with recommendations about online products, music, and social media. There are also a number of web-based financial and business applications that use recommendation systems.
A recommendation system is an information filtering system that aims to provide users with useful information. A recommendation system uses the user’s behavioral history or recommends what other users like. These two approaches form the basis of the two types of algorithms (content-based filtering and collaborative filtering) used in the recommendation system. Interestingly, some recommendation systems combine these two approaches to make recommendations to users. Both of these techniques are intended to recommend items or domain objects to users that are managed and exchanged in user-centric applications. Such applications include several websites that provide online content and information to users, such as online shopping and media.
In content-based filtering, recommendations are determined by finding similar items using specific user ratings. Each item is represented as a set of discrete features or characteristics, and each item is rated by multiple users. Thus, for each user, there will be multiple sets of input variables representing the characteristics of each item and multiple sets of output variables representing the user’s evaluation of that item. This information can be used to recommend items that have similar features and characteristics to items previously evaluated by a given user.
Collaborative filtering methods are based on collecting data about a particular user’s behavior, activities, or preferences and using this information to recommend items to the user. Recommendations are based on how similar the user’s behavior is to that of other users. In effect, the user’s recommendations are based on past behavior and decisions made by other users in the system. Collaborative filtering techniques use similar user preferences to determine the characteristics of all available items in the system.
Content-based filtering
As mentioned earlier, content-based filtering systems make recommendations to users based on their past behavior as well as the characteristics of items positively rated or liked by a given user. It may also consider items disliked by a given user. Items are generally represented by several discrete attributes. These attributes are similar to input variables or features in machine learning models based on classification or linear regression.
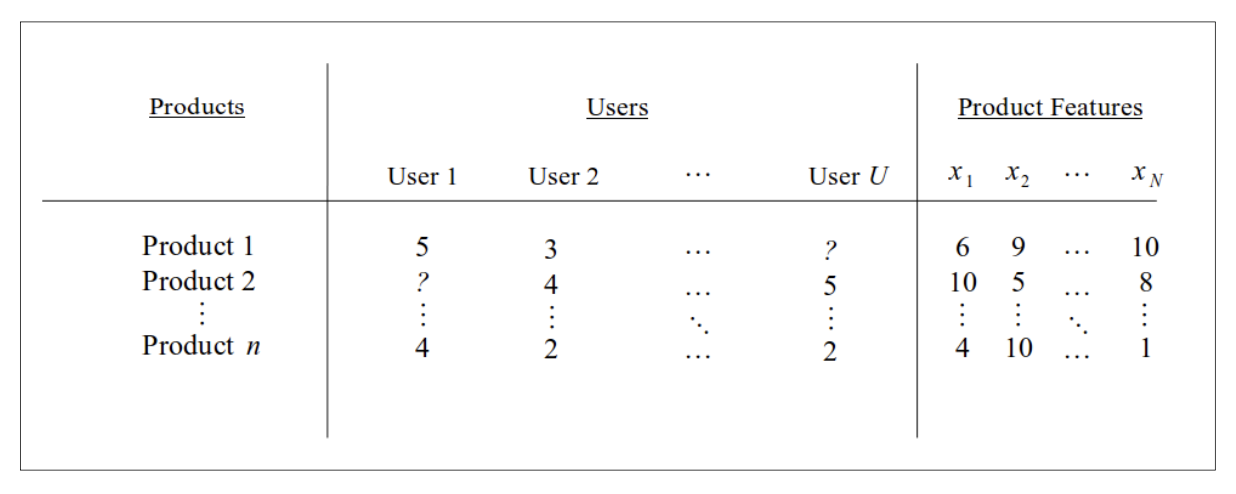
For example, we want to build a system that uses content-based filtering to recommend online products to users. Each product can be characterized and identified by several known features, and the user can provide ratings for each feature of all products. The amount of features of a product has a value between 0 and 10, and the rating that the user provides for a product has a value in the range of 0 to 5. A sample data visualization of this recommendation system in tabular form is shown below.

In the previous table, the system has N products and U users. Each product is defined by N features, each of which will have a value ranging from 0 to 10, and each product is rated by a user. Let Yu,i be the rating of each product i by user u.
and use it to predict the user’s rating. Thus, in content-based filtering, we apply linear regression to each user’s rating and each product’s features to estimate a regression model, which we then use to estimate the user’s rating for the unrated products. In effect, we learn the parameter βμ for all users of the system, using the independent variable Xi and the dependent variable Yu,i. Using the estimated parameter βμ and some given values for the independent variables, we can predict the value of the dependent variable for any given user. Thus, the optimization problem of content-based filtering can be expressed as follows.
\[arg\min_{\beta_u}\left[\displaystyle\sum_{i:r(i,u)=1}\left((\beta_u)^TX_i-Y_{u,i}\right)^2+\frac{\lambda}{2}\sum_{j=1}^n\beta_{u,j}^2\right]\\where\ r(i,u)=1\ if\ user\ u\ has\ rated\ product\ i=0\ otherwise\\and\ \beta_{u,j}\ is\ the\ j^{.th}\ value\ in \ the\ vector\ \beta_u\]
Applying the optimization problem defined in the previous equation to all users of the system, the following optimization problem can be generated for U users
\[arg\min_{\beta_1,\beta_2\dots,\beta_u}\left[\displaystyle\sum_{u=1}^U\sum_{i:r(i,u)=1}\left((\beta_u)^T)X_i-Y_{u,i}\right)^2+\frac{\lambda}{2}\sum_{u=1}^U\sum_{j=1}^n\beta_{u,j}^2\right]\]
Simply put, the parameter vector β attempts to scale or transform the input variables to match the output variables of the model. The second term to be added is for regularization. Interestingly, the optimization problem defined by the regression equation is similar to that of linear regression, and thus content-based filtering can be considered as an extension of linear regression.
A key question for content-based filtering is whether a given recommendation system can learn from user preferences and ratings. One way to provide direct feedback is to ask for ratings of items in the system that the user likes, but these ratings can also be inferred from the user’s past behavior. Also, a content-based filtering system that has been trained for a particular user and a particular category of items cannot be used to predict the same user’s ratings for items in different categories. For example, using one user’s preference for news to predict that user’s preference for online shopping products is a difficult problem.
Collaborative Filtered
The other major recommendation is collaborative filtering, which analyzes data on the behavior of multiple users with similar interests and predicts recommendations for them. The main advantage of this technique is that the system does not depend on the value of the item’s feature variable, and as a result, the system does not need to know the characteristics of the item being offered. The characteristics of the item are determined dynamically from the user’s ratings and the system user’s behavior.
An essential part of the model used in collaborative filtering depends on the behavior of its users. To build this part of the model, the following methods can be used to explicitly determine the user’s ratings for items in the model.
- Ask users to rate items on a specific scale.
- Ask the user to mark items as favorites.
- Present users with a small number of items and ask them to order these items according to their likes and dislikes.
- Ask users to list their favorite items or types of items.
This information can also be gathered implicitly from user behavior. Thus, examples of how to model the behavior of a system’s users for a given set of items or products include the following.
- Observation of items viewed by users.
- Analyze the number of times a particular user has viewed an item.
- Analyze users’ social networks to discover users with similar interests.
For example, consider a recommendation system for the online shopping example described in the previous section. Using collaborative filtering, the system can dynamically determine the feature set of available products and predict the products that would be of interest to the user. Sample data for such a system using collaborative filtering can be visualized using the following table.

With the data in the previous table, product characteristics are unknown. Only the users’ ratings and the users’ behavior models are available data.
The optimization problem for collaborative filtering and product users can be expressed as follows.
\[arg\min_{x_i}\left[\displaystyle\sum_{i:r(i,u)=1}\left((\beta_u)^TX_i-Y_{u,i}\right)^2+\frac{\lambda}{2}\sum_{j=1}^NX_{i,j}^2\right]\\where\ X_{i,j}\ is\ the\ j^{?th}value\ in\ the\ vector\ X_i\]
This equation is considered to be the inverse of the optimization problem defined in content-based filtering. Instead of estimating a vector of parameters βμ, collaborative filtering aims to determine the values of the features of product Xi. Similarly, the optimization problem for multiple users can be defined as follows.
\[arg\min_{X_1,X_2\dots,X_N}\left[\displaystyle\sum_{i=1}^n\sum_{i;r(i,u)=}\left((\beta_u)^TX_i-Y_{u,i}\right)^2+\frac{\lambda}{2}\sum_{i=1}^n\sum_{j=1}^NX_{i,j}^2\right]\]
Using collaborative filtering, we can estimate the product features X1,X 2 , … X N are estimated and these features are used to improve the user β1,β2 ,. . improve the behavior model of βU. The improved user behavior models can then be used to generate better item features again. This process is repeated until the features and the behavior model converge to some appropriate value.
Note that in this process, the algorithm does not need to know the initial feature values of the item; it only needs to estimate the user’s behavior model first to make useful recommendations to the user.
Collaborative filtering can also be combined with content-based filtering in special cases. Such an approach is called a hybrid approach to recommendation. One way to combine the two models is as follows.
- The results of the two models can be weighted and combined numerically.
- Either of the two models can be selected as appropriate at the time.
- Can show the user the combined results of the recommendations from the two models.
Slope One Algorithm
In this section, we describe the Slope One algorithm for collaborative filtering using Clojure.
The Slope One algorithm is one of the simplest forms of item-based collaborative filtering, which is basically a collaborative filtering technique where users explicitly rate their favorite items. In general, item-based collaborative filtering techniques involve estimating a simple regression model for each user using the user’s ratings and the user’s past behavior. Thus, the function fu (x) = ax + b is estimated for all users u in the system.
The Slope One algorithm is less computationally intensive because it models the regression pattern of user behavior using the simpler predictor fu (x) = x + b. The parameter b can be estimated by computing the difference in user ratings between two items; the simplicity of the definition of the Slope One algorithm makes it easy and efficient to implement. Interestingly, this algorithm is less sensitive to overfitting than other collaborative filtering methods.
As an example, consider a simple recommendation system with two items and two users. This sample data can be visualized in the following table.

Using the ratings provided by User 1 in the data in the previous table, we can determine the difference between the ratings for Item A and Item B. This difference is found to be 4-2=2. Therefore, if we add this difference to user 2’s evaluation of item A, we can predict that user 2’s evaluation of item B is 3+2=5.
Let us extend the previous example to three items and three users. This data can be represented as follows.

In this example, the average difference between the ratings of Item A and Item B for User 2 (-1) and User 1 (+2) would be (-1+2) / 2 = 0.5. Thus, on average, Item A is rated 0.5 better than Item B. Similarly, the average difference in rating between Item A and Item C is 3. Since the average difference between user 3’s evaluation of item B and the average evaluation of item A and item B is 2 + 0.5 = 2.5, we can predict user 3’s evaluation of item A.
Implementation with Clojure
We describe a concise implementation of the Slope One algorithm in Clojure. The first step is to define the sample data. This can be done using nested maps, as shown in the following code.Slope One.
(def ? nil)
(def data
{"User 1" {"Item A" 5 "Item B" 3 "Item C" 2 "Item D" ?}
"User 2" {"Item A" 3 "Item B" 4 "Item C" ? "Item D" 4}
"User 3" {"Item A" ? "Item B" 2 "Item C" 5 "Item D" 3}
"User 4" {"Item A" 4 "Item B" ? "Item C" 3 "Item D" ?}})Here, we associate the value nil to the ? symbol with the value nil, which is used to define a nested map data, where each key represents a user and its value represents the user’s evaluation map whose key is the item name. to manipulate the nested map represented by data, several utility methods are Define.
(defn flatten-to-vec [coll]
(reduce #(apply conj %1 %2)
[] coll))The flatten-to-vec function would simply convert the map to a flat vector using the reduce and conj functions. Alternatively, flatten-to-vec can be defined using the functional composition of the standard vec, flatten, and seq functions, as in (def flatten-to-vec (comp vec flatten seq)). Since we are dealing with mappings, the following several functions can be defined to map arbitrary functions to the values of these mappings.
(defn map-vals [f m]
(persistent!
(reduce (fn [m [k v]]
(assoc! m k (f k v)))
(transient m) m)))
(defn map-nested-vals [f m]
(map-vals
(fn [k1 inner-map]
(map-vals
(fn [k2 val] (f [k1 k2] val)) inner-map)) m))The map-vals function can be used to change the values in a given map. It uses the assoc! function to replace the value stored by a given key in the map, and the reduce function to compose and apply the assoc! function to all key/value pairs in the map. In Clojure, most collections containing maps are Note that the transient function, which is persistent and immutable, is used to convert a persistent and immutable map into an immutable map, and the persistent function is used to convert a persistent map into an immutable map. In addition, care must be taken to use the persistent! function to convert transient mutable collections to persistent ones. Separating mutations improves the performance of this function and preserves the immutability guarantee for codes that use this function. The map-nested-vals function defined in the previous code simply applies the map-vals function to the second-level values of the nested map.
To examine the behavior of the map-vals and map-nested-vals functions in the REPL, do the following.
> (map-vals #(inc %2) {:foo 1 :bar 2})
{:foo 2, :bar 3}
> (map-nested-vals (fn [keys v] (inc v)) {:foo {:bar 2}})
{:foo {:bar 3}}As shown in the REPL output, the inc function is applied to the values of map{:foo 1 :bar 2} and {:foo {:bar 3}}. The model is created from the sample data using the Slope One algorithm as follows.
(defn train [data]
(let [diff-map (for [[user preferences] data]
(for [[i u-i] preferences
[j u-j] preferences
:when (and (not= i j)
u-i u-j)]
[[i j] (- u-i u-j)]))
diff-vec (flatten-to-vec diff-map)
update-fn (fn [[freqs-so-far diffs-so-far]
[item-pair diff]]
[(update-in freqs-so-far
item-pair (fnil inc 0))
(update-in diffs-so-far
item-pair (fnil + 0) diff)])
[freqs
total-diffs] (reduce update-fn
[{} {}] diff-vec)
differences (map-nested-vals
(fn [item-pair diff]
(/ diff (get-in freqs item-pair)))
total-diffs)]
{:freqs freqs
:differences differences}))The train function first finds the difference in evaluation of all items in the model with the for macro, and then adds the frequency of evaluation of the items and the difference in evaluation with the update-fn closure. (The main difference between a function and a macro would be that a macro does not evaluate parameters during execution. Also, macros are resolved and expanded at compile time, while functions are called at run time.)
The update-fn function is used to replace key values in the map using the update-in function. care must be taken in the use of the fnil function. This would essentially be a function that checks for the value nil and returns a function that replaces it with a second argument. This is used to process values in nested map data that are represented by a “? symbol whose value is nil. Finally, the train function applies the map-nested-values and get-in functions to the map of valuation differences returned in the previous step. Finally, a map is returned with :freqs and :differences as keys. This map stores the frequencies of items in the model and the differences in their ratings relative to other items, respectively.
This learned model can be used to predict the ratings of items by various users. To do so, the following code implements a function that uses the values returned by the train function defined in the previous code.
(defn predict [{:keys [differences freqs]
:as model}
preferences
item]
(let [get-rating-fn (fn [[num-acc denom-acc]
[i rating]]
(let [freqs-ji (get-in freqs [item i])]
[(+ num-acc
(* (+ (get-in differences [item i])
rating)
freqs-ji))
(+ denom-acc freqs-ji)]))]
(->> preferences
(filter #(not= (first %) item))
(reduce get-rating-fn [0 0])
(apply /))))The predict function uses the get-in function to obtain the sum of the frequency and difference for each item in the map returned by the train function. The function then uses a composite of the reduce function and the / (divide) function to average these evaluated differences. the behavior of the predict function can be examined in the REPL as shown in the code below.
> (def trained-model (train data))
> (predict trained-model {"Item A" 2} "Item B")
3/2As shown in the REPL output, the predict function uses the value returned by the train function to predict the rating of item B by the user who gave item A a rating of 2. The following code wraps the predict function to implement a function that finds the ratings of all items in the model.
(defn mapmap
([vf s]
(mapmap identity vf s))
([kf vf s]
(zipmap (map kf s)
(map vf s))))
(defn known-items [model]
(-> model :differences keys))
(defn predictions
([model preferences]
(predictions
model
preferences
(filter #(not (contains? preferences %))
(known-items model))))
([model preferences items]
(mapmap (partial predict model preferences)
items)))The mapmap function simply applies two functions to the given sequence and returns a map with the key created by the first function kf and the value generated by the second function vf. If only one function is passed, the mapmap function uses the identity function to generate the key for the returned map. The known-items function defined in the previous code uses the keys function to determine all items in the model on the map represented by the :differences key of the value returned by the train function. Finally, the predictions function uses the values returned by the train and known-items functions to determine all items in the model and to predict all unrated items for a particular user. The function also takes an optional third argument, a vector of item names for which it predicts ratings, and returns the predicted values for all items whose names are present in the items vector.
The above behavior is examined in the REPL as follows.
> (known-items trained-model)
("Item D" "Item C" "Item B" "Item A")As you can see in the output, the known-items function returns the names of all items in the model. Next, try the prediction function, which returns the following
> (predictions trained-model {"Item A" 2} ["Item C" "Item D"])
{"Item D" 3, "Item C" 0}
> (predictions trained-model {"Item A" 2})
{"Item B" 3/2, "Item C" 0, "Item D" 3}It should be noted that if the last optional parameter of the predictions function is skipped, the map returned by this function will include all items that have not been previously evaluated by a particular user. This can be asserted in the REPL using the keys function as follows.
> (keys (predictions trained-model {"Item A" 2}))
("Item B" "Item C" "Item D")In the next article, we will describe a recommendation system that uses a measure of similarity between text documents, which is used for clustering text documents using the k-means algorithm.

コメント