Node2Vec
Node2Vec is a graph embedding algorithm reported by Grover et al. in “node2vec: Scalable Feature Learning for Networks” to effectively embed nodes in graph data. Node2Vec is based on ideas similar to DeepWalk, described in “DeepWalk Overview, Algorithms, and Example Implementations,” and uses random walks to learn node embeddings.
In conventional DeepWalk, a sequence of nodes is obtained by depth sampling, but since only a few nodes in the neighborhood of the starting node are sampled, local structure tends to be overlooked, and conversely, if only the neighborhood of the starting node is sampled, global structure tends to be overlooked. On the other hand, sampling only in the neighborhood of the starting node tends to miss the global structure. In contrast, Node2Vec reportedly outperforms existing methods such as DeepWalk in tasks such as multi-label classification and link prediction by combining both types of sampling.
Grover et al. consider neighborhood node sampling as local search and first consider the following two extreme search strategies
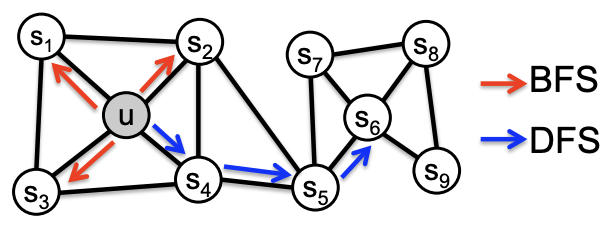
- Breadth First Sampling (BFS): Neighboring nodes are assumed to be directly connected to the starting node by edges.
- Depth First Sampling (DFS): Nearest neighbor nodes are those with increasing distance from the starting node.

Of these, BFS sampling provides embeddings that reflect structural equivalence based on the role of bridges and hubs in the graph. In addition, many nodes are sampled multiple times by BFS, which is expected to reduce the variance of the distribution near the starting node.
When sampling with DFS, a wide range of nodes in the graph can be sampled, and the resulting embedding can reflect the global perspective of the neighborhood and find a community based on homophily. On the other hand, sampling nodes that are too far away from the starting node can lead to cases where the relationship with the starting node becomes tenuous.
Node2Vec introduces p and q as parameters that control the random walk.

In the above figure, the probability of visiting node x next time on a random walk from node t to its neighbor node v is \(\pi_{vx}=\alpha_{pq}(t,x)\cdot \omega_{vx}\) represents the weight of the edge between node v and x, and \(\alpha_{pq}(t,x)\) is the following value.
\begin{eqnarray}\alpha_{pq}(t,x)=\begin{cases}\frac{1}{p}\quad &(d_{tx}=0\ Case)&\\1\quad&(d_{tx}=1\ Case)&\\\frac{1}{q}\quad&(d_{tx}=2\ Case)&\end{cases}\end{eqnarray}
In this case, \(d_{tx}\) denotes the shortest path length between node t and x. The parameter p represents the degree to which a random walk immediately returns to the original node, and the parameter q represents the degree to which a random walk visits distant nodes. If q is small, there is a bias toward nodes further away from the starting node t, resulting in a behavior closer to DFS.
By making \(\pi_{vx}\) a function of the previous node t, we can make the random walk a second-order Markov chain (a stochastic process that depends on the history of the two previous nodes). These innovations make Node2Vec more efficient than pure BFS or DFS in terms of time and space during the computation, and even more efficient by reusing samples.
“node2vec: Scalable Feature Learning for Networks” visualizes how changing the p and q parameters in a network representing the co-occurrence of characters in Les Miserable changes the reflection of similarity and structural equivalence in the embedding of the results. The results are shown in the following figure.

The authors have also experimented with multi-label classification and link prediction on datasets such as BlogCatalog, PPI, and Wikipedia, and have shown that it is more powerful than DeepWalk and LINE described in “Overview, Algorithm and Implementation of LINE (Large-scale Information Network Embedding)“.
Code samples are available at the authors’ public site.
Example implementation of Node2Vec
An example implementation of Node2Vec is shown below. to implement Node2Vec, use Python and perform the following steps.
- Install the necessary libraries. networkx, gensim, and other libraries are required to implement Node2Vec.
pip install networkx gensim- Read the graph data; Node2Vec needs to read the graph data first in order to learn node embedding on the graph. The following is a simple example.
import networkx as nx
# Load graphs (e.g., edge_list.txt)
G = nx.read_edgelist("edge_list.txt", create_using=nx.Graph())- Implement the Node2Vec algorithm. The following is a basic implementation of Node2Vec.
from node2vec import Node2Vec
# Node2Vec Settings
node2vec = Node2Vec(G, dimensions=64, walk_length=30, num_walks=200, p=1.0, q=1.0, workers=4)
# Random walk and embedding learning
model = node2vec.fit(window=10, min_count=1, batch_words=4)
# Get node embedding
node_embeddings = {node: model.wv[node] for node in G.nodes()}- The embedding vectors of nodes are used and applied to a variety of tasks. Examples would be node similarity computation, clustering, classification, link prediction, etc.
This code is an example of a basic implementation of Node2Vec and should be adjusted for specific data sets and tasks. In addition, the adjustment of hyperparameters (embedding dimension, walk length, number of walks, bias parameters p and q, etc.) is important depending on the task.
Node2Vec can also be easily implemented using node2vec, a Python library. node2vec library provides the basic functionality of Node2Vec and is a useful tool for learning to embed in graph data.
Challenges of Node2Vec
Node2Vec is a powerful graph embedding algorithm, but there are some challenges and limitations. The main challenges of Node2Vec are described below.
1. computational cost of random walks:
Random walks are computationally expensive for large graphs because of the search in the graph. In particular, increasing the number of walks or the length of the walk increases the computation time.
2. hyperparameter tuning:
There are several hyperparameters in Node2Vec that need to be tuned appropriately. For example, walk length, number of walks, bias parameters (p and q), number of embedded dimensions, etc. The appropriate hyperparameter settings depend on the task and data.
3. support for non-homogeneous graphs:
Node2Vec is designed for homogeneous graphs (graphs with a single node type and edge type) and is difficult to apply to non-homogeneous graphs (graphs with multiple node types and edge types). Non-homogeneous graphs require appropriate bias control for different node types and edge types.
4. scalability:
Application of Node2Vec to large graphs will cause memory and computational resource constraints. In particular, scalability issues arise when using large embedded dimensions.
5. constraints for static graphs:
Node2Vec is designed for static graphs and is difficult to apply to dynamic graph data. This is because it is difficult to deal with changes in the graph over time.
Despite these challenges, Node2Vec is useful for many graph data-related tasks and is widely used in real-world data analysis and applications. Strategies for addressing the challenges depend on the specific situation, but may include tuning hyperparameters, distributed processing to improve scalability, extensions to non-homogeneous graphs, and application to dynamic graph data.
How Node2Vec Addresses the Challenges
To address the challenges of Node2Vec, the following measures can be considered
1. addressing the computational cost of random walks:
- Graph sampling: to reduce computational cost for large graphs, random walks can be restricted to subgraphs. This allows embeddings to be learned on a subset of the graph rather than the entire graph.
- Distributed Processing: Large graphs can be handled by parallelizing the computation using a distributed processing framework (e.g., Apache Spark). See “Parallel and Distributed Processing in Machine Learning” for more details.
2. dealing with hyperparameter tuning:
- Automatic Tuning of Hyperparameters: Use hyperparameter optimization tools to automatically tune hyperparameters (walk length, number of walks, p, q, number of embedded dimensions, etc.) and take advantage of methods such as Bayesian optimization and grid search. (See “Implementing Bayesian Optimization Tools with Clojure” for details.
3. dealing with non-homogeneous graphs:
- Use extended methods: Use extended versions of Node2Vec and other algorithms to deal with non-homogeneous graphs.Metapath2Vec described in “Overview of Metapath2Vec and examples of algorithms and implementations” and HIN2Vec described in “HIN2Vec Overview, Algorithm and Implementation Examples” .
4. Addressing Scalability:
- Mini-batch learning: Implement mini-batch learning described in “Overview of mini-batch learning and examples of algorithms and implementations” to control memory usage and make it applicable to large graphs. Large data sets can be sampled and trained. For details, see “Convolutional Neural Networks (1) Forward and Backward Propagation Algorithms and Mini-batch” etc.
- Reduction of high-dimensional embeddings: Reducing the number of embedding dimensions can reduce memory usage. However, low-dimensional embedding may cause information loss, so it should be chosen carefully. For more information, please refer to the “High-Dimensional Data” section. For details, see “Plotting high-dimensional data in low dimensions using dimension reduction techniques (e.g., t-SNE, UMAP) to facilitate visualization” etc.
5. dealing with dynamic graph data
- Use dynamic graph embedding algorithms: If the graph changes over time, use dynamic graph embedding algorithms (e.g., DynGEM, time-dependent versions of GraphSAGE) to generate time-aware embeddings. See “Overview of GraphSAGE, Algorithms, and Examples of Implementations. Algorithms and Examples of Implementations” for more information.
Reference Information and Reference Books
For more information on graph data, see “Graph Data Processing Algorithms and Applications to Machine Learning/Artificial Intelligence Tasks. Also see “Knowledge Information Processing Techniques” for details specific to knowledge graphs. For more information on deep learning in general, see “About Deep Learning.
Reference book is

“Graph Neural Networks: Foundations, Frontiers, and Applications“等がある。

“Introduction to Graph Neural Networks“

“Graph Neural Networks in Action“


コメント