Node2Vecの概要とアルゴリズム及び実装例について

機械学習自然言語処理人工知能デジタルトランスフォーメーションセマンティックウェブ知識情報処理グラフデータアルゴリズム関係データ学習推薦技術異常検知・変化検知技術時系列データ解析 python グラフニューラルネットワーク本ブログのナビ

Node2Vecについて

Node2VecはGroverらによって”node2vec: Scalable Feature Learning for Networks“で報告された、グラフデータのノードを効果的に埋め込むためのグラフエンべディングアルゴリズムの一つとなる。Node2Vecは、”DeepWalkの概要とアルゴリズム及び実装例について“で述べられているDeepWalkと似たようなアイデアに基づいており、ノードの埋め込みを学習するためにランダムウォークを使用するものとなる。

従来のDeepWalkでは深さサンプリングによってノード列を得ていたが、出発ノードの近傍のノードは少ししかサンプリングされないため、局所的な構造が見落とされがちで、逆に、出発ノードの近傍だけをサンプリングするのでは、大局的な構造が見落とされがちとなる課題を持っていた。これに対して、Node2Vecは両者を組み合わせたサンプリングにより、多ラベル分類やリンク予測などのタスクにおいてDeepWalkなどの既存手法を上回る性能が出たと報告されている。

Groverらは近傍ノードのサンプリングを局所的な探索とみなし、まず以下の2つの極端な探索戦略について検討している。

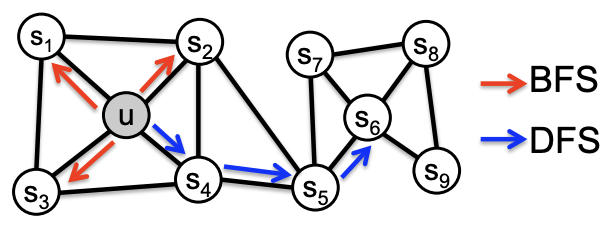
幅優先探索(Breadth First Sampling, BFS): 近傍ノードは出発ノードとエッジで直接結ばれているものにする。
深さ優先探索(Depth First Sampling, DFS): 近傍ノードは出発ノードからの距離が増えていくものからなる。

このうち、BFSでサンプリングすることで、ブリッジやハブなどのグラフ上の役割に基づく構造同値(structural equivalence)を反映したエンべディングがえられる。また、BFSによって多くのノードが複数回サンプリングされ、それによって出発ノード近傍の分布の分散も減る効果が見込まれる。

DFSでサンプリングすると、グラフの広い範囲のノードをサンプリングでき、得られるエンべディングに対して、近傍の大局的な視点を反映させることができ、同類性(homophily)に基づくコミュニティを見出すことができる。その反面、出発ノードから距離が大きすぎるノードをサンプリングすると、出発ノードとの関係性が希薄になるというケースが起きる。

Node2Vecでは、ランダムウォークを制御するパラメータとしてpとqを導入する。

上図において、ノードtから隣接ノードvにランダムウォークしたときに、次にノードxを訪れる確率を\(\pi_{vx}=\alpha_{pq}(t,x)\cdot \omega_{vx}\)とする。\(\omega_{vx}\)はノードvとxの間のエッジの重みを表し、\(\alpha_{pq}(t,x)\)は以下の値とする。

\begin{eqnarray}\alpha_{pq}(t,x)=\begin{cases}\frac{1}{p}\quad &(d_{tx}=0の場合)&\\1\quad&(d_{tx}=1の場合)&\\\frac{1}{q}\quad&(d_{tx}=2の場合)&\end{cases}\end{eqnarray}

このとき、\(d_{tx}\)はノードtとxとの最短パス長を示す。パラメータpはランダムウォークですぐ元のノードに戻る度合いを表し、パラメータqはランダムウォークで離れたノードを訪れる度合いを表している。pの値が小さければ、一度訪れたノードtに戻る確率が高くなり、ランダムウォークが局所的となりBFSとなる。qの値が小さければ、出発ノードtからより離れたノードへのバイアスがかかりDFSに近い振る舞いとなる。

これに\(\pi_{vx}\)をひとつ前のノードtの関数とすることで、ランダムウォークを2次のマルコフ連鎖(過去の2つのノードの履歴に依存して決まる確率過程)とすることができる。これらの工夫により、純粋なBFSやDFSと比べて、計算の際の時間面や空間面での効率を高め、サンプルを再利用することでさらに効率を高めることがNode2Vecの特徴となる。

“node2vec: Scalable Feature Learning for Networks“では、Les Miserableの登場人物の共起を表すネットワークでpとqのパラメータを変えた時に結果のエンべディングでの同類性と構造同値の反映がどう変わるかを可視化している。

また、BlogCatalog、PPI、Wikipediaなどのデータセットで多ラベル分類やリンク予測の実験を行いDeepWalkや”LINE（Large-scale Information Network Embedding）の概要とアルゴリズム及び実装例について“で述べているLINEと比較して高性能であることを提示している。

コードサンプルは筆者らの公開サイトにて入手することができる。

Node2Vecの実装例について

Node2Vecの実装例を示す。Node2Vecを実装するには、Pythonを使用し、以下のステップを実行する。

必要なライブラリをインストールする。Node2Vecを実装するためには、networkx、gensimなどのライブラリが必要となる。

pip install networkx gensim

グラフデータを読み込む。Node2Vecは、グラフ上でのノード埋め込みを学習するため、まずはグラフデータを読み込む必要がある。以下は、簡単な例となる。

import networkx as nx

# グラフの読み込み（例: edge_list.txt）
G = nx.read_edgelist("edge_list.txt", create_using=nx.Graph())

Node2Vecアルゴリズムを実装する。以下は、Node2Vecの基本的な実装例となる。

from node2vec import Node2Vec

# Node2Vecの設定
node2vec = Node2Vec(G, dimensions=64, walk_length=30, num_walks=200, p=1.0, q=1.0, workers=4)

# ランダムウォークと埋め込みの学習
model = node2vec.fit(window=10, min_count=1, batch_words=4)

# ノードの埋め込みを取得
node_embeddings = {node: model.wv[node] for node in G.nodes()}

ノードの埋め込みベクトルを使用して、さまざまなタスクに適用する。たとえば、ノードの類似性計算、クラスタリング、分類、リンク予測などとなる。

このコードは、Node2Vecの基本的な実装の一例であり、具体的なデータセットやタスクに合わせて調整する必要がある。また、ハイパーパラメータ（埋め込み次元、ウォークの長さ、ウォークの回数、バイアスパラメータpとqなど）の調整がタスクに応じて重要となる。

また、Node2Vecは、Pythonのライブラリであるnode2vecを使用することで、簡単に実装できます。node2vecライブラリは、Node2Vecの基本的な機能を提供し、グラフデータに埋め込みを学習するための便利なツールとなる。

Node2Vecの課題について

Node2Vecは強力なグラフ埋め込みアルゴリズムだが、いくつかの課題や制約も存在する。以下に、Node2Vecの主な課題について述べる。

1. ランダムウォークの計算コスト:

ランダムウォークは、グラフ内の探索を行うため、大規模なグラフに対して計算コストが高くなる。特に、ウォークの回数やウォークの長さを増やすと、計算時間が増加する。

2. ハイパーパラメータの調整:

Node2Vecにはいくつかのハイパーパラメータが存在し、それらを適切に調整する必要がある。例えば、ウォークの長さ、ウォークの回数、バイアスパラメータ（pとq）、埋め込み次元数などで、適切なハイパーパラメータの設定は、タスクやデータに依存する。

3. 非同次グラフへの対応:

Node2Vecは同次グラフ（単一のノードタイプとエッジタイプを持つグラフ）に対して設計されており、非同次グラフ（複数のノードタイプやエッジタイプを持つグラフ）に適用するのは難しい。非同次グラフでは、異なるノードタイプやエッジタイプに対する適切なバイアス制御が必要となる。

4. スケーラビリティ:

大規模なグラフに対してNode2Vecを適用すると、メモリや計算リソースの制約が発生する。特に、大規模な埋め込み次元を使用する場合、スケーラビリティの課題が生じる。

5. 静的なグラフに対する制約:

Node2Vecは静的なグラフに対して設計されており、動的なグラフデータに適用するのは難しい。これは時間経過に伴うグラフの変化に対処することが難しいからである。

これらの課題にもかかわらず、Node2Vecは多くのグラフデータ関連タスクで有用であり、実世界のデータ解析や応用で広く使用されている。課題への対処策は、具体的な状況に応じて異なりますが、ハイパーパラメータのチューニング、スケーラビリティ向上のための分散処理、非同次グラフに対する拡張、動的なグラフデータへの適用などが考えられる。

Node2Vecの課題への対応策について

Node2Vecの課題に対処するために、以下の対応策が考えられる。

1. ランダムウォークの計算コストへの対処:

グラフサンプリング: 大規模なグラフに対して計算コストを削減するために、ランダムウォークをサブグラフに制限して実行することができる。これにより、全体のグラフではなくサブセットのグラフで埋め込みを学習可能となる。
分散処理: 分散処理フレームワーク（例：Apache Spark）を使用して、計算を並列化することで、大規模なグラフに対応できる。詳細は”機械学習における並列分散処理“を参照のこと。

2. ハイパーパラメータの調整への対処:

ハイパーパラメータの自動チューニング: ハイパーパラメータ（ウォークの長さ、ウォークの回数、p、q、埋め込み次元数など）を自動的に調整するハイパーパラメータ最適化ツールを使用し、ベイズ最適化やグリッドサーチなどの手法を活用できる。詳細は”Clojureを用いたベイズ最適化ツールの実装“を参照のこと

3. 非同次グラフへの対応への対処:

拡張手法の利用: 非同次グラフに対処するために、Node2Vecの拡張バージョンや他のアルゴリズムを使用する。Metapath2VecやHIN2Vecなどのアルゴリズムは、複数のノードタイプやエッジタイプを考慮に入れるために使用されます。詳細は”Metapath2VecやHIN2Vecについて“を参照のこと。

4. スケーラビリティへの対処:

ミニバッチ学習: ミニバッチ学習を導入して、メモリ使用量を制御し、大規模なグラフに適用可能にする。大規模なデータセットをサンプリングして学習することができる。詳細は“畳み込みニューラルネットワーク(1)順伝搬と逆伝搬アルゴリズムとミニバッチ“等を参照のこと。
高次元埋め込みの削減: 埋め込み次元数を削減することで、メモリ使用量を削減できます。ただし、低次元の埋め込みは情報損失を招く可能性があるため、慎重に選択する必要があ.る。詳細は”高次元のデータを次元削減技術（例: t-SNE、UMAP）を使用して低次元にプロットし、可視化を容易にする手法について“等を参照のこと。

5. 動的なグラフデータへの対処:

動的グラフ埋め込みアルゴリズムの使用: グラフが時間経過に伴って変化する場合、動的グラフ埋め込みアルゴリズム（例：DynGEM、GraphSAGEの時間依存バージョン）を使用して、時間に対応した埋め込みを生成する。詳細は”GraphSAGEの概要とアルゴリズム及び実装例について“を参照のこと。