機械学習技術 人工知能技術 デジタルトランスフォーメーション技術 確率的生成モデル 本ブログのナビ 深層学習技術 ノンパラメトリックベイズとガウス過程 サポートベクトルマシン Clojureと関数プログラミング
サマリー
ベイズ最適化(bayesian optimization)は、少数標本と最低限の過程に基づいて確率的な予測を行うことのできる、ガウス回帰過程の特徴をフル活用した応用技術となる。
ベイズ最適化とは
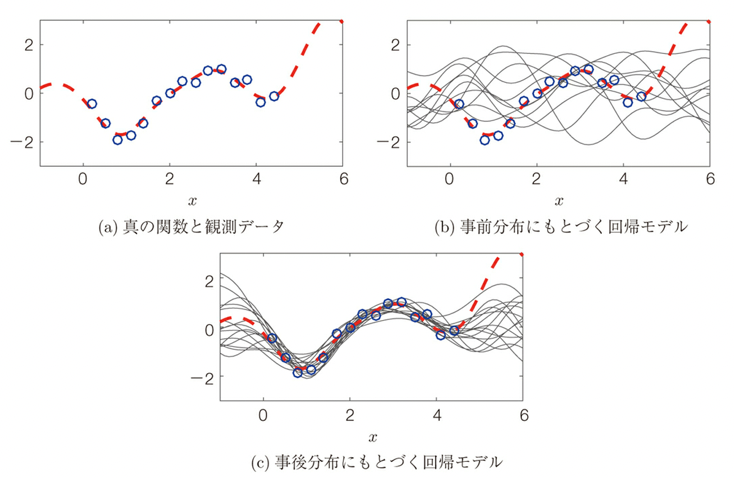
ガウス過程は以前”ガウス過程雑記 – 関数の雲の利点と回帰モデルとカーネル法そして物理的モデルとの関係“で述べたように入力xと出力yの間の関数関係(赤点線)と、その一部に関する観測データ(青丸印)が得られているとき、この関数関係をガウス過程を使うと以下のように表され、事前分布ではランダムな雲のような分布が実データが与えられると収束していく過程を表したものであり

ベイズ最適化は、”ガウス過程の空間統計学、ベイズ最適化への適用”で述べているようにガウス過程の解析で求められた事後確率の期待値と分散を組み合わせた獲得関数と期待改善度関数を最適化する(最適化の戦略としては”UCB(Upper Confidence Bound)アルゴリズムの概要と実装例“で述べているUpper Confidence Bound(上側信頼限界)UCB戦略を用いる)ことでこの収束を効果的に行うものとなる。実際の最適化は以下の図のように、実データから生成されたガウス過程の予測関数の分散の多い(と期待値から求められた)ポイント(下図での紫の幅の広いところ)を次の測定点として選び、その結果を反映して次の予測関数を求め、さらに分散の多い(と期待値から求められた)ポイントを選びながら予測関数を収束させていくものとなる。

このような手法に似た既存のものとしては、実験計画法(experimental design)と呼ばれる手法がある。実験計画法は離散的なデータを用いて、ベイズ最適化と同様にバラツキ(誤差)に注目して最適なパラメータを選んでいくものとなるが、ベイズ最適化のアプローチは連続値や分散/期待値による最適化など使うことができ、より汎用的に利用できるアフーローチとなる。
具体的な例としては、医療や化学/材料研究等の実験計画において、実験を行いながら逐次的に次に行うべき実験パラメータの最適な組み合わせを抽出したり、機械学習におけるハイパーパラメータの学習/評価のサイクルを回しながら逐次的に最適化を行ったり、製造業での部品のすり合わせによる機能の最適化に用いられたりと広範囲に利用できる技術となる。
pythonのコードでは以前”GPy – Pythonを用いたガウス過程のフレームワーク”で紹介したシェフィールド大学によるGPyをベースとしたライブラリGPyOptやTensorflowやPyTorchを用いたGPFlowやGPyTorch、あるいはMATLABではStastics and Machine Learning Tollbox(有料)の一部としてベイズ最適化を行う関数bayesoptが実装されているものが著名なものとなる。
今回は、Clojureの数学ライブラリであるfastmathを利用したClojureでのベイズ最適化について述べる。
Clojureでの実装
Clojureでの実装は、fastmath, cljplot等の統計的機械学習のツールを多数アップしているgenerateme氏のBayesian Optimizationの記事とfastmathライブラリを参照/利用した。fastmathに関する記事は”Clojureでのガウス過程の実装“を参照のこと
まずプロジェクトファイルはいつものように”lein new bo-test(任意のファイル名)”で作成する。prject.cljファイルは以下のようにする。
(defproject bo-test2 "0.1.0-SNAPSHOT"
:description "FIXME: write description"
:url "http://example.com/FIXME"
:license {:name "EPL-2.0 OR GPL-2.0-or-later WITH Classpath-exception-2.0"
:url "https://www.eclipse.org/legal/epl-2.0/"}
:dependencies [[org.clojure/clojure "1.10.1"]
[generateme/fastmath "1.4.0-SNAPSHOT"]
[cljplot "0.0.2-SNAPSHOT"]
[clojure2d "1.2.0-SNAPSHOT"] ]
:repl-options {:init-ns bo-test2.core})ここで注意すべきは、fastmathは現在”2.1.8″まで進んでいるが、ベースとなっているSMILE 2.x API の大幅な変更により、関数の定義等大きく変わってしまっている為、”1.4.0-SNAPSHOT”をそのまま利用する必要があることである。
src/bo_test/core.cljのファイルのnamespaceとライブラリ導入部分は以下のようになる。
(ns bo-test2.core)
(require '[cljplot.build :as b]
'[cljplot.core :refer :all]
'[fastmath.core :as m]
'[fastmath.kernel :as k]
'[fastmath.random :as r]
'[fastmath.optimization :as o]
'[fastmath.classification :as cl]
'[clojure2d.color :as c]
'[clojure.java.io :as io]
'[clojure.string :as str])最適化
ここで最適化について少し述べる。最適化の最もシンプルな形はある関数(ブラックボックス関数)が与えられた時に、解析的ではない手法でその関数の最適値を求めるものとなる。JavaやPyhtonの数学ライブリラリーでそのような最適化に対して、様々なクラス(関数)を持つ。
例として以下のような複雑なブラックボックス関数を考える。
\[z=1+\left(\left(\frac{sin(2xy)}{xy}\right)+sin(x+y)+cos(y+y)+sin(2xy))\right)\]

これに対して最適化アルゴリズムの一つであるBOBYQAを用いてJavaの数学ライブラリであるfastmathのクラスの一つであるoptimizerのラッパーを使って、特定の境界領域(bouns2)内での最適化を行うと以下のようになる。
(defn black-box-function
^double [^double x ^double y]
(+ 1.0 (* (m/sinc (+ 2.0 x y))
(m/sin (+ x x))
(m/cos (+ y y))
(m/sin (* 2.0 x y)))))
(black-box-function -1.5 0.5) ;; 1.0
(def bounds2 [[-1.0 0.5] [-2 -0.5]])
(o/maximize :bobyqa black-box-function2 {:bounds bounds2}) ;;[(-0.601666316911455 -1.4622938217249408) 1.8891426447312971]これに対して、ベイズ最適化を行うと以下のようになる。
(def bo (o/bayesian-optimization black-box-function2 {:bounds bounds2}))
(first bo) ;; {:x [-0.5818284049054684 -1.7214731540148598], :y 1.6810441771166404,...
(select-keys (nth bo 25) [:x :y]) ;; {:x (-0.6014301541014717 -1.4624072382800395), :y 1.8891423521925965}
(def palette (reverse (:rdylbu-9 c/palette-presets)))
(def gradient (c/gradient palette))
(defn draw-2d
[f bounds bayesian-optimizer iteration]
(let [{:keys [util-fn gp xs]} (nth bayesian-optimizer iteration)
cfg {:x (first bounds)
:y (second bounds)
:palette palette
:contours 30
:gradient gradient}]
(xy-chart {:width 700 :height 700}
(b/series [:contour-2d f (assoc cfg :position [0 1])]
[:scatter xs {:size 10
:color (c/darken (first palette))
:margins {:x [0 0] :y [0 0]}
:position [0 1]
:label "2d function with guessed points."}]
[:function-2d util-fn (assoc cfg :position [0 0]
:label "Utility function")]
[:contour-2d (fn [x y] (gp [x y]))
(assoc cfg :position [1 1]
:label "Gaussian processes - mean (interpolation)")]
[:contour-2d (fn [x y] (second (gp [x y] true)))
(assoc cfg :position [1 0]
:label "Gaussian processes - std dev")])
(b/add-axes :bottom)
(b/add-axes :left))))
(def draw-black-box2 (partial draw-2d black-box-function2 bounds2))
(save (draw-black-box2 bo 0) "results/black-box2.jpg")ベイズ最適化(bo)のステップを増やしていくと、最適値に収束していくことが確認できる。

ここで最適化の戦略としてUCBを用いたものは以下ようになる。
(def bo (o/bayesian-optimization black-box-function2 {:bounds bounds2
:noise 0.01
:utility-function-type :ucb
:utility-param 0.1}))
(save (draw-black-box2 bo 15) "results/black-box2-ucb-low.jpg") 
また最適化戦略としてeiを用いたものは以下のようになる。
(def bo (o/bayesian-optimization black-box-function2 {:bounds bounds2
:noise 0.01
:utility-function-type :ei
:utility-param 0.01}))
(save (draw-black-box2 bo 15) "results/black-box2-ei-low.jpg")
さらに、カーネル関数をMatternにしたものは以下のようになる。
(def bo (o/bayesian-optimization black-box-function2 {:bounds bounds2
:utility-function-type :ei
:kernel (k/kernel :mattern-12 2)
:noise 0.1}))
(save (draw-black-box2 bo 15) "/results/black-box2-wide.jpg")
ベイジアン最適化では利用できるパラメータが多々あり、それらの最適化により収束の様子が異なってくる。
最適化に関してはRのoptimxパッケージを用いると、各種最適化の比較も可能となる。
library(optimx)
loglik <- function(x, param) {
-sum(dnbinom(x, size = param[1], mu = param[2], log = TRUE))
}
set.seed(71)
data <- rnbinom(500, size = 10, mu = 5)
initparam <- c(10, 5)
optimx(par = initparam, fn = loglik, x = data, control = list(all.methods = TRUE))
p1 p2 value fevals gevals niter convcode kkt1 kkt2 xtimes
BFGS 9.889487 5.038007 1.190725e+03 14 5 NA 0 NA NA 0.01
CG 9.892441 5.037995 1.190725e+03 305 101 NA 1 NA NA 0.27
Nelder-Mead 9.892127 5.038049 1.190725e+03 41 NA NA 0 NA NA 0.02
L-BFGS-B 9.889511 5.038000 1.190725e+03 13 13 NA 0 NA NA 0.03
nlm 9.889480 5.037999 1.190725e+03 NA NA 11 0 NA NA 0.01
nlminb 9.889512 5.038000 1.190725e+03 8 18 5 0 NA NA 0.00
spg 9.889768 5.038000 1.190725e+03 24 NA 18 0 NA NA 0.13
ucminf 9.889507 5.037997 1.190725e+03 9 9 NA 0 NA NA 0.02
Rcgmin NA NA 8.988466e+307 NA NA NA 9999 NA NA 0.00
Rvmmin NA NA 8.988466e+307 NA NA NA 9999 NA NA 0.00
newuoa 9.889511 5.038000 1.190725e+03 34 NA NA 0 NA NA 0.02
bobyqa 9.889509 5.038000 1.190725e+03 27 NA NA 0 NA NA 0.01
nmkb 9.890341 5.037991 1.190725e+03 69 NA NA 0 NA NA 0.03
hjkb 10.000000 5.000000 1.190775e+03 1 NA 0 9999 NA NA 0.02
ハイパーパラメータ探索
ベイズ最適化をもちいることで、機械学習等のハイパーパラメータ探索も行うことができる。例として、kaggleに登録されているsoar.csv(GormanとSejnowskiがニューラルネットワークを用いたソナー信号の分類の研究で使用したデータセットで が使用したデータセット。ファイルには、金属製の円筒に様々な角度でソナー信号を跳ね返した111のパターンが収録されており、各パターンは0.0から1.0の範囲にあるある周波数帯のエネルギーを一定時間積分した60個の数値の集合。各レコードのラベルには、対象物が岩石であれば “R “の文字が含まれ、地雷(金属製の円筒)は “M “と表示されている)
まずはデータの確認は以下のようにできる。
(def dataset (with-open [data (io/reader "data/sonar.csv")]
(mapv #(-> %
(str/trim)
(str/split #",")
(->> (map read-string))) (line-seq data))))
(count dataset) ;;208
(def xs (map butlast dataset))
(def ys (map (comp keyword last) dataset))
(frequencies ys) ;;111これに対してAda boostでのハイパーパラメータ最適化は以下のようになる。
(defn ada-boost-params
^double [^double trees ^double nodes]
(let [ada-boost (cl/ada-boost {:number-of-trees (int trees)
:max-nodes (int nodes)} xs ys)]
(:accuracy (cl/cv ada-boost))))
(def ada-bounds [[1 (count dataset)]
[2 (count dataset)]])
(ada-boost-params 10 20)
(def ada-boost-bo (o/bayesian-optimization ada-boost-params
{:init-points 5
:kernel (k/kernel :mattern-52 55.0)
:noise 0.05
:utility-param 0.1
:bounds ada-bounds}))
(select-keys (first ada-boost-bo) [:x :y])
(defn draw-2d-2
[bounds bayesian-optimizer iteration]
(let [{:keys [gp xs]} (nth bayesian-optimizer iteration)
cfg {:x (first bounds)
:y (second bounds)
:palette palette
:contours 30}]
(xy-chart {:width 700 :height 300}
(b/series [:contour-2d (fn [x y] (gp [x y])) cfg]
[:contour-2d (fn [x y] (second (gp [x y] true)))
(assoc cfg :position [1 0]
:label "Gaussian processes - std dev")]
[:scatter xs {:size 10
:color (c/darken (first palette))
:margins {:x [0 0] :y [0 0]}
:position [0 0]
:label "Gaussian processes - mean (interpolation)"}])
(b/add-axes :bottom)
(b/add-axes :left))))
(save (draw-2d-2 ada-bounds ada-boost-bo 20) "results/ada-boost.jpg")
次にSVMでのハイパーパラメータ最適化を行う。
(defn svm-params
^double [^double cp ^double cn]
(let [cp (m/pow 10 cp)
cn (m/pow 10 cn)
svm (cl/svm {:c-or-cp cp :cn cn
:kernel (k/kernel :gaussian)} xs ys)]
(m/log (:accuracy (cl/cv svm)))))
(def svm-bounds [[-6 6] [-6 6]])
(m/exp (svm-params 1 1))
(def svm-bo (o/bayesian-optimization svm-params
{:init-points 5
:kernel (k/kernel :mattern-52 1.5)
:utility-param 0.3
:noise 0.05
:bounds svm-bounds}))
(m/exp (:y (nth svm-bo 10)))
(save (draw-2d-2 svm-bounds svm-bo 10) "results/svm.jpg")
Ada-boostと比較してSVMではハイパラパーメータの推定がより収束していることが確認できる。

コメント
[…] Clojureを用いたベイズ最適化ツールの実装 […]
[…] Clojureを用いたベイズ最適化ツールの実装 […]
[…] るため、システマティックなハイパーパラメータ探索を行うことが重要となる。ハイパーパラメータの自動化に関しては”Clojureを用いたベイズ最適化ツールの実装“も参照のこと。 […]