UCB(Upper Confidence Bound)アルゴリズムの概要
“ε-グリーディ法(ε-greedy)の概要とアルゴリズム及び実装例について“で述べているε-greedy法や”ボルツマン分布とソフトマックスアルゴリズム及びバンディット問題“で述べているソフトマックスアルゴリズムでは、腕の探索は確率的に行われ、そのときにアルゴリズムが注目するのは”腕から得られた報酬がいくらか”となる。
そのため、腕から得られる報酬にノイズが含まれ、本当の値にノイズが混じった推定値となってしまうと、初めてデータを処理する際に、簡単にだまされ、否定的な経験をいくつか重ねただけで簡単に誤った判断をしてしまう。ただし、これらのアルゴリズムはランダム性に頼るため、それらの過ちを後のプレイで取り返すことができる。
UCB(Upper Confidence Bound)アルゴリズムは、多腕バンディット問題(Multi-Armed Bandit Problem)において、異なるアクション(または腕)の間で最適な選択を行うためのアルゴリズムであり、アクションの価値の不確実性を考慮し、探索と利用のトレードオフを適切に調整することで、最適なアクションの選択を目指す手法となる。
つまり、腕の推定値に対するユーザーの確信度合いを評価して追跡することで、だまされないようにすることができるアプローチということができる。
これは具体的には確率不等式の一種であるヘフディングの不等式に基づき計算され、イメージ的には以下のようになる。

以下にUCBアルゴリズムの概要について述べる。
まずε-greedy法やSoftmaxアルゴリズムと同様に、アルゴリズムが追跡する情報をすべて格納するクラスを設定する。
class UCB():
def __int__(self, count, values):
self.counts = counts
self.values = values
return
UCBのフィールドパラメータはε-greedy法やSoftmaxアルゴリズムと同様なものになる。異なるのは、countsの活用方法となる。
1. 初期化: 各アクションに対して、初期の推定価値と探索度を設定する。通常、初期の推定価値はゼロまたは他の適切な初期値で初期化され、探索度(または信頼区間の幅)は無限大に設定される。
def initialize(self, n_arms):
self.counts = [0 for col in range(n_arms)]
self.values = [0.0 for col in range(n_arms)]
return2. アクション選択: 各アクションに対して、そのアクションの推定価値に探索度を加えた値を計算する。これは、UCB値と呼ばれ、UCB値が最大のアクションが選択される。
def select_arm(self):
n_arms = len(self.counts)
for arm in range(n_arms):
if self.counts[arm] == 0:
return arm
ucb_values = [0.0 for arm in range(n_arms)]
total_counts = sum(self.counts)
for arm in range(n_arms):
bonus = math.sqrt((2 * math.log(total_counts))/ float(self.counts[arms]))
ucb_values[arm] = self.values[arm] + bonus
return
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n= self.counts[chosen_arm]
value = self.values[chosen_arm]
new_value = ((n-1) / float(n)) * value + (1 / float(n)) * reward
self.valies[chosen_arm] = new_value
return上記のコードはif self.counts[arms]==0で、与えられたすべての腕を一度は引くようにしている。これにより、UCBは確信ベースの決定ルールを適用する前に、全くデータがない状態を避けるようにしている。これは探究する腕の数が多い場合は、初期化に時間がかかるというUCBの特徴を表している。ただし、与えられたすべての選択肢について、少しでも情報を持たせることで、明らかに不利な腕を最初から無視できるという効果もある。
UCBのselect_armメソッドでは、ucb_valueと呼ばれる、それぞれの腕の推定値にボーナス値を加えた値を使う部分に特徴がある。このボーナス値は、ある腕の推定値に、他の腕に比べてその腕について足りない情報いくらか合わせたもので、その値はcounts[arm]がtotal_countsより大きい場合に大きくなり、結果として未知のものを見つけ出そうとする、明示的に好奇心の強いアルゴリズムになるということができる。
UCBがある時点で適切な腕を選択する可能性をプロットしたものを以下に示す。

この動きはε-greedy法やSoftmaxアルゴリズムと比較して、アルゴリズムにランダム性が入っていないにも関わらずノイズが多いものとなる。
3. アクションの実行: 選択されたアクションを実行し、その結果として得られた報酬を観測する。
4. 推定価値の更新: 観測された報酬を用いて、各アクションの推定価値を更新する。通常、報酬の平均値を用いて推定価値を更新し、探索度を減少させる。
5. ステップ2からステップ4を反復的に繰り返す。
UCBアルゴリズムの特徴は、探索度(または信頼区間の幅)を通じて、不確実性を考慮し、未知のアクションを積極的に探索することとなる。初期の段階で各アクションが選択され、より信頼性の高いアクションが特定されるにつれて、探索度が減少し、これにより、最適なアクションに収束することが期待される。
以下にε-greedy法やSoftmaxアルゴリズムとUCBアルゴリズムを比較した結果を示す。

ε-greedy法に比較して、Softmaxアルゴリズムの方が精度はよく、UCBはノイズが見られるがSoftmaxアルゴリズムに近づいていき、試行回数が多くなるとICBアルゴリズムがSoftmaxアルゴリズムを追い越していくことが確認されている。
UCB(Upper Confidence Bound)アルゴリズムの適用事例について
UCB(Upper Confidence Bound)アルゴリズムは多腕バンディット問題(Multi-Armed Bandit Problem)において広く使用されているが、さまざまな適用事例がある。以下にUCBアルゴリズムの主な適用事例を示す。
1. オンライン広告の選択:
UCBアルゴリズムは、オンライン広告の選択に使用されている。異なる広告バリエーションの中から最もクリック率が高い広告を選択し、広告主の収益を最大化するのに役立つ。広告のクリック率は不確かであり、UCBアルゴリズムは探索と利用のトレードオフを調整して最適な広告を選択する。
2. 医療診断と治療計画:
医療分野では、UCBアルゴリズムを使用して最適な診断や治療計画を選択するための研究が行われている。これは患者の病状や反応に関する不確実性を考慮し、治療選択の最適化に貢献する。
3. 再生可能エネルギー管理:
再生可能エネルギー発電の最適制御にUCBアルゴリズムを適用する研究が行われている。風力発電や太陽光発電のようなエネルギー供給が不確実な場合、UCBアルゴリズムは最適な発電制御を達成するのに役立つ。
4. オンライン教育と自動化されたチュータリング:
UCBアルゴリズムは、学習プラットフォームでのオンライン教育や自動化されたチュータリングシステムに適用されている。生徒の能力や理解度に基づいて、最適な問題や課題を選択し、効果的な学習を支援することが可能となる。
5. 無人航空機(ドローン)のパスプランニング:
UCBアルゴリズムは、無人航空機(ドローン)のパスプランニングに使用され、ドローンの飛行経路を最適化し、目標を達成するための最適な経路を決定する。
これらはUCBアルゴリズムの一般的な適用事例の一部です。UCBアルゴリズムは、不確実性を伴う意思決定問題や最適化問題に対して非常に有用であり、実世界のさまざまな領域で利用されており、アクションの選択における不確実性を考慮し、最適な選択を行うための強力なツールとして広く活用されている。
UCB(Upper Confidence Bound)アルゴリズムの実装例について
UCB(Upper Confidence Bound)アルゴリズムの実装は比較的簡単であり、Pythonなどのプログラミング言語を使用して行うことが一般的となる。以下はUCBアルゴリズムの簡単な実装例となる。
import numpy as np
# アクション数
num_actions = 5
# 各アクションの初期化
action_rewards = np.zeros(num_actions) # 各アクションの報酬合計
action_counts = np.zeros(num_actions) # 各アクションの選択回数
# メインのUCBループ
num_rounds = 1000 # ラウンド数
ucb_values = np.zeros(num_actions) # 各アクションのUCB値
for t in range(num_rounds):
# アクション選択
for a in range(num_actions):
if action_counts[a] == 0:
ucb_values[a] = np.inf # 未選択のアクションのUCB値を無限大に設定
else:
ucb_values[a] = action_rewards[a] / action_counts[a] + np.sqrt(2 * np.log(t) / action_counts[a])
selected_action = np.argmax(ucb_values)
# 選択されたアクションを実行して報酬を観測
reward = simulate_reward(selected_action)
# アクションの更新
action_rewards[selected_action] += reward
action_counts[selected_action] += 1
# 最終的な選択確率や報酬を分析
action_selection_probabilities = action_counts / num_rounds
print("各アクションの選択確率:", action_selection_probabilities)
print("各アクションの累積報酬:", action_rewards)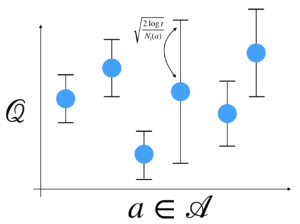





コメント
[…] UCB(Upper Confidence Bound)アルゴリズムの概要と実装例 […]
[…] “UCB(Upper Confidence Bound)アルゴリズムの概要と実装例“でも述べているUpper Confidence Bound (UCB)法は、強化学習やマルチアームバンディット問題などの探索・活用問題において、効率 […]
[…] UCB(Upper Confidence Bound)アルゴリズムの概要と実装例 […]
[…] 初期探索が不足する問題に対処するために、”ε-グリーディ法(ε-greedy)の概要とアルゴリズム及び実装例について“で述べているε-greedy法や”UCB(Upper Confidence Bound)アルゴリズムの概要と実装例“で述べているUCB(Upper Confidence Bound)法と組み合わせることがある。これらのアプローチは、初期段階でより多くの探索を促進し、情報の収集を高めることができる。 […]
[…] 題に応じて他の探索戦略と組み合わせることができも例えば、”UCB(Upper Confidence Bound)アルゴリズムの概要と実装例“で述べているUCB(Upper Confidence Bound)、”Boltzmann Explorationの […]
[…] エクスプロレーション戦略の改良: “ε-グリーディ法(ε-greedy)の概要とアルゴリズム及び実装例について“で述べているε-グリーディ法以外の探索戦略を使用することで、インターミットントリワードの問題に対処できる。例えば、”UCB(Upper Confidence Bound)アルゴリズムの概要と実装例“で述べているUCB(Upper Confidence Bound)や”Thompson Samplingアルゴリズムの概要と実装例“で述べているThompson Samplingなどのバンディットアルゴリズムを組み合わせることがある。 […]