LINE（Large-scale Information Network Embedding）の概要とアルゴリズム及び実装例について

機械学習自然言語処理人工知能デジタルトランスフォーメーションセマンティックウェブ知識情報処理グラフデータアルゴリズム関係データ学習推薦技術異常検知・変化検知技術時系列データ解析 python グラフニューラルネットワーク本ブログのナビ

LINE（Large-scale Information Network Embedding）について

LINE（Large-scale Information Network Embedding）は、グラフデータアルゴリズムの一種で、100万ノード程度の大規模な情報ネットワーク（グラフ）を高速に(通常のPCで数時間で)効率的に埋め込むための手法となる。局所的・大局的なグラフ構造を維持する目的関数を最適化する手法であり、有向・無向グラフや重み付きグラフも対象としている。

LINEはMicrosoft、北京大学、ミシガン大学のメンバーにより”LINE: Large-scale Information Network Embedding“で報告されているもので、ノード（ノードはグラフ内の個々の要素やエンティティを表す）の特徴ベクトル（埋め込み）を学習することを目的としており、これらの特徴ベクトルを使用することで、ノード間の関係や類似性をキャプチャし、さまざまなタスクに応用できるものとなる。

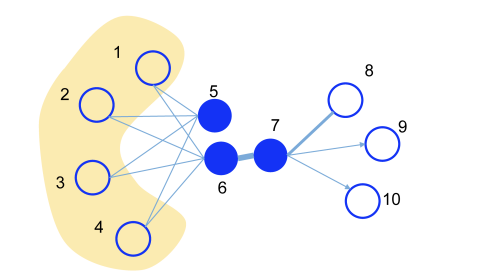
ここでLINEの特徴である1次・2次近接について述べる。

上図において、ノード5とノード6はエッジで結ばれていないが、ノード1からノード4までを介して間接的に繋がっていることから、両ノードの関係性は強いと考えられる。LINEはこのような距離2で繋がった2次近接性も考慮してエンべディングを行っている。

これは例えば多次元尺度法(MDS)、Isomap、Laplacian、Eigenmap(LE、ラプラシアン固有写像)などの従来のグラフエンべディング手法では、隣接行列の主固有ベクトルを求める必要があり、一般にノード数をNとしたときの計算量は\(O(N^3)\)以上となるため、大規模グラフでは計算が困難になる。

これに対して上記の論文では、LINeの特徴として以下のものを挙げている。

LINEは、有向・重み付きグラフにも対応し、数百万ノードまで拡張できる新しいグラフエンべディングとなる。
1次近接性と2次近接性の両方を保持する目的関数を設計し、最適化のためのエッジサンプリングアルゴリズムを開発。従来の確率的勾配降下法の限界を克服し、推論の有効性と効率性を向上した。
実世界の情報ネットワークを対象とした実験を行い、有用であることを実証した。

LINEの主要な特徴は以下のようになる。

1. エッジタイプの学習: LINEは、異なるタイプのエッジ（リンク）間で異なる埋め込みを学習することができる。これにより、異なるタイプのリンクがグラフ内で異なる意味を持つ場合に有用となる。

2. 高次元の埋め込み: LINEは通常、高次元の埋め込み空間でノードを表現する。高次元の埋め込みは、ノード間の微細な類似性をキャプチャしやすくする一方で、計算コストも高くなる。

3. 隣接ノードとの関連性: LINEは、各ノードがその近傍の隣接ノードとどれだけ関連しているかを最適化するように設計されている。この情報は、グラフ内のノードの位置を決定するのに役立つ。

4. 計算効率の向上: LINEは大規模なグラフに対応するために、計算効率を向上させる工夫が施されている。例えば、Negative Sampling（負例サンプリング）を使用して、計算コストを削減する。

LINEは、グラフデータに関連するさまざまなタスクで使用でき、例えば、ノードの類似性の計算、ノード分類、リンク予測、推薦システムなどです。LINEのようなグラフ埋め込みアルゴリズムは、ソーシャルネットワーク分析、バイオインフォマティクス、情報検索、オンライン広告、評判分析、不正検出など、さまざまな応用分野で幅広く利用されている。

LINE（Large-scale Information Network Embedding）に用いられるアルゴリズムについて

LINEにおける問題定義は以下の様になる。グラフ\(\mathbf{G}=(\mathbf{V},\mathbf{E})\)におけるエッジ\(e\in \mathbf{E}\)をノードの順序対e=(u,v)として、それぞれに非負の重み\(\omega_{u,v}\gt 0\)を付与する。一次近接とは、2ノード間の局所的な近接であり、エッジ(u,v)で結ばれたノードuとvの1次近接性は重み\(\omega_{uv}\)となる。1次近接はノードの類似度を表すが、実世界のグラフにおいては観測されるエッジは一部で多くは欠損している。したがって1次近接だけでは不十分であり、友人関係で例えると共通の友人を介した近接性を考える必要がある。

2次近接とは、ノードu,vとエッジで結ばれた隣接ノードの類似度となる。ノードuと他のすべてのノードとの1次近接性を\(p_u=(\omega_{u,1},\omega_{u,2},\dots,\omega_{u,|V|})\)とすると、ノードuとノードvの2次近接性は\(p_u\)と\(p_v\)の類似度となる。もし、uとvの両方とエッジで結ばれたノードがないならば、ノードuとノードvの2次近接性は0になる。

1次近接性のモデルとして、各無向エッジ(i,j)に対して、結合確率を以下の様に定義する。

\[p_1(v_i,v_j)=\frac{1}{1+e^{-\vec{u}_i^T\cdot\vec{u}_j}}\]

ここで、\(\vec{U}_i\in\mathbb{R}^d\)はノード\(v_i\)の低次元のベクトル表現となる。

上式は\(\mathbf{V}\times\mathbf{V}\)空間の分布を定義しており、その経験的確率は\(\hat{p}_1(i,j)=\frac{\omega_{ij}}{\mathbf{W}} \left(ただし\mathbf{W}=\sum_{(i,j)\in E}\omega_{ij}\right)\)で定義できる。1次近接性を維持するための率直な方法は以下の目的関数を最小化することにある。

\[O_1=d(\hat{p}_1(\cdot , \cdot),\ p_1(\cdot , \cdot))\]

ここでd(・, ・)は2つの分布間の距離となる。このdをKL-divergenceに置き換え、定数を除去すると以下の式が得られる。

\[O_1=-\displaystyle\sum_{(i,j)\in E}\omega_{ij}log p_1(v_i,v_j)\]

この式を最小化する\(\{\vec{u}_i\}_{i=1\dots |V|}\)を求めることで、各ノードをd次元で表せることとなる。

2次近接性は、他の多くのノードとの結合を共有するノードは互いに似ているとの仮定の下に定義されている。各ノードは、ノードそのものと、他のノードのコンテキストとしての2つの役割を持つ。ノード\(v_i\)に対して、\(\vec{u}_i\)と\(\vec{u}_i’\)の2つのベクトルを導入する。前者はノード\(v_i\)そのものの表現であり、後者はコンテキストとしての表現である。各有向エッジ(i, j) について、ノード\(v_i\)によって作られた\(v_j\)のコンテキストの確率を以下のように定義する。

\[p_2(v_j|v_i)=\frac{e^{\vec{u’}^T\cdot\vec{u}_i}}{\sum_{k=1}^{|V|}e^{\vec{u’}_k^T\cdot \vec{u}_i}}\]

ここではノード|V|(コンテキスト)数となる。

各ノードについて、上式はコンテキスト(ネットワークの全ノード集合)に対する条件付き確率分布\(p_2(\cdot |v_i)\)を定義している。 2次近接性を保つためには、低次元表現であるコンテキストの条件付き確率分布\(p_2(\cdot |v_i)\)を、経験的確率\(\hat{p}_2(\cdot | v_i)\)に近づける必要がある。したがって、以下の目的関数を最小化するものとなる。

\[O_2=\displaystyle\sum_{i\in V}\lambda_i d(\hat{p}_2(\cdot |v_i),\ p_2(\cdot |v_i))\]

ここでは2つの分布の距離となる。一般にグラフのノードの重要度は異なるので、目的関数の中に\(\lambda_i\)を導入してノードiのグラフにおける重要度を表す。具体的には次数やページランク (PageRank)などによって表す。経験的確率\(\hat{p}_2(\cdot | v_i)\)は、\(\hat{p}_2(v_j | v_i)=\frac{\omega_{ij}}{d_i}\)によって定義される。ここではエッジ(i, j)の重みであり、\(d_i\)はノードi の出次数(\(d_i=\sum_{k\in N(i)}\omega_{ik}\)、N(i)はノードi から他のノードへのエッジによる近傍の集合)となる。 LINEでは単純化のために、\(\lambda_i=d_i\)としている。また、分布間の距離関数にはKL-divergenceを用いている。前述の式においてd(・|・)をKL-divergenceに置き換え、 \(\lambda_i=d_i\)として定数を除去すると、以下の式を得る。

\[O_2=-\displaystyle\sum_{(i,j)\in E}\omega_{ij}log p_2(v_j|v_i)\]

この目的関数を最小化する \(\{\vec{u}_i\}_{i=1,\dots,|V|}\)と\(\{\vec{u}_i’\}_{i=1,\dots,|V|}\)を学習することで、各ノード\(v_i\)をd次元ベクトル\(\vec{u}_i\)で表すことができる。 1次近接性と2次近接性を保持するエンベディングを実現するための単純で効果的な方法として、1次近接性を保持するものと、 2次近接性を保持するものとを別々に訓練して、それぞれで得られた各頂点のエンベディングを結合している。両方の目的関数を同時に最適化するやり方については今後の課題とされている。上式の最適化は、条件付き確率\(p_2(\cdot |v_i)\)を計算する際にすべてのノード集合についての和を計算する必要があるため、計算量が大きい。この問題を解決するため、各エッジ(i, j)の雑音分布に従ったnegative samplingを行う。 LINEの計算量は、エッジ数|E| に比例し、ノード数|V| にはよらないため、大規模ネットワークにおいて他手法に比べて高速に実行できる。

LINEはノードの類似性や関連性を包括的に捉えることができ、大規模な情報ネットワークに対して効果的な埋め込みを生成するアルゴリズムとなっており、この埋め込みは、さまざまなグラフデータ関連のタスクに応用できる。

“LINE: Large-scale Information Network Embedding“では、実験として言語ネットワーク(Wikipedia)、社会ネットワーク(FlickerとYouTube)、引用ネットワーク(BDLP)を用いて、Graph Fractorization、”DeepWalkの概要とアルゴリズム及び実装例について“で述べられているDeepWalk、”Skipgramの概要とアルゴリズム及び実装例“でも述べているSkipGramと比較して言語類推や文書分類のタスクにおいて優位であると報告されている。

筆者によるgitページにてコードが公開されている。

LINE（Large-scale Information Network Embedding）の実装例について

LINE（Large-scale Information Network Embedding）は、グラフデータを埋め込むアルゴリズムだが、その実装はプログラム言語やライブラリに依存している。以下は、Pythonと一般的な機械学習ライブラリを使用したLINEの実装例となる。

import numpy as np
import networkx as nx
from gensim.models import Word2Vec

# グラフの読み込み
G = nx.read_edgelist("graph.txt", create_using=nx.Graph())

# LINEの実装
def LINE(graph, dimensions, walk_length, num_walks):
    walks = []
    for _ in range(num_walks):
        for node in graph.nodes():
            walk = random_walk(graph, node, walk_length)
            walks.append(walk)
    
    model = Word2Vec(walks, vector_size=dimensions, sg=1, hs=1)
    
    return model

def random_walk(graph, start_node, walk_length):
    walk = [start_node]
    while len(walk) < walk_length:
        neighbors = list(graph.neighbors(walk[-1]))
        if len(neighbors) == 0:
            break
        next_node = np.random.choice(neighbors)
        walk.append(next_node)
    return [str(node) for node in walk]

# LINEの呼び出し
dimensions = 128
walk_length = 10
num_walks = 100
line_model = LINE(G, dimensions, walk_length, num_walks)

# 埋め込みベクトルの取得
node_embeddings = {node: line_model.wv[str(node)] for node in G.nodes()}

この実装例では、以下のステップを実行している。

グラフデータを読み込む。ここでは、networkxライブラリを使用しているが、データの形式に応じて適切な方法でグラフを読み込む必要がある。
LINEアルゴリズムを実装する。ランダムウォークを実行し、それをWord2Vecモデルに供給してノードの埋め込みを学習する。LINEアルゴリズムは、グラフのランダムウォークを行い、それをWord2Vecとして学習することによって、ノードの埋め込みベクトルを生成する。
埋め込みベクトルを取得する。LINEモデルを使用して、各ノードの埋め込みベクトルを抽出する。

LINE（Large-scale Information Network Embedding）の課題について

LINE（Large-scale Information Network Embedding）は、優れたグラフ埋め込みアルゴリズムだが、いくつかの課題や制約も存在する。以下にそれら課題について述べる。

1. 計算コスト: LINEは高次元の埋め込み空間での学習を行うため、大規模なグラフに対しては計算コストが高くなることがある。特に、2nd-order Proximity（2nd-Order Similarity）を考慮する場合、共通の隣接ノードの数が多いと計算が爆発的に増加する。

2. ハイパーパラメータの調整: LINEにはいくつかのハイパーパラメータ（埋め込み次元、ウォークの長さ、ウォークの回数など）が存在し、これらのパラメータの調整が必要となる。適切なハイパーパラメータの選択はタスクに依存し、手動で調整する必要があることがある。

3. 非同次グラフへの対応: LINEは同次グラフ（単一のノードタイプと単一のエッジタイプを持つグラフ）に適しており、非同次グラフ（複数のノードタイプやエッジタイプを持つグラフ）への適用が難しいことがある。非同次グラフでは、異なるノードタイプやエッジタイプに対する関連性を考慮する必要がある。

4. ストリームデータへの適用: LINEは静的なグラフに対して設計されており、動的なストリームデータに対する適用が難しいことがある。グラフが時間経過に伴って変化する場合、LINEの埋め込みは追従できない可能性がある。

5. スケーラビリティ: LINEは大規模なグラフに対しても効率的に埋め込みを学習できるように設計されているが、それでも一部の非常に大きなグラフには適用が難しいことがある。より高速でスケーラブルなアルゴリズムが求められる。

LINE（Large-scale Information Network Embedding）の課題への対応策について

LINE（Large-scale Information Network Embedding）の課題に対処するために、いくつかの対策が考えられる。以下に、LINEの主な課題に対する対応策について述べる。

1. 計算コストへの対処:

ミニバッチ学習: ランダムウォークを行う際に、すべてのウォークを一度に処理せず、”ミニバッチ学習の概要とアルゴリズム及び実装例“でも述べているミニバッチ学習を導入することで計算コストを削減できる。この方法により、大規模なグラフでも学習を効率的に行うことが可能となる。

2. ハイパーパラメータの調整への対処:

自動チューニング: ハイパーパラメータの最適な設定を見つけるために、ハイパーパラメータの自動チューニングツールを使用することができる。例えば、ベイズ最適化やグリッドサーチを活用して、最適なパラメータを見つけるようにものとなる。

3. 非同次グラフへの対応への対処:

モデルの拡張: 非同次グラフに対処するために、LINEのモデルを拡張することができる。これにより、異なるノードタイプやエッジタイプに関する情報を組み込むことができ、例えば、”Metapath2Vecの概要とアルゴリズム及び実装例“で述べているMetapath2Vecなどの手法を考慮することができる。

4. ストリームデータへの対処への対処:

動的なグラフ埋め込み: グラフが時間経過に伴って変化する場合、動的なグラフ埋め込みアルゴリズムを検討することができる。例えば、DynamicLINEや”GraphSAGEの概要とアルゴリズム及び実装例について“で述べているGraphSAGEのようなアルゴリズムは、ストリームデータに適している。

5. スケーラビリティへの対処:

分散処理: 大規模なグラフに対処するために、分散処理フレームワークを使用することができる。例えば、Apache Sparkやグラフデータベースを活用することで、処理能力を向上させる。

6. グラフサンプリング:

大規模なグラフをサブグラフにサンプリングして処理することで、計算コストを低減する方法もある。ランダムウォークにおいては、サブグラフのランダムウォークを実行することが考えられる。

7. 最新のアルゴリズムの利用:

LINEの改良版や他のグラフ埋め込みアルゴリズムを検討することも重要となる。グラフデータ解析の分野では新たなアルゴリズムが頻繁に提案されており、課題に応じて最適なアルゴリズムを選択することが有益となる。