グラフデータ処理アルゴリズムと機械学習/人工知能タスクへの応用

機械学習技術 関係データ学習 Clojure デジタルトランスフォーメーション技術 人工知能技術 自然言語処理技術 セマンティックウェブ技術 オントロジー技術 検索技術 アルゴリズム 確率的生成モデル サポートベクトルマシン スパースモデリング C/C++言語と各種機械学習アルゴリズム 本ブログのナビ

グラフデータ処理アルゴリズムについて

グラフはものや状態といった対象同士の結びつきを表すための表現方法となる。多くの問題をグラフの問題に帰着することができるため、グラフに関するアルゴリズムが多く提案されている。

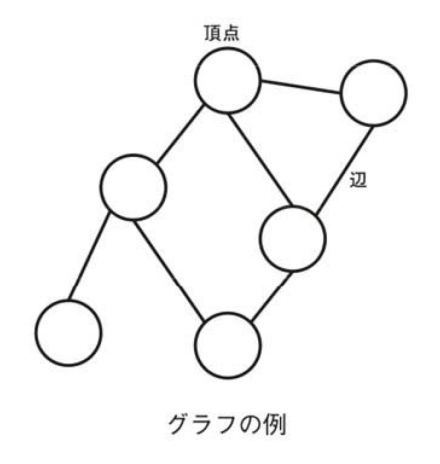
グラフは頂点(vertex,node)と辺(edge)からなる。頂点は対象を表し、図では点や円で絵かがれる。辺は2つの対象の結びつきを表し、図では2点を結ぶ線分として描かれる。頂点の集合がV、辺の集合がEであるようなグラフをG=(V,E)と表し、2点u,vを結ぶ辺をe=(u,v)と表す。

グラフには大きく分けて2つの種類がある。辺に向きがないグラフを無向グラフ、辺に向きがあるグラフを有向グラフという。友人関係のグラフ(人を頂点として友人関係を辺とするグラフ)や路線図は無向グラフであり、数の大小関係のグラフ(数を頂点としてA>BのときAからBに辺を引いたグラフ)やフローチャートは有向グラフとなる。

辺にはさまざまな属性がつくことがある。代表的なものに重み(cost)がある。辺に重みのついたグラフを重み付きグラフと言う。重みは問題によって、距離や時間や価格などさまざまに解釈される。

2つの頂点の間に辺があるとき、その2つの頂点を隣接していると言う。隣接している頂点の列をパスという。始点と終点が同じようなパスを閉路という。任意のニ頂点間にパスが存在するようなグラフを連結グラフという。頂点につながっている辺の数を、その頂点の次数という。

連結グラフで、閉路を持ちないものを木(tree)と言い、連結でないグラフで閉路を持たないものを森と言う。木は辺の数がちょうど頂点-1になっている。辺の数が頂点-1に等しい連結なグラフは木になる。

根(root)と呼ばれる頂点を一つ選ぶと、根を一番上で、根から遠い頂点ほど下になるように木を配置することができる。このような木を棍付き木と呼ぶ。棍付き木でない普通の木も、適当に頂点を選んで棍付き木にすることで扱いやすくなる場合がある。棍付き木を家系図のように見立てると、頂点の間に親子関係を与えることができる。これは、辺に向きを与えたと考えることもできる。

ここでは、有向グラフの頂点vに対して、vから出ていく辺の集合をδ+(v)、入ってくる辺の集合をδ-(v)と表記する。|δ+(v)|をvの出次数、|δ-(v)|を入次数と呼ぶ。

有向グラフで閉路を持たないグラフをDAG(Directed Acyclic Graph)と呼ぶ。たとえば整数を頂点とし、nがmを割り切るときにnからmに辺を引いてグラフを考えると、これはDAGになる。この場合のようにDAGの頂点の間には順序関係を与えることができる。

拡張点に対して番号をつけ、i番目の頂点をviとする。頂点viから頂点vjに向かって辺があるとき、i<jが成り立つような番号の付け方をトポロジカル順序と呼ぶ。

トポロジカル順序に従って頂点を左から右に並び替えると、すべての辺は左から右に向かうようになる。このような順序をつけることで、DAGの問題をDPを用いて解けるようになることもある。トポロジカル順序を求めることをトポロジカルソートと呼ぶ。

グラフをプログラムで扱うためには、頂点や辺を具体的なデータとして持つ必要がある。グラフの表現方法として代表的なものに、隣接行列と隣接リストがある。どちらの表現にも利点と欠点があり、問題によっては計算量に影響を与えるものがある。以下V、Eを頂点と辺の集合、|V|、|E|を頂点と辺の個数とする。またVに0〜|V|-1の番号がふられているとする。

まず隣接行列について。隣接行列では|V|x|V|の二次元配列gでグラフを表現する。g[i][j]はi番目の頂点とj番目の頂点の間の関係を示すものとなる。

無向グラフの場合は「i番目の頂点とj番目の頂点が辺で結ばれているか」の情報があればよいので、g[i][j]とg[j][i]の値を頂点iと頂点jが辺で結ばれているなら1、そうでないなら0とすることで無向グラフを表現することができる。

有向グラフの場合は「頂点iから頂点jへ向かう辺があるか」の情報があればいいので、g[i][j]の値を頂点iから頂点jへ向かう辺があるなら1、そうでないなら0とすることで有向グラフを表現することができる。この場合は無向グラフと異なりg[i][j]≠g[j][i]となる。

重み付きグラフの場合はg[i][j]を頂点iから頂点jへの辺の重みとする。辺がないときは0ら入れると重みが0の場合と区別がつかなくなるので、適当に大きな(区別できればなんでも良い)定数INFを定義しておいてg[i][j]=INFとしておく。当然無向グラフならg[i][j]=g[j][i]となる。いくつも属性がある場合は、同じように|V|x|V|の配列を複数個用意するか、配列の要素を構造体やクラスにすれば同じように扱える。

隣接行列の利点は、ニ頂点間に辺があるかが定数時間で判定できることなどがあるが、常にO(|V|²)のメモリを確実に消費している。辺が少ない場合は無駄な領域が大量にできる。例えば木を考えてみると、辺の数はちょうど|V|-1なので、配列gのほとんどの要素は0で埋まっていることになる。|V|が1000000の場合だと、gの要素が1バイトでもメモリは1TB近く証拠している。

また多重辺や事故ループがある場合には注意が必要となる。

重み付きでない場合はg[i][j]に頂点iから頂点jへの辺の個数を入れれば良いが、重み付きの場合は複雑となる。大抵の場合は、重みが最小(最大)のものがあればよいので、それ以外は無視するというてもあるが、どうしても多重辺を保持したい場合は、次に述べる隣接リストを使う。

隣接行列の場合、変の数が少ないと無駄にメモリを消費するが、隣接リストの場合は「頂点0から頂点2,4,5に辺がある」といった情報をリストとして持つことでグラフを表現する。この場合はO(|V|+|E|)しかメモリを消費しない。

実際に隣接リストを実装する方法にはさまざまなものがある。重み付きグラフなど辺に属性がある場合、辺を表す構造体やクラスを作ってしまうと管理がしやすく、メモリの消費も少なくなる。

これらのグラフ構造を使うことで探索問題、2部グラフ判定(色分け)、最短距離、最小全域木等の問題を解くことができる。また、機械学習技術と組み合わせたアルゴリズムも用いられている。それらを以下に示す。

機械学習での実装

• SNAP (Stanford Network Analysis Platform)の概要と実装例について

SNAPは、Stanford大学のコンピュータサイエンス研究室で開発されたオープンソースのソフトウェアライブラリであり、ソーシャルネットワーク分析、グラフ理論、コンピュータネットワーク分析など、さまざまなネットワーク関連の研究に使用されるツールとリソースを提供しているものとなる。

• CDLib (Community Discovery Library)の概要と適用事例及び実装例について

CDLib（Community Discovery Library）は、コミュニティ検出アルゴリズムを提供するPythonライブラリであり、グラフデータにおけるコミュニティ構造を特定するためのさまざまなアルゴリズムを提供し、研究者やデータサイエンティストが異なるコミュニティ検出タスクに対処できるようサポートするものとなる。

• MODULAR (Multi-objective Optimization of Dynamics Using Link and Relaxations)の概要と適用事例及び実装例について

MODULARは、複雑なネットワークの多目的最適化問題を解決するための計算機科学およびネットワーク科学の研究領域で使用される手法やツールの1つであり、このアプローチは、ネットワークの構造とダイナミクスを同時に最適化するために設計されており、異なる目的関数（多目的最適化）を考慮に入れたものとなっている。

• Louvain法の概要と適用事例及び実装例について

Louvain法（またはLouvainアルゴリズム）は、ネットワーク内のコミュニティ（クラスター）を特定するための効果的なグラフクラスタリングアルゴリズムの一つであり、このアルゴリズムは、ネットワークのノードとエッジを基に、ノードをコミュニティに分割するものとなる。Louvain法は、コミュニティの構造を特定するためにモジュラリティと呼ばれる尺度を最大化するアプローチを採用している。

• Infomapの概要と適用事例及び実装例について

Infomap（Information-Theoretic Modularity）は、コミュニティ検出アルゴリズムの一つで、ネットワーク内のコミュニティ（モジュール）を特定するために使用されるものとなる。Infomapは情報理論に基づいており、ネットワーク内の情報のフローと構造を最適化することに焦点を当てている。

• Copraの概要と適用事例及び実装例について

Copra（Community Detection using Partial Memberships）は、コミュニティ検出のためのアルゴリズムおよびツールの1つであり、複雑なネットワーク内でのコミュニティの検出と特定のノードが複数のコミュニティに属することを考慮に入れたアルゴリズムとなる。Copraは、部分的なコミュニティメンバーシップ情報を使用して、各ノードが複数のコミュニティに所属することができるという現実的なシナリオに適している。

• IsoRankNの概要とアルゴリズム及び実装例について

IsoRankNは、ネットワークアラインメント（Network Alignment）のためのアルゴリズムの一つで、ネットワークアラインメントは、異なるネットワーク間の対応する頂点のマッピングを見つける問題であり、IsoRankNはこの課題に対する効果的な解法の一つとなる。IsoRankNは、IsoRankアルゴリズムの改良版であり、異なるネットワーク間での頂点の対応付けを高精度かつ効率的に行う。IsoRankNは、異なるネットワークの構造や特性を考慮して頂点をマッピングし、異なるネットワークにおける相似性を保持することを目指している。

• 時間と共に変化していくグラフデータを解析する手法について

時間と共に変化するグラフデータを解析する手法は、ソーシャルネットワーク分析、ウェブトラフィック分析、バイオインフォマティクス、金融ネットワークモデリング、交通システム解析など、さまざまなアプリケーションに適用されている。ここではこの技術の概要とアルゴリズム及び実装例について述べている。

• スナップショット解析による時間的な変化を考慮に入れるグラフデータ解析

スナップショット解析（Snapshot Analysis）は、データの異なる時間点でのスナップショット（瞬間のデータスナップショット）を使用して、時間的な変化を考慮に入れたデータ解析の手法となる。この手法は、時間に関する情報を持つデータセットを分析し、そのデータの時間的なパターン、トレンド、および変化を理解するのに役立ち、グラフデータ解析と組み合わせることで、ネットワークや関係性データの時間的な変化をより深く理解することができるようになる。ここでは、このアプローチの概要とアルゴリズム及び実装例について述べている。

• ダイナミックコミュニティ分析について

ダイナミックコミュニティ分析（Dynamic Community Detection）は、時間に関連する情報を持つネットワーク（ダイナミックネットワーク）内で、コミュニティ（モジュールまたはクラスタ）の時間的な変化を追跡および解析するための手法となる。通常、ノードとエッジが時間に関連した情報を持つグラフデータ（ダイナミックグラフ）を対象としており、この手法は、さまざまな分野で応用され、例えばソーシャルネットワーク分析、バイオインフォマティクス、インターネットトラフィックモニタリング、金融ネットワーク分析などで利用されている。

• ダイナミック中心性指標による時間的な変化を考慮に入れるグラフデータ解析

ダイナミック中心性指標（Dynamic Centrality Metrics）は、時間的な変化を考慮に入れたグラフデータ解析の一種であり、通常の中心性指標（例: 次数中心性、媒介中心性、固有ベクトル中心性など）は、静的なネットワークに適しており、ネットワーク内のノードの重要性を単一のスナップショットで評価するものとなる。しかし、実際のネットワークは時間に関連する要素を持つことが多いため、ネットワークの時間的な変化を考慮することが重要となる。

• ダイナミックモジュール検出による時間的な変化を考慮に入れるグラフデータ解析

ダイナミックモジュール検出は、時間的な変化を考慮に入れたグラフデータ解析の手法の一つであり、この手法は、ダイナミックネットワーク内でコミュニティ（モジュール）の変化を追跡し、異なる時間スナップショットでのコミュニティ構造を特定するものとなる。ここではダイナミックモジュール検出に関する詳細とその実装例についての情報を示す。

• ネットワークアライメントによる時間的な変化を考慮に入れるグラフデータ解析

ネットワークアライメントは、異なるネットワークやグラフ間で類似性を見つけ、それらをマッピングし合わせる技術であり、時間的な変化を考慮に入れるグラフデータ解析にネットワークアライメントを適用することで、異なる時間スナップショットのグラフを対応付け、その変化を理解することが可能とするものとなる。

• 時間予測モデルを用いた時間的な変化を考慮に入れるグラフデータ解析

時間予測モデルを用いた時間的な変化を考慮に入れるグラフデータ解析は、グラフデータ内の時間的なパターン、トレンド、予測を理解するために使用される。ここではこのアプローチについての詳細について述べる。

• テンソル分解法によるダイナミックモジュール検出について

テンソル分解法（Tensor Decomposition）は、高次元のテンソルデータを低ランクのテンソルに近似する手法であり、この手法は、データの次元削減や特徴抽出に使用され、機械学習やデータ解析のさまざまなアプリケーションで有用なアプローチとなる。ダイナミックモジュール検出にテンソル分解法を適用することは、時系列データや動的なデータモジュールの検出といったタスクに関連する。

• MAGNA (Maximizing Accuracy in Global Network Alignment)の概要とアルゴリズム及び実装例について

MAGNAは、生物学的ネットワークにおいて、異なる種類のノード（たとえば、タンパク質や遺伝子）を対応付けるためのアルゴリズムやツールのセットであり、生物学的ネットワークマッチングは、異なるデータソースからの情報を統合し、異なる種類の生物学的実体間の関係を特定するのに役立つアプローチとなる。

• TIME-SI (Time-aware Structural Identity)の概要とアルゴリズム及び実装について

TIME-SI（Time-aware Structural Identity）は、時間に関連する情報を考慮に入れてネットワーク内のノード間の構造的な対応を特定するためのアルゴリズムまたは手法の一つであり、TIME-SIは、生物学的ネットワークやソーシャルネットワークなど、さまざまなネットワークデータで使用されているものとなる。

• グラフデータのDiffusion Modelsの概要とアルゴリズム及び実装例について

グラフデータのDiffusion Modelsは、ネットワーク上で情報や影響がどのように広がるかをモデル化する手法であり、ソーシャルネットワークやネットワーク構造を持つデータでの影響の伝播や情報の拡散を理解し、予測するために使用されるものとなる。以下にグラフデータのDiffusion Modelsの基本的な概要について述べる。

• GRAALの概要とアルゴリズム及び実装例について

GRAAL（Graph Algorithm for Alignment of Networks）は、生物学的ネットワークやソーシャルネットワークなど、異なるネットワークデータ間で対応付け（アライメント）を行うためのアルゴリズムであり、主に生物学的ネットワークの比較や解析に使用されるものとなる。GRAALは、ネットワーク対応付けの問題を解決し、異なるネットワーク間の共通の要素（ノードやエッジ）を特定するために設計されている。

• HubAlignの概要とアルゴリズム及び実装例について

HubAlign（Hub-based Network Alignment）は、異なるネットワーク間での対応付け（アライメント）を行うためのアルゴリズムであり、異なるネットワーク間で共通の要素（ノードやエッジ）を特定するために使用されるものとなる。これは主にバイオインフォマティクスやソーシャルネットワーク分析などの領域で活用されている。

• IsoRankの概要とアルゴリズム及び実装例について

IsoRank（Isomorphism Ranking）は、異なるネットワーク間での対応付け（アライメント）を行うためのアルゴリズムの一つであり、ネットワーク同型性（グラフ同型性）を利用して、2つの異なるネットワーク間で類似性を計算し、それに基づいてノードの対応を推定するものとなる。IsoRankは、異なるネットワーク間でのデータ統合、ネットワーク比較、バイオインフォマティクス、ソーシャルネットワーク解析などの分野で利用されている。

• ワイアット・ミラー・ターマンアルゴリズム (Weisfeiler-Lehman Algorithm)の概要と関連アルゴリズム及び実装例について

ワイアット・ミラー・ターマンアルゴリズム（Weisfeiler-Lehman Algorithm、W-Lアルゴリズム）は、グラフ同型性テストのためのアルゴリズムであり、主に、与えられた2つのグラフが同型かどうかを判断するために使用されるものとなる。

• DynamicTriadの概要とアルゴリズム及び実装例について

DynamicTriadは、動的なグラフデータの時間的な変化をモデル化し、ノードの対応関係を予測するための手法であり、このアプローチは、動的なネットワークでの対応関係の予測やノードの時間的な変化の理解に応用されている。

• MODA (MOdule Detection in Dynamic Networks Algorithm)の概要と実装例について

MODAは、動的ネットワークデータにおいて、モジュール（ノードのグループ）を検出するためのアルゴリズムであり、MODAは、時間的な変化を考慮に入れ、ネットワーク内のモジュールがどのように進化するかを追跡することができるように設計されたものとなる。このアルゴリズムは、動的ネットワークの解析、コミュニティ検出、エボリューションの研究など、さまざまな応用に役立っている。

• DynamicTriadの概要とアルゴリズム及び実装例

DynamicTriad（ダイナミックトライアド）は、人々や組織、その他の要素間の関係を調査し、そのネットワーク構造や特性を理解するための手法である社会ネットワーク分析（SNA）の分野で使われるモデルの一つとなる。DynamicTriadは、”Clojureを用いたネットワーク解析(2)Glitteringを使ったグラフ中の三角の計算“でも述べている様に3つの要素で構成されるトライアド（三つ組の集合）の変化を追跡し、ネットワーク全体の進化を理解するためのツールとなる。これは、ネットワーク内の個々の関係だけでなく、グループやサブグループの動きも考慮に入れることができるため、より包括的なネットワークの分析が可能なアプローチとなる。

• Girvan-Newmanアルゴリズムの概要と実装例について

Girvan-Newmanアルゴリズムは、グラフ理論においてネットワークのコミュニティ構造を検出するためのアルゴリズムであり、このアルゴリズムは、エッジの媒介中心性（betweenness centrality）を利用して、ネットワーク内の重要なエッジを特定し、それらのエッジを取り除くことでネットワークをコミュニティに分割するものとなる。

• 大規模グラフデータのサブサンプリングについて

大規模グラフデータのサブサンプリングは、グラフの一部をランダムに選択することで、データのサイズを削減し、計算およびメモリの使用量を制御するもので、大規模なグラフデータセットを扱う際に、計算効率を向上させるためのテクニックの一つとなる。ここでは、大規模グラフデータのサブサンプリングに関するいくつかのポイントとテクニックについて述べる。

• タイムライン上でグラフスナップショットを表示したり、アニメーション化する手法

タイムライン上でグラフスナップショットを表示したり、アニメーション化することは、時間的な変化を視覚化し、グラフデータの動的な特性を理解するのに役立ち、グラフデータを解析する上で重要な手法となる。ここではこれらに用いられるライブラリ及び実装例について述べている。

• NetworkXとmatplotlibを組み合わせたグラフのアニメーションの作成について

Pythonでネットワークの動的な変化を視覚的に表現するための手法であるNetworkXとMatplotlibを組み合わせたグラフのアニメーションの作成について述べる。

• 高次元のデータを次元削減技術（例: t-SNE、UMAP）を使用して低次元にプロットし、可視化を容易にする手法について

高次元のデータを次元削減技術を使用して低次元にプロットし、可視化を容易にする手法は、データの理解、クラスタリング、異常検出、特徴量選択など多くのデータ分析タスクで有用となる。ここでは主要な次元削減技術とその手法について述べる。

• Gephiを用いたデータの可視化について

Gephiは、オープンソースのグラフ可視化ソフトウェアで、ネットワーク分析や複雑なデータセットの可視化に特に適したツールとなる。ここではGephiを使用してデータを可視化する基本的なステップと機能について述べる。

• Cytoscape.jsを用いたデータの可視化について

Cytoscape.jsは、JavaScriptで書かれたグラフ理論ライブラリであり、ネットワークやグラフデータの可視化を行うために広く使用されているものとなる。Cytoscape.jsを使用することで、ウェブアプリケーションやデスクトップアプリケーションに対してグラフやネットワークデータの可視化を追加することが可能となる。ここではCytoscape.jsを用いたデータの可視化に関する基本的なステップとコードの例を示す。

• Sigma.jsを用いたグラフデータの可視化について

Sigma.jsは、Webベースのグラフ可視化ライブラリで、対話的なネットワーク図を作成するのに役立つツールとなる。ここではSigma.jsを使用してグラフデータを可視化するための基本的な手順と機能について述べる。

• ベイジアンニューラルネットワークの概要とアルゴリズム及び実装例について

ベイジアンニューラルネットワーク（BNN）は、確率論的な要素をニューラルネットワークに統合するアーキテクチャであり、通常のニューラルネットワークが確定論的であるのに対し、BNNはベイズ統計に基づいて確率的なモデルを構築するものとなる。これにより、モデルが不確実性を考慮できるようになり、さまざまな機械学習タスクで応用されている。

• ページランクアルゴリズムの概要と実装

ページランクアルゴリズムは、Googleの共同創業者であるラリー・ページ（Larry Page）によって考案されたアルゴリズムで、ウェブページの重要度を計算するために使用されるアルゴリズムとなる。グーグルを現在の位置に押し上げたのは、このページランクアルゴリズムを用いた検索技術の革新によるものとなる。ページランク技術は、検索エンジンの要素技術のうちの検索結果のランク付け技術にあたる。ここではこのページランクアルゴリズムの概要と実装例について述べている。

• 機械学習における類似度について

類似性（similarity）は、二つ以上のオブジェクトや事物が共通の特徴や性質を持ち、互いに似ていると見なされる程度を表す概念であり、比較や関連性の観点からオブジェクトを評価したり、分類やグループ化を行ったりする際に重要な役割を果たしている。ここでは、様々なケースでの類似度の概念と一般的な計算方法について述べている。

• 有向非巡回グラフの適用事例と実装例およびブロックチェーン技術について

有向非巡回グラフ(Directed Acyclic Graph, DAG)は、様々なタスクの自動管理、あるいはコンパイラ等の処理など様々な場面で登場するグラフデータアルゴリズムとなる。今回は、このDAGについて述べてみたいと思う。

• 関係データ学習の概要と適用事例および実装例

関係データ学習(Relational Data Learning)は、関係データ(例：グラフ、ネットワーク、表形式のデータなど)を対象とした機械学習の手法となる。従来の機械学習は通常、個々のインスタンス(例：ベクトルや行列)に対してのみ適用されていたが、関係データ学習は複数のインスタンスとその間の関係性を考慮するものとなる。

ここではこの関係データ学習に対して、様々な適用事例と、スペクトラルクラスタリング、行列分解、テンソル分解、確率的ブロックモデル、グラフニューラルネットワーク、グラフ畳み込みネットワーク、グラフ埋め込み、メタパスウォーク等のアルゴリズムでの具体的な実装について述べている。

• ナレッジグラフの自動生成と様々な実装例

ナレッジグラフは、情報を関連性のあるノード(頂点)とエッジ(つながり)の集合として表現するグラフ構造であり、異なる主題やドメインの情報を結び付け、その関連性を可視化するために使用されるデータ構造となる。ここではこのナレッジグラフの自動生成に関して様々な手法での概要とpythonによる具体的な実装について述べている。

• ナレッジグラフの様々な活用と実装例

ナレッジグラフは、情報を関連性のあるノード(頂点)とエッジ(つながり)の集合として表現するグラフ構造であり、異なる主題やドメインの情報を結び付け、その関連性を可視化するために使用されるデータ構造となる。ここではこのナレッジグラフの様々な活用事例とpythonによる具体的な実装例について述べる。

• 構造学習の概要と各種適用事例および実装例

構造学習(Structural Learning)は、機械学習の一分野であり、データの構造や関係性を学習する手法を指し、通常、教師なし学習や半教師あり学習の枠組みで使用されるものとなる。構造学習は、データの中に存在するパターン、関係性、または構造を特定し、それをモデル化し、データの背後にある隠れた構造を明らかにすることを目的としている。構造学習は、グラフ構造、木構造、ネットワーク構造など、さまざまなタイプのデータ構造を対象としている。

ここでは、この構造学習に関して様々な適用事例と具体的な実装例について述べている。

• Clojureを用いたネットワーク解析(2)Glitteringを使ったグラフ中の三角の計算

GraphXは、Sparkと連携して動作するように設計された分散グラフ処理ライブラリとなる。 “Apache SparkとMLlibによる大規模な機械学習“で述べたしたMLlibライブラリのように、GraphXはSparkのRDDの上に構築された一連の抽象化機能を提供する。グラフの頂点と辺をRDDとして表現することで、GraphXは非常に大きなグラフをスケーラブルに処理することができる。

グラフ並列システムは、表現できる計算の種類を制限し、グラフを分割・分散する技術を導入することで、高度なグラフアルゴリズムを一般的なデータ並列システムより数桁速く効率的に実行することが可能となる。

• Clojureを用いたGraphX Pregelでのネットワーク解析

Pregel APIは、カスタムで反復的なグラフ並列計算を表現するための、GraphXの主要な抽象化機能となる。この名前は、Googleが2010年に発表した大規模グラフ処理を実行するための社内システムにちなんで付けられた。また、”Clojureを用いたネットワーク解析(1) 幅優先/深さ優先探索・最短経路探索・最小スパニング木・サブグラフと連結成分“でも述べたグラフのオイラー路(グラフの全ての辺を通る路)の問題で有名なケーニヒスベルクの橋がかかっている川の名前でもある。

GoogleのPregel論文は、グラフ並列計算に対する「頂点のように考える」アプローチを普及させたものとなる。Pregelのモデルは、基本的に、スーパーステップと呼ばれる一連のステップに編成されたグラフの頂点間のメッセージパッシングを使用する。各スーパーステップの最初に、Pregelは各頂点上でユーザー指定の関数を実行し、前のスーパーステップでその頂点に送られたすべてのメッセージを受け渡す。頂点関数は、これらのメッセージのそれぞれを処理し、他の頂点に順番にメッセージを送信する機会を持つ。また、頂点は計算を「停止させる投票」をすることができ、すべての頂点が停止に投票すると、計算が終了する。

• Clojure Glitteringを用いたPagerankによるネットワーク解析

前回”Clojureを用いたGraphX Pregelでのネットワーク解析“で分析したコミュニティのうち、何が最も大きなコミュニティを結びつけているのかを明らかにすることができるかどうかについて述べる。そのためには、さまざまな方法が考えられる。ツイートそのものにアクセスできれば、クラスタリングで行うようなテキスト分析を行って、これらのグループの間で特定の単語や特定の言語がより頻繁に使用されているかどうかを確認することもできる。

ここでは、ネットワーク分析について述べる。そこでは、グラフの構造を使って、各コミュニティで最も影響力のあるアカウントを特定する。これは例えば、最も影響力のあるアカウントのトップ10のリストは、そのフォロワーに何が共鳴しているかを示す指標になる。

• D3やReactを用いたナレッジグラフ(関係データ)の可視化

グラフデータ等の関係データを可視化するツールとしてJavascriptをベースとしたD3.jsやReactを利用したものを用いることができる。今回はグラフ表示形態として2D、3Dのグラフ表示および、関係データの表示形態としてヒートマップのそれぞれに対して、主にD3やReactでの具体的な実装について述べる。

• タイムライン上でグラフスナップショットを表示したり、アニメーション化する手法

タイムライン上でグラフスナップショットを表示したり、アニメーション化することは、時間的な変化を視覚化し、グラフデータの動的な特性を理解するのに役立ち、グラフデータを解析する上で重要な手法となる。ここではこれらに用いられるライブラリ及び実装例について述べている。

グラフニューラルネットワーク

グラフニューラルネットワーク(GNN)は、グラフデータに深層学習を適用するもので、データから特徴を抽出し、その特徴表現をもとにニューラルネットワークを構成し、それらを多段に繋ぎ合わせることで、複雑なデータパターンを捉え、非線形性を持つモデルを構築するものとなる。

通常の深層学習とグラフニューラルネットワークとの相違点は、一般的な深層学習は、画像データやテキストデータなどをグリッド状のデータ構造にして、行列演算アルゴリズムをベースに計算しているのに対して、GNNはグラフ構造に特化しており、ノードとエッジの組み合わせで表されるデータを計算しているところにある。

本ブログでは 以下のページにて、このGNNのアルゴリズム、実装例及び各種適用事例について述べている。

基本的なグラフデータアルゴリズム

• グラフネットワークアルゴリズムの基礎
• グラフ理論入門
• 複雑ネットワークとは何か 複雑な関係性を読み解く新しいアプローチ 読書メモ

「友だちの元カレは私の元カレだった！」たった6人をたどるだけで世界中の誰にでも行き着けるスモールワールド。「複雑ネットワーク」は21世紀最大のキーワード。複雑に見える身の回りの現象も「複雑ネットワーク」の考え方を応用すれば単純な関係に置き換えることができる。伝染病やコンピューター・ウイルスの感染経路、ニューロンやタンパク質の情報伝達の方法、会社や社会の中の人間関係に「意外な法則」が見えてくる

• Clojureを用いたネットワーク解析(1) 幅優先/深さ優先探索・最短経路探索・最小スパニング木・サブグラフと連結成分

グラフを視覚的な意味ではなく、数学的な意味で扱った場合について考える。グラフとは、単に辺で結ばれた頂点の集合であり、この抽象化の単純さは、グラフがどこにでもあることを意味する。グラフは、ウェブのハイパーリンク構造、インターネットの物理構造、道路、通信、社会的ネットワークなど、さまざまな構造の有効なモデルとなる。

これらのグラフデータの為のアルゴリズムに対して、以前”グラフデータの基本的アルゴリズム(DFS、BFS、ニ部グラフ判定、最短路問題、最小全域木)”や”高度なグラフアルゴリズム(強連結成分分解、DAG、2-SAT、LCA)”等でC++を使った実装について述べた。今回はClojure/loomを使った活用について述べる。

• グラフクラスタリング(外部リンク)
• グラフデータの基本的アルゴリズム(DFS、BFS、ニ部グラフ判定、最短路問題、最小全域木)

グラフデータの基本的アルゴリズム(DFS、BFS、ニ部グラフ判定、最短路問題、最小全域木)について述べる。まず深さ優先探索(DFS:Depth-First Search)について。DFSとは、探索の手法の一つとなる。ある状態からはじめ、遷移できなくなるまで状態を進めていき、遷移できなくなったら一つ前の状態に戻ると言うことを繰り返して解を見つける。幅優先探索(BFS:Breath-Fisrt Search)も基本的な探索の手法の一つとなり、深さ優先探索と同じく、ある状態からはじめて辿り着けるすべての状態を探索するものとなる。深さ優先探索と異なる点は探索する順番で、幅優先探索では、はじめの状態に近いほうから探索する点にある。

「ニ部グラフ判定」は頂点nの無向グラフが与えられ、隣接している頂点同士が違う色になるように、頂点に色を塗っていき2色以内ですべての頂点を塗ることができるかどうかを判定する。最短路問題はグラフの最も基本的な問題となる。最短路とは2頂点が与えられたときに、その頂点を始点・終点とするようなパスのうちで、通る辺のコストを最小にするもののことをいう。コストを距離として、最短距離を考えるとわかりやすい。無向グラフが与えられたときに、その部分グラフで任意の2頂点を連結にするような木を全域木(spanning tree)と呼ぶ。辺にコストがある時ら、使われる辺のコストの和を最小にする全域木を最小全域木(MST;Minimum Spanning Tree)と呼ぶ。

• 高度なグラフアルゴリズム(強連結成分分解、DAG、2-SAT、LCA)

有効グラフの頂点の部分集合Sが「任意の2頂点u,vをとったとき、uからvに到達できる」という条件を満たしている時、Sは強連結であると言う。頂点の強連結な集合Sに、他のどの頂点集合を付け加えても強連結にできないとき、Sを強連結成分(SCC:Strongly Connected Component)と言う。どんな有向グラフもいくつかの強連結成分の、共通部分をもたない和集合に分解することができる。これを強連結成分分解と呼ぶ。強連結成分を一つの頂点につぶすことで、DAG(閉路を持たない有向グラフ)となる。

論理式が与えられた時に、その論理変数に適切に真偽値を割り振ることによって、全体の真偽値を真とすることができるかを判定する問題を充足可能性問題(SAT)という。SATを解くことは一般にはNP完全だが論理式の形に制約がある場合には効率的に解くことも可能となる。

根付き木に対し、その頂点u,vの共通の祖先で最も近いところにあるものをuとvのLCA(Lowest Common Ancestor)と言う。LCAを効率的に求める手法にはさまざまなものがあるが、ここでは2種類の方法について述べる。

• ネットワークフロー問題のアルゴリズム

最大流・最小費用流などを中心に、グラフ状の流れ(フロー)について述べる。フローにはさまざまな性質や応用があり、広く活用されている。今回は、Ford-Fulkersonのアルゴリズムによる最大通信量問題の解決と最小カット問題との関係、最大流問題の特殊ケースであるニ部グラフの最大マッチング問題、一般マッチング問題と最小費用流問題について述べる。

• 最大流とグラフカット(1) 最大量と最小s-tカット

劣モジュラ関数は効率的に最小化が行える。特に有向グラフのカット関数の最小化は、最大流アルゴリズムで行えるため、理論的/実用的に高速な計算が可能となる。ここでは最大流アルゴリズムの基本的事項と、そのような計算へ帰着される例として、マルコフ確率場での推論を取り上げ、実用的にもよく用いられる、高速に計算可能な劣モジュラ関数のクラスについて述べる。

グラフカットは、数万〜数百万のオーダーの問題に対しても実用的時間で適用可能なアルゴリズムであると知られているが、劣モジュラ関数の観点から見ると、おおよそ2次の劣モジュラ関数ともいえるカット関数の最小化を行なっているものと解釈できる。カット関数の最小化に関しては、最大流アルゴリズムと呼ばれる理論的/実用的に高速なアルゴリズムの適用が可能であることがしられている。このようなカット関数の最小化として記述できるかどうかは、実用的に組み合わせ計算を行うことができるかどうかをはかる一つの見方であるともいえる。

ここではこのような関係を理解するために、まずカット関数の最小化とネットワークにおける最大流の計算との関係、そして実際に最大流計算を行う具体的な方法について見ていく。

• 最大流とグラフカット(2)最大流アルゴリズム

今回は、最大流を求める代表的なアルゴリズムであるフロー増加法について述べ、さらに最大流アルゴリズムを用いた最小s-tカットの計算方法や最大流最小カット定理の証明について述べる。さらフロー増加法とは異なる原理に基づく、高速な最大流アルゴリズムであるブリフロー・ブッシュ法についても述べる。

• 最大流とグラフカット(3) マルコフ確率場における推論とグラフカット

多変数データを扱う際に、データの各変数が何らかの構造を持つ場合、その構造を用いてさまざまな推論アルゴリズムが再帰的に記述できる場合がある。マルコフ確率場はその代表的なモデルで、無向グラフを用いて変数間のマルコフ性を表す。ここでは、マルコフ確率場の最大事後確率推定(maximum-a-posteriori estimation)と列劣モジュラ最適化との関係について述べる。さらに、コンピューター・ビジョン分野などでさかんに用いられているグラフカットは、本質的には、s-tカットの最小化計算をしていると言うことについて述べる。

• 最大流とグラフカット(4)グラフ表現可能な劣モジュラ関数

ここまで述べた様に、有向グラフのs-tカット関数は、高速な最小化が可能な劣モジュラ関数の特殊クラスであるといえる。しかし、当然ながら、この関数のみではその記述力に限界があるため、さまざまな実用的な場面で十分であるとは言えない。したがって、有向グラフのs-tカット関数よりも記述力があり、一方でこの関数同様に高速に最小化できる関数が考えられれば、実用上極めて有用になる。ここでは、その答えの一つとして、グラフ表現可能な劣モジュラ関数(graph-representable submodular function)について述べる。グラフ表現可能な劣モジュラ関数としては、いくつかの補助的な頂点を加えれば有向グラフのs-tカット関数として表すことができる関数で、先述した様な実用上有用な関数のクラスであると言える。

次に、有向グラフのs-tカット関数最小化のための最大流計算を行う方法として、プリフロー・プッシュ法について述べる。前述の様に、最大流については、最近オルリンによる計算量O(nm)のアルゴリズムが提案されている。プリフロー・プッシュ法の場合、計算量はO(mnlogn²/m)ではあるが、実用的には高速な実装が知られており、依然応用上重要なアルゴリズムとなる。また、この方法はパラメトリック最適化へも拡張できるため、後述においても重要な役割を果たす。

実行可能フローは「容量制約」と「流量保存制約」の両方を満たす様なフローξ=(ξ_e)_e∈ℰであった。プリフロー・プッシュ法では、実行可能フローの代わりに、流量保存制約を緩和して得られるプリフロー(preflow)と呼ばれるフローを考え、このプリフローが流量保存速を徐々に満たしていくように反復的に更新し、最終的に実行可能フローを得ることで最大流を計算する。

• 決定木アルゴリズム(1) 概要

決定木学習器は、フューチャーとして得られる可能性のある結果の関係をモデリングするために、木構造(tree structure)を使う強力な分類器となる。

決定木アルゴリズムの大きな特徴は、フローチャート風の木構造が必ずしも学習器内部専用になるわけではなく、モデルの出力結果を人間が読んで、特定のタスクのためにモデルが上手く機能する(あるいはしない)理由やメカニズムについて大きなヒントになるところにある。

このような仕組みを用いることで、法的な理由で分類メカニズムが透明なものでなければならない場合や、組織間での商慣行を明示するために他者と結果を共有する場合に特に有効になる。

• 決定木アルゴリズム(2) Rでのクラスタリング

今回はRを使った決定木のクラスタリングについて述べる。

利用するデータはハンブルグ大学の機械学習データレポジトリよりダウンロードするBank Marketing Data Setのbank.zipを用いる。このデータの中にはドイツの金融信用調査のデータが格納されている。

• 決定木アルゴリズム(3) ルール抽出

分類ルールは、ラベルの付けられていないインスタンスにクラスを与える論理if-else文という形で知識を表現する。これらは「前件(antexedent)」と「後件(consequent)」として指定され、「これが起きたら、あれが起きる」という仮説を形成する。単純な規則は「ハードディスクがカチカチ音を立てているなら、まもなくエラーを起こす」のように主張する。前件はフィーチャー値の特定の組み合わせから構成されるのに対し、後件は規則の条件が満たされたときに与えられるクラス値を指定する。

分類ルール学習は、決定木学習と同様に使われることが多い。分類ルールは具体的には次のような将来の行動のための知識を生成するアプリケーションで使える。(1)機械装置のハードウェアエラーを引き起こす条件の識別、(2)顧客セグメントに属する人々のグループの主要な特徴の記述、(3)株式市場の株価の大幅な下落、または上昇の前触れとなる条件の抽出

• 決定木アルゴリズム(4) Rでのルール抽出

今回はRを使った決定木によるルールの抽出について述べる。

ルールを抽出するデータとしては前回と同様にUCIレポジトリより、きのこが食べられるか?毒か?を判定するルールを抽出するデータを用いる。

• 決定木とオントロジー

今回は、多くの正しいアラインメント（正例）と正しくないアラインメント（負例）を提示することで、アラインメントのソート方法を学習するアルゴリズムについて説明する。これらのアプローチの主な違いは、本項の技術が学習のためにいくつかのサンプルデータを必要とすることにある。これは、アルゴリズム自身が提供し、判断対象となる対応関係のサブセットのみを用意するなどして、ユーザーが判断することもできるし、外部のリソースから持ってくることもできる。

• トポロジカルソート(外部リンク)

トポロジカルソートとは？
次の性質を持つ頂点の並び 𝑣1, 𝑣2, … , 𝑣𝑛
– すべての辺 𝑣𝑖, 𝑣𝑗 に対して、 𝑖 < 𝑗 が成立
– 言い換えると、すべての辺がその順序で”順方向”に向く

グラフデータの可視化技術

• D3やReactを用いたナレッジグラフ(関係データ)の可視化

グラフデータ等の関係データを可視化するツールとしてJavascriptをベースとしたD3.jsやReactを利用したものを用いることができる。今回はグラフ表示形態として2D、3Dのグラフ表示および、関係データの表示形態としてヒートマップのそれぞれに対して、主にD3やReactでの具体的な実装について述べる。

機械学習技術との組み合わせの理論

• スパースモデリングの概要と適用事例及び実装

スパースモデリングは、信号やデータの表現においてスパース性(疎な性質)を利用する手法となる。スパース性とは、データや信号において非ゼロの要素がごく一部に限られている性質を指す。スパースモデリングでは、スパース性を活用してデータを効率的に表現し、ノイズの除去、特徴選択、圧縮などのタスクを行うことが目的となる。

ここではこのスパースモデリングに関して、Lasso、コンプレッション推定、Ridge正則化、エラスティックネット、Fused Lasso、グループ正則化、メッセージ伝搬アルゴリズム、辞書学習等の各種アルゴリズムの概要と、画像処理、自然言語処理、推薦、シグナル処理、機械学習、信号処理、脳科学等の様々な適用事例に対する実装について述べている。

• グラフィカルモデル(1) ベイジアンネットワーク

グラフィカルモデルとは確率モデルをグラフを用いて記述したものとなる。確率モデルは、機械学習の中で扱う事象に、「不確実性」を導入したものでそれらは本質的に揺らぐものもあり、また単純に情報が不足している為に起こるものもある。

確率モデルの基本コンセプトは、それら不確実性を持った事象(確率変数)の間を関係性を示した辺で繋いでグラフにするもので、深層学習の始まりに登場した制約つきボルツマンマシン、混合ガウス分布やナイーブベイズもグラフィカルモデルの一種となる。これらは機械学習の複雑なモデルを表すシーンで多く活用されている。

• グラフィカルモデル(2) マルコフ確率場

ベイジアンネットワークは、ある確率変数が別の各確率変数について決める確率場であったが、マルコフ確率場では其々の確率変数が相互に関係し合っているモデルとなる。

マルコフ確率モデルの最もシンプルなものはイジングモデル(Ising model)と呼ばれるものとなる。これは物理の世界で磁性体についてのモデルとして用いられているもので、格子状にスピンと呼ばれる±の値を取る量があり(スピンが上を向いているものが+1、下を向いているものが-1)、以下に示すようなものとなる。

• 対称関係データのクラスタリング スペクトラルクラスタリング

スペクトラルクラスタリング(spectral clustering)は、対象関係データ(無向きかつ単一ドメインの関係データ)のオブジェクトクラスタリングの代表的な手法となる。この手法は主にコミュニティ抽出(community detection)のタスクに適用されるものとなる。ここでコミュニティとはそのクラスタ内ではオブジェクト同士が密に結合し、別のクラスタのオブジェクトとは非常に疎な結合をするクラスタのことで、密結合クラスタ(assortative cluster)とも呼ばれる。また、逆にクラスタ内で疎な結合を持ち外部と密な結合を持つクラスタを蘇結合クラスタ(disassortative cluster)と呼ぶ。

• 非対称関係データのクラスタリング技術 – 確率的ブロックモデルと無限関係モデル

確率的ブロックモデル(Stochastic Block Model:SBM)の目標は「非対称データに対しても適用可能で、かつ密結合クラスタ以外も抽出可能な関係データクラスタリング」となる。ここでSBMでは「潜在的なブロック構造」の存在を仮定する生成的な「確率モデル」によるアプローチを行う。

• 行列分解 -2つのオブジェクト間の関係構造の抽出

まず行列分解の例として「顧客が行、映画が列で、要素の値が評価値になる映画推薦」のタスクを考える。Netflixのような膨大な数のユーザーがいる場合、この行列をそのままの規模で保管し処理することは困難となる。この課題への解決策としてデータの圧縮がある。

• 高次関係データ -テンソルデータ処理の概要

今回は3つ以上のオブジェクトの関係について述べる。例として、映画をの評価を「顧客、映画、時間」の3項関係として表現することを考える

その他の例としては、気象データとして地球上の場所を緯度と経度で表し、観測地点ごとに風速、気温、湿度といったさまざまな計測をおこなって集めた「緯度、経度、計測」を分析するものや、言語データとしては複数の文書に対して、一つ一つの文章の中の主語、動詞、目的後の3つの組みの頻度を数えることで「ある動詞はある主語や目的語と一緒に出現しやすい」といった情報を得ることもできる。

• テンソル分解– CP分解とタッカー分解

テンソル分解は行列に比べると要素数が増えやすい性質をもっている。すべてのモードの次数が同じ場合(I=J=K>1)を考えると、行列は要素数がI²なのに対し、3次のテンソルはI³、L次のテンソルはI^Lとなる。このように次数が高くなればなるほど、Iが小さくても要素数が急激に増えることがわかる。このような大規模性をうまく扱うには、直感的に考えると、行列分解で見てきた次元圧縮の考え方が使える。

簡単のためにテンソルの字数は3とし、データとしてIxJxKの大きさを持つテンソルχが与えられたとする。行列における次元圧縮では行列の各行ベクトルがより低次元の空間で表現されることを仮定した。テンソルにおいては「行ベクトル」に対応するものとして「モード1スライス」を考える。そうするとテンソルにおける次元圧縮とし「各モード1スライスが低次元空間のベクトルとして表現されること」として捉えられる。ここで「モード1スライス」は行列なので、この次元圧縮を考えるにはベクトルから行列への写像が必要となる。

• ガウス過程回帰による異常検知 -入力に対する出力異常検知、実験計画法への適用

入力と出力の対が観測できる系に関する異常検知技術について述べる。この場合、入力と出力の関係を、応答曲面(ないし回帰曲線)という形でモデル化し、それからの外れという形で異常を検知する。実用上、しばしば入力と出力の関係は非線形となる。今回は、非線形回帰技術のうちで工学的に応用範囲の広いガウス過程回帰の手法について述べる。

入力と出力の双方が観測されている場合、最も自然な異常検知の方法は、与えられた入力に対して出力を眺めて、それが通常の振る舞いにより期待される値から大幅にずれているかどうかを見る、というものになる。この意味でこの問題を応答異常(response anomaly)検知問題と呼ぶこともできる。

• 部分空間法による変化検知 -時系列データのための特異スペクトル変換法

時系列データを念頭に変化検知問題について述べる。単一の標本の異常度を計算するだけでは変化検知はできない。ここではまず複数の異常度ないし標本を束ねるための基本技術として、累積和とスライド窓という考え方について述べ、それに基づき、変化検知を、逐次密度推定問題として抽象的に定式化する。その最も簡単な具体例として、特異スペクトル変換法という変化検知の手法について述べる。特異スペクトル変換法はその汎用性、ノイズに対する頑健性から実用上最も重要な変化検知法の一つとなる。

まず変化検知の古典技術である累積和法について述べる。例として、ある化学プラントの反応機の中での特定の化学物質の濃度を、時事刻々監視しているとする。化学物質は流体として出入りがあるので、たまたま局所的に濃度が濃くかったり高かったりするのは避けられず、この場合は、ホテリングのT2法のような「観測1回ごとにひとつひとつ異常度を計算する」タイプの監視技術は不適切となる。この場合やりたいことは、単発で突発的に異常値が得られたというよりは、継続して何かの異常事態が発生しているかどうかを検知すること、すなわち変化検知となる。

• 関係性へのスパース性の導入

データがスカラーの出力yとM次元ベクトルxの組でD={(y⁽ⁿ⁾,x⁽ⁿ⁾)|n=1,…,N}のように与えられている時、線形回帰としてスパースな解を実現する(回帰係数をスパースにしたり、変数ではなく、余分な標本を消すと言う意味でのスパース化を行う)ことについて述べる。

ユースケースとしては観測データがノイズで汚染されており、必ずしもすべての標本が信用できないと言う場合や、グラフデータに拡張して、ある機械を決まった数のセンサーで常時監視するような場合等のグラフモデル(関係モデル)への適用について述べる。

• グラフニューラルネットワーク(1) 概要

グラフデータに対して深層学習を行うフレームワークであるグラフニューラルネットワーク技術の概要。化合物の物性推定やAtttensionを使った自然言語処理、共起ネットワーク、画像情報処理等に活用される

• 機械学習の連続最適化としての準ニュートン法(2)記憶制限付き準ニュートン法

準ニュートン法は、ニュートン法におけるヘッセ行列の計算を回避し、効率的に最適化を行うための手法となる。今回は代表的なアルゴリズムを概観し、正定値行列空間上の幾何構造との関連を述べ、ヘッセ行列の疎性を利用する方法についても述べる。

知識グラフ等への応用

• ナレッジグラフの概要と国際学会(ISWC)での関連発表のまとめ

ナレッジグラフ（Knowledge Graph）とは、情報をグラフ構造で表現したものであり、人工知能（AI）の分野において重要な役割を果たすものとなる。ナレッジグラフは、複数のエンティティ（例えば人、場所、事物、概念など）が、その間の関係性（例えば「AがBを所有する」、「XはYの一部である」、「CはDに影響を与える」など）を持っているという知識を表現するために使用される。

具体的には、ナレッジグラフは、検索エンジンの質問応答システムや、人工知能の対話システム、自然言語処理の分野において重要な役割を果たしている。これらのシステムは、ナレッジグラフを利用して、複雑な情報を効率的に処理し、ユーザーに正確な情報を提供することができる。

• RDF技術概要

RDF(Resource Description Framework)は、以前LODでも述べた、ウェブ上にあるリソースのメタデータを技術する枠組みであり、W3Cにより1992年2月に規格化されたものとなる。

RDFの構造としては、トリプルデータのモデルがベースとなる。これは主語(subject)、述語(predicate)、目的後(object)の3つの要素でリソースに関する関係情報を表現したものとなる。

• オントロジーのグラフパターンマッチング

複合的な類似性の計算は、ノードの近隣を考慮して類似性を提供するだけなので、まだ局所的なものとなる。しかし、類似性はオントロジー全体を対象としており、最終的な類似性の値は、最終的にすべてのオントロジーエンティティに依存する可能性がある。さらに、オントロジーが有向非環状グラフに還元されていない場合、局所的な方法で定義された距離は、循環的に定義される可能性がある。これは最も一般的なケースである。例えば、2つのクラス間の距離が、そのクラス間の距離に依存するインスタンス間の距離に依存する場合や、オントロジー内に循環が存在する場合などに発生する。下図に示すように、ProductとBookの類似性は、hasProviderとhasCreatorおよびauthor、publisher、translatorの類似性に依存している。そして、これらの要素間の類似性は、最終的にProductとBookの類似性に依存する。この2つのグラフは、様々な意味でホモ・モルフィックとなる。

• オントロジーのメレオロジックなグラフパターンマッチング

Taxonomic(分類学的な)構造の次によく知られている構造は、mereologic(部分と全体)構造、つまり、part-of関係に対応する構造となる。BookとVolumeという2つのクラスが等価であることがわかり、それぞれInBookとBookChapterというクラスとの間にmereologicな関係がある場合、この2つのクラスは同様に関係している可能性があることを示唆している。この推論は部分から全体という逆の方向にも当てはまる。これは、個別の部分がある場合、つまりジャーナルIssueの部分がeditporial、article、recesions、lettureに区別される場合としてある。
このような構造を扱う上での難しさは、単なる構造を持つプロパティを見つけるのが容易ではないことなる。例えば、ProceedingsクラスはInProceedingsクラスといくつかのwhole-part関係を持つことができるが、それはproperties communicationsによって表現されるものとなる。これらのInProceedingsオブジェクトは、今度はセクションプロパティで表現される単なる構造を持つことになる。

• 自然言語のグラフ表現とベクトル表現

自然言語の文章が何らかの情報、すなわち意味を伝達している、ということは多くの人が認めている事実となる。ところが「意味とは何ですか」「コンピューター上で(あるいは数学の言葉で)どの様に定義しますか」と問われると、自然言語の専門家であってもはっきりと答えられる人はほとんどいない。自然言語の意味とは、存在することはほぼ確実だが、誰も見たことがないダークマターのようなものとなる。

• 知識グラフの質問応答システムへの応用

知識グラフとは、「エンティティとその間の関係を記述して作成したグラフ」と定義することができる。ここでの「エンティティ」とは物理的または非物理的に「存在する」もので必ずしも物質的な存在ではなく、抽象化されて事物(数学や法律、学問分野などの事象)を表す。

知識グラフの例としては、「テーブルの上に鉛筆がある」「富士山は静岡県と山梨県の境にある」というような単純で具体的なものから、「a=b なら、a+c = b+cである」「消費税とは、物品やサービスの「消費」に着目し課税する間接税である」「電子制御式燃料噴射装置において、吸気マニホールドのコレクターに取り付けられ、吸入空気量を制御するスロットルバルブを内蔵した吸気絞り装置をスロットルチャンバーと呼ぶ」のような抽象的なルールや知識を表したものまで多種多様にある。

  これらの知識グラフを用いることで、AIの観点からは知識グラフというデータを通じて機械が人間世界のルールや知識、常識等へのアクセスできるようになるという利点が生じる。AIが処理したデータを知識グラフと繋げることで、近年の深層学習をはじめとしたブラックボックス的なアプローチでの、「何を根拠に判断しているのか分からない」といった問題や、学習の精度を得るために大量の教師データが必要になるといった問題に対して、AIが処理した結果を人間にとって解釈しやすい表現にしたり、知識データを元にAIがデータを生成することでスモールデータでの機械学習が可能となる。

この知識グラフを質問応答システムに適用することで、単純なFAQの質問・回答ペアではなく、主要なタームの階層構造を作成し、更にコンテキストに応じた質問及びその代替語、同義語、機械学習応答のクラスなどと関連づけことができ、インテリジェントなFAQ体験を提供することが可能となる