グラフニューラルネットワーク

機械学習技術 人工知能技術 深層学習技術 自然言語処理技術 セマンティックウェブ技術 知識情報処理 オントロジー技術 AI学会論文集を集めて デジタルトランスフォーメーション技術 Python 本ブログのナビ

グラフニューラルネットワークの特徴と適用事例

概要

“グラフデータ処理アルゴリズムと機械学習/人工知能タスクへの応用“でも述べているグラフデータとは、頂点（ノード）とそれらを結ぶ辺（エッジ）からなるデータ構造を指す。これらは、ソーシャルメディアの友人関係、フォロワー関係、コミュニティ、交通ネットワーク、コンピュータネットワーク、ゲノムやタンパク質の相互作用ネットワーク、顧客の過去の購買履歴や嗜好などさまざまなネットワークデータを表し現実世界のさまざまなシステムや関係をモデル化するのに役立てられている。

グラフニューラルネットワーク(GNN)は、このようなグラフデータに深層学習を適用するもので、データから特徴を抽出し、その特徴表現をもとにニューラルネットワークを構成し、それらを多段に繋ぎ合わせることで、複雑なデータパターンを捉え、非線形性を持つモデルを構築する。

通常の深層学習とグラフニューラルネットワークとの相違点はデータ構造とそれらを扱うアルゴリズムにある。

一般的な深層学習では、画像データやテキストデータなどを規則的な均一のグリッド状のデータ構造にして、行列演算アルゴリズムをベースに計算している。それに対して、グラフデータでは、ノードに多くの隣接ノードを持つものとそうでないものがあり、隣接頂点が可変で均一なデータ構造は作りずらい。さらにトポロジーが複雑で非常に離れているノードがエッジで結合していることがあり、局所性が保たれないことや、ノードが順序づけられていない等も大きく異なる。

データを扱うアルゴリズムの観点では、一般的な深層学習では、ベクトルで代表される非構造データを用いて、分類、回帰、クラスタリング、次元圧縮等のタスクすべてに適用することができるが、グラフデータでは、ノードを対象としたタスク(ノード分類)、エッジを対象としたタスク(リンク予測)、グラフを対象としたタスク(グラフ分類)、生成モデルとしてのタスク(グラフ生成)とそれぞれのタスクでデータ構造とアプローチが異なってくる。

例えばノード分類では、友人関係を表す社会ネットワークにおいて、グラフのノードを「人」、ノードを結ぶエッジを「友人関係」、各ノードの特徴はその人の属性(年齢、性別、職業等)とすると、ノードの分類には、そのノードの特徴だけでなく、近傍(友人)のノードの特徴も必要となり、ノードの特徴を近傍に伝搬させることによって各ノードの特徴を学習(表現学習)するというアプローチが行われている。

また、そのグラフが属するクラスを特定するグラフ分類では、例えば、化学化合物において、原子をノード、結合をエッジとして、各ノードの特徴(水溶性の有無や毒性の有無など)を求めるようなアプローチがとられている。

グラフが与えられた時に、エッジで結ばれるべきノードペアや、各ノードにおけるエッジが生じる確率を求めるタスクがリンク予測となるが、これは例えば、ソーシャルメディアにおける友人の推薦や、商品と購入ユーザーからなる2部グラフで商品の購入を予測するような使い方に適用される。

グラフ生成は、グラフにある特性が与えられた時に、その特性を持つ類似したグラフを生成するようなモデルを構築するタスクで、創薬などで、ある特性を持つ化学化合物のグラフ構造を数多く生成するモデルなどに適用される。

非構造データをベクトル化して、ベクトル間の類似度を”機械学習における類似度について“に述べているような各種手法で計算し、非構造データ間の類似度を推定するエンべディングの手法は”多言語エンベディングの概要とアルゴリズム及び実装について“に述べているように自然言語処理だけでなく、”マルチモーダル検索へのElasticSearchと機械学習の適用と実装“で述べている画像や音声のデータの横断検索システムにも適用されている。

GNNにおいても、グラフの各ノードの構造情報を低次元のベクトルとするグラフエンべディング(graph embedding)と呼ばれる手法が提案されている。この手法を用いることで、従来エッジによって表されていたノード間の距離をベクトル間の距離とすることで、計算コストを下げ、並列・分散アルゴリズムを適用した形で、ノード分類、ノードクラスタリング、グラフ可視化、リンク予測などりタスクに利用できるようになる。それらは”A Survey on Network Embedding“にまとめられている。

ノードエンべディングの利点は、多くのノード属性情報を加味した上での構造情報のベクトル化による学習を可能にし、深層学習のアルゴリズムの適用を容易にしているところにある。このようなノードエンべディングの適用タスクとしては、従来のグラフデータアプローチでは困難であったノードの属性情報を加味した構造情報の次元圧縮などがある。グラフエンべディング代表的な手法としては、後述するDeepWalk、LINE、node2Vec、GraRep、GCN、GraphSAGE、変分グラフオートエンコーダ(Variational Graph AutoEncoder)などがある。

既存の機械学習のアプローチのGNNへの適用として、もう一つ挙げられるのがグラフ畳み込みとなる。

一般的な画像認識における畳み込みは、フィルタと呼ばれるサイズの小さい矩形を入力画像上でスキャンさせながら、積和演算を行い、フィルタが表すパターンと類似したパターンが入力画像のどこにあるのか検出するもので、そのような畳み込みを組み合わせていくことで、個々の画像から構成される入力画像の局所的特徴や、さらに大域的特徴へと階層的に認織していくものとなる。

これをグラフに適用するには、格子状に規則的に存在するような(画素)データではなく、頂点の数が増減し、かつ局所的でないグラフデータに適用したデータ構造とアルゴリズムを用いる必要がある。それらのアプローチとしては(1)Spectralなグラフ畳み込みと、(2)Spacialなグラフ畳み込みの2つがある。

Spectralなグラフ畳み込みは、グラフラプラシアンの固有ベクトルによる空間への変換・逆変換を行うことで、信号処理でのフーリエ変換による周波数成分への変換を行うものとなる。これらの代表的なアプローチとしては、後述するChebNet、ChebyNet、GCN(Graph Convolutional Network)等がある。

Spacialなグラフ畳み込みは、個々のノードとエッジで結ばれた周囲のノードの属性情報を集める操作を、畳み込み演算とみなして表現の学習を行うもので、メッセージパッシングのグラフ畳み込みとも呼ばれているものとなる。代表的なアプローチとしては後述するPATCHY-SAN、DCNN(Diffusion-Convolutional Neural Network)、GraphSAGE等がある。

更に、Structural Deep Network Embedding(SDNE)や、Variational Graph Auto-Encoders(VGAE)に代表されるグラフオートエンコーダ、さらにGraph Attention Network(GAT)に代表されるEncoder-Decoderモデルをベースとしたattentionモデル、”Adversarial Attacks and Defenses on Graphs: A Review, A Tool and Empirical Studies“に報告されている敵対的攻撃モデル、そして、Temporal Convolutional Networks (TCN)、Spatio-Temporal Graph Convolutional Networks (STGCN)、Dynamic Graph Convolutional Neural Networks (DGCNN)、Dynamic Attributed Network Embedding framework(DANE)、Continuous-Time Dynamic Network Embeddings(CTDNE)、Causal Anonymous Walks(CAWs)、Dynamic Graph Embedding Model(DynGEM)、Dynamic REPresentations over dynamic graphs(DyREP)、JOint Dynamic user-Item Embedding model(JODIE)、Temporal Graph ATtention(TGAT)、DynamicTriadなどの動的なグラフ構造モデルもある。

以上をまとめるとグラフデータを深層学習するためには、以下のようないくつかの工夫が必要となる。

1. グラフ構造のキャプチャ:

隣接行列やエッジ特徴の利用: グラフニューラルネットワーク（GNN）では、隣接行列を使ってノードの隣接関係をキャプチャし、それに基づいて情報を伝播させている。また、エッジの特徴も活用して、異なるノード間の関係性を考慮することができる。

グラフのアトリビュートや構造情報: グラフには、ノードやエッジの属性（アトリビュート）や構造的な情報が含まれる。これらの情報を適切に利用することで、モデルの表現力を向上させることができ、たとえば、ノードの次数（degree）やクラスタ係数などのグラフレベルの特徴を考慮することが可能となる。

2. ノード表現の更新:

集約関数（Aggregation Function）の設計: ノードの隣接情報を集約する際に使用される関数は、グラフによって適切なものを選択する必要があり、例えば、平均プーリング、最大プーリング、LSTMセルなどを用いる。

隣接情報の利用: グラフ内のノードが持つ情報を利用して、各ノードの表現を更新する。典型的な手法には、隣接ノードの特徴を集約し、それを現在のノードの特徴と組み合わせる手法がある。

3. グラフの性質への対処:

グラフの可変長性: グラフは可変長の構造を持つため、異なるサイズのグラフに対応できるように設計する必要がある。これには、パディングやマスキング、動的なグラフプーリングなどがある。

局所性とグローバル性のバランス: グラフデータは局所的なパターンとグローバルな構造の両方を持っており、モデルは、これらの局所性とグローバル性の両方をうまく捉える必要がある。これには例えば、階層的なGNNの導入や、注意メカニズムの利用などがある。

4. モデルの設計:

グラフプーリングの導入: グラフが大きくなると、全てのノードを使って処理を行うのはコストが高い場合があり、そのため、グラフプーリング層を導入して、グラフを階層的に処理することがある。

リカレントニューラルネットワーク（RNN）との組み合わせ: グラフ構造内のシーケンスや時間依存性を考慮する場合、RNNとGNNを組み合わせることがある。

トランスフォーマーの活用: グラフデータの処理において、トランスフォーマー（Transformer）アーキテクチャを利用することもある。グラフ上の自己注意機構を活用して、ノード間の関係性を学習することができる。

5. データ拡張と正則化:

グラフのデータ拡張: 画像やテキストデータのように、グラフデータに対するデータ拡張も重要となる。これには、グラフのランダムな部分グラフの切り出しや、ノードの特徴のノイズの追加などが考えられる。

ドロップアウトやバッチ正規化: モデルの汎化性能を向上させるために、ドロップアウトやバッチ正規化などの正則化手法を適用することがある。

このようにグラフデータを用いることで、従来表せなかったようなデータ構造を表すことができ、さまざまな応用が検討されている。それらは「Graph neural networks: A review of methods and applications」などの論文に挙げられており、テキスト、画像、物理学、化学、生物学、交通網、推薦システム、組み合わせ最適化など多岐にわたる。

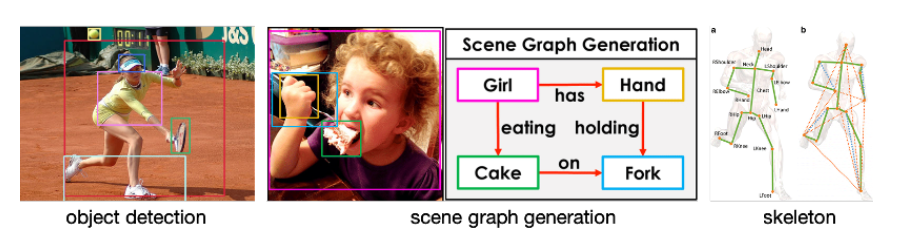
例えば、画像処理では画像に現れる対象間の関係を認織することで、ペットと飼い主の関係なのか、警察犬と追われる犯人なのかを識別したり、

推薦システムでは、ユーザーと商品をノード、購入という関係をエッジとして表し、入力がユーザーや商品としたときの、予測される購入(欠損したエッジ)を求めたり、

交通量予測では、道路をセグメントに分割してグラフとして表現し、各セグメントでのカメラから交通量及び距離を入力として、渋滞やスピードを予測したり、

ソフトウェア構造をグラフ化して解析/予測及び生成を行ったり

言語処理に適用して、文脈やコンテキストに合わせた解析/予測及び生成を行ったり

コンテキストの予測と異常検知を行ったり

あるいは近年のcovid-19との戦いでは、生体医療データ、疫学ネットワーク、サプライチェーンネットワークのデータを用いて、時空間グラフニューラルネットワークのアプローチの適用が行われていた。さらにGNNを用いた異常検知なども検討されている。

その他の適用事例については東工大の村田研のサイトや、参考文献”Graph Neural Networks: Foundations, Frontiers, and Applications“も参照のこと。

トピック

ガウス的世界と非ガウス的な世界のモデリング

ガウス的世界と非ガウス的な世界のモデリング。”機械学習における確率的アプローチ“でも述べている機械学習の確率的アプローチでは、ガウス分布から出発した様々な確率分布を用いて計算が行われている。このガウス分布(正規分布)は、カール・フリードリヒ・ガウス（Carl Friedrich Gauss） にちなんで名付けられたものだが、実は以下のように「最初に発見した」のはガウスではないと言われている。

脱構築とグラフニューラルネットワーク

脱構築とグラフニューラルネットワーク。哲学の世界においても、動的なフレームの変化に対応した考え方は提示されている。それらの一つは、ポスト構造主義と呼ばれるものとなる。ポスト構造主義は、静的なパターン認織では見ることができなかった動的な要素を、差異として認織していくことで、パターンの変化や、パターンから外れるもの、逸脱を問題にして、ダイナミックに変化していく世界を論じ、かつ人間の創造性のようなものを述べようとするものとなる。このアプローチは人工知能技術でいうとグラフニューラルネットワークの世界に近い考え方になる。グラフニューラルネットワークでは、そのものがもつエンべディングが特徴だけではなく、それらがつながる他の存在との関係性のトポロジーを組み込んで、そのものの特徴としている。

AGIと知識情報/グラフデータに関連する国際学会での論文

AGIと知識情報/グラフデータに関連する国際学会での論文。AGI（Artificial General Intelligence）とは、人間の知能に近い一般的な知能を持ち、様々なタスクに対応できるAIシステムのことである。現在のAIは、専用のモデルを用いて特定のタスクを得意としているが、AGIは多様なタスクを柔軟にこなすことを目指している。AIにおける知識情報処理は、膨大なデータを扱い、抽出、分類、推論、解釈などのタスクを行う。AGIはこれらの技術を統合し、人間の能力に近い複数のタスクを実行しようとしている。ノードとエッジでデータを表現するグラフデータは、AIにおいて関係やパターンを理解する上で極めて重要である。AGIは、グラフデータを効果的に利用して、大規模なデータセットから高度な知識を抽出することを目指している。このブログでは、グラフデータを用いた知識情報処理や機械学習の進歩に焦点を当てた、国際会議で発表された最近の論文に焦点を当てている。

知識表現と機械学習と推論とGNN

知識表現と機械学習と推論とGNN。“知識情報処理技術“で述べている知識表現と”推論技術“で述べている推論は、情報を構造化し、意味的な理解を促進するための重要な分野であり、これに対して、”グラフニューラルネットワーク“で述べているグラフ構造データの処理に特化した機械学習手法であるグラフニューラルネットワーク（GNN）を適用することは、知識表現と推論のタスクに対してより効率的かつ効果的なアプローチが可能になるものとなる。

各種グラフニューラルネットワークの実装

Graph Neural Networkの実装は主にpytorch等の深層学習のフレームワークを用いて行われている。以下に、それらの具体例について述べる。

GNNの基盤技術

pytorchの概要と環境設定及び実装例

pytorchの概要と環境設定及び実装例。PyTorchは、Facebookが開発しオープンソースで提供されている深層学習のライブラリであり、柔軟性、動的計算グラフ、GPU加速などの特徴を持ち、様々な機械学習タスクを実装を可能としてくれるものとなる。以下に、PyTorchを用いたさまざまな実装例について述べる。

グラフニューラルネットワークの概要と適用事例およびpythonによる実装例について

グラフニューラルネットワークの概要と適用事例およびpythonによる実装例について。グラフニューラルネットワーク(Graph Neural Network, GNN)は、グラフ構造を持つデータに対するニューラルネットワークの一種であり、グラフ構造を持つデータとは、要素間の関係を表現するために、頂点(またはノード)と、頂点間を結ぶエッジ(またはリンク)から構成されるグラフと呼ばれるデータ構造を使用して構築されたデータのことを指す。グラフ構造のデータの例としては、ソーシャルネットワーク、道路網、化学分子の構造、知識グラフなどがある。

ここでは、このGNNに関しての概要と様々な実施例およびPythonによる実装例について述べている。

Graph Neural Networks: Foundations, Frontiers, and Applicationsの概要

“Graph Neural Networks: Foundations, Frontiers, and Applications”の概要。Springerから2022年に出版された”Graph Neural Networks: Foundations, Frontiers, and Applications“の概要について述べる。

ランダムウォークの概要とアルゴリズム及び実装例

ランダムウォークの概要とアルゴリズム及び実装例。ランダムウォーク（Random Walk）は、グラフ理論や確率論で用いられる基本的な概念で、グラフ上のランダムな移動パターンを表現し、グラフ内の構造や特性を理解するのに役立つ手法となる。

機械学習におけるメッセージパッシングの概要とアルゴリズム及び実装例

機械学習におけるメッセージパッシングの概要とアルゴリズム及び実装例。機械学習におけるメッセージパッシングは、グラフ構造を持つデータや問題に対する効果的なアプローチで、特に、グラフニューラルネットワーク（Graph Neural Networks, GNN）などの手法で広く使用されている手法となる。

グラフニューラルネットワーク(1) 概要

グラフニューラルネットワーク(1)概要 。グラフデータに対して深層学習を行うフレームワークであるグラフニューラルネットワーク技術の概要。化合物の物性推定やAtttensionを使った自然言語処理、共起ネットワーク、画像情報処理等に活用される

基本アルゴリズム

グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）の概要とアルゴリズム及び実装例について

グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）の概要とアルゴリズム及び実装例について。グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）は、グラフ構造を持つデータに対する畳み込み演算を可能にするニューラルネットワークの一種であり、通常の畳み込みニューラルネットワーク（CNN）は、画像データなどの格子状のデータに対して効果的なものに対して、GCNは、グラフデータやネットワークデータのような非常に複雑な構造を持つ非格子状のデータに対する深層学習の手法として開発されたものとなる。

GNNにおけるエンコーダー/デコーダーモデルの概要とアルゴリズム及び実装例

GNNにおけるエンコーダー/デコーダーモデルの概要とアルゴリズム及び実装例。エンコーダー/デコーダーモデルは、深層学習における重要なアーキテクチャの1つで、このモデルは、入力シーケンスを固定長のベクトル表現にエンコードし、その後、その表現を使用してターゲットシーケンスを生成するためにデコードする構造となっている。グラフニューラルネットワーク（Graph Neural Networks, GNN）におけるエンコーダーとデコーダーモデルは、グラフデータから特徴表現（エンベディング）を学習し、その表現を用いてグラフ上のさまざまなタスクを解決するための枠組みとなる。

GNNにおける説明可能性の概要とアルゴリズム及び実装例

GNNにおける説明可能性の概要とアルゴリズム及び実装例。GNN(Graph Neural Networks)は、グラフ構造データを扱うためのニューラルネットワークであり、ノードとエッジ(頂点と辺)の情報を利用して、グラフデータ内のパターンや構造を捉え、ソーシャルネットワーク分析、化学構造の予測、推薦システム、グラフベースの異常検知などに適用される手法となる。

グラフニューラルネットワーク用いた反実仮想学習の概要と関連アルゴリズム及び実装例

グラフニューラルネットワーク用いた反実仮想学習の概要と関連アルゴリズム及び実装例。グラフニューラルネットワーク（GNN）を用いた反実仮想学習（counterfactual learning）は、グラフ構造を持つデータに対して「もし〜だったら」という仮定のもとで、異なる条件下での結果を推論する手法となる。反実仮想学習は因果推論と密接に関連しており、特定の介入や変更が結果に与える影響を理解することを目的としている。

GNNにおける敵対的攻撃モデルの概要とアルゴリズム及び実装例

GNNにおける敵対的攻撃モデルの概要とアルゴリズム及び実装例。敵対的攻撃(Adversarial Attack)は、機械学習モデルに対する攻撃手法の一つであり、特に画像やテキスト、音声などの入力データに対して広く用いられるものとなる。敵対的攻撃は、わずかな摂動(ノイズや操作)を加えることにより、機械学習モデルの誤認識を引き起こすことを目的としている。このような攻撃は、セキュリティの脆弱性を明らかにし、モデルのロバスト性を評価するのに役立つ

Deep Graph Infomaxの概要と実装例

Deep Graph Infomaxの概要と実装例。Deep Graph Infomax (DGI) は、グラフデータに対する無教師学習手法の一つで、ノード表現を学習するために 情報理論 に基づいた目標を設定するアプローチとなる。DGIは、グラフの局所的な特徴（ノードレベル）とグローバルな特徴（グラフレベル）を一致させることで、高品質なノード埋め込みを得ることを目的としている。

Graph Embedding (グラフ埋め込み)

グラフエンべディングの概要とアルゴリズム及び実装例

グラフエンべディングの概要とアルゴリズム及び実装例。グラフ埋め込み（Graph Embedding）は、グラフ構造を低次元のベクトル空間にマッピングすることで、グラフのノードやエッジを密な数値ベクトルで表現して、機械学習アルゴリズムによって処理したグラフ理論と機械学習を組み合わせたアプローチとなる。グラフ埋め込みの目的は、グラフ構造の情報を保持しながら、各ノードを密なベクトルで表現することであり、この表現を使うことでさまざまな情報を扱うことが可能となる。また、従来エッジによって表されていたノード間の距離をベクトル間の距離とすることで、計算コストを下げ、並列・分散アルゴリズムを適用した形で、ノード分類、ノードクラスタリング、グラフ可視化、リンク予測などりタスクに利用できるようになる。

GraphSAGEの概要とアルゴリズム及び実装例について

GraphSAGEの概要とアルゴリズム及び実装例について。GraphSAGE（Graph Sample and Aggregated Embeddings）は、グラフデータからノードの埋め込み（ベクトル表現）を学習するためのグラフ埋め込みアルゴリズムの一つであり、ノードの局所的な隣接情報をサンプリングし、それを集約することによって、各ノードの埋め込みを効果的に学習するものとなる。このアプローチにより、大規模なグラフに対しても高性能な埋め込みを獲得することが可能となる。

VERSEの概要とアルゴリズム及び実装例について

VERSEの概要とアルゴリズム及び実装例について。VERSE（Vector Space Representations of Graphs）は、グラフデータの埋め込みを学習するための手法の一つであり、グラフデータを低次元のベクトル空間に埋め込むことで、ノードやエッジの特徴を数値化し、機械学習アルゴリズムに適用するための表現を提供するものとなる。VERSEは特に大規模なグラフに対して高速で効果的な埋め込みを学習することができることで知られている。

Metapath2Vecの概要とアルゴリズム及び実装例

Metapath2Vecの概要とアルゴリズム及び実装例。Metapath2Vecは、グラフデータ上でのノードの表現学習に使用される手法の1つであり、この手法は、ノードの系列データから、各ノードの密なベクトル表現を学習するものとなる。Metapath2Vecは、特に異種グラフ（heterogeneous graph）やメタパス（metapath）と呼ばれるグラフ構造を扱う場合に有用なアプローチとなる。

HIN2Vecの概要とアルゴリズム及び実装例

HIN2Vecの概要とアルゴリズム及び実装例。HIN2Vec（Heterogeneous Information Network Embedding）は、異種情報ネットワークをベクトル空間に埋め込む手法で、異種情報ネットワークは、複数の異なる種類のノードやリンクで構成されるネットワークであり、例えばソーシャルネットワーク、推薦システム、情報検索などの分野でよく使用されるものとなる。HIN2Vecは、異種情報ネットワーク内の異なる種類のノードを効果的に表現することを目的としており、この手法は、グラフ埋め込み（Graph Embedding）と呼ばれる分野の一部であり、ノードを低次元のベクトルに埋め込むことで、ネットワーク構造やノード間の関係を保持することを目指すものとなる。

HIN2Vec-GANの概要とアルゴリズム及び実装例

HIN2Vec-GANの概要とアルゴリズム及び実装例。HIN2Vec-GANは、グラフ上の関係を学習するために使われる技術の一つで、具体的には、異種情報ネットワーク（Heterogeneous Information Network, HIN）上で埋め込みを学習するための手法として開発されたものとなる。HINは、異なる種類のノードとエッジを持つグラフ構造で、複雑な関係を持つデータを表現するために使われている。

HIN2Vec-PCAの概要とアルゴリズム及び実装例

HIN2Vec-PCAの概要とアルゴリズム及び実装例。HIN2Vec-PCAは、異種情報ネットワーク（HIN）から特徴を抽出するために、HIN2Vecと主成分分析（PCA）を組み合わせた手法となる。

LINE（Large-scale Information Network Embedding）の概要とアルゴリズム及び実装例について

LINE（Large-scale Information Network Embedding）の概要とアルゴリズム及び実装例について。LINE（Large-scale Information Network Embedding）は、グラフデータアルゴリズムの一種で、大規模な情報ネットワーク（グラフ）を効率的に埋め込むための手法となる。LINEは、ノード（ノードはグラフ内の個々の要素やエンティティを表します）の特徴ベクトル（埋め込み）を学習することを目的としており、これらの特徴ベクトルを使用することで、ノード間の関係や類似性をキャプチャし、さまざまなタスクに応用できるものとなる。

Node2Vecの概要とアルゴリズム及び実装例について

Node2Vecの概要とアルゴリズム及び実装例について。Node2Vecは、グラフデータのノードを効果的に埋め込むためのアルゴリズムの一つであり、Node2Vecは、Word2Vecと似たようなアイデアに基づいており、ノードの埋め込みを学習するためにランダムウォークを使用するものとなる。このアルゴリズムは、ノードの類似性や関連性を捉え、異なるグラフデータ関連のタスクに応用されている。

GraREPの概要とアルゴリズム及び実装例

GraREPの概要とアルゴリズム及び実装例。GraREP（Graph Random Neural Networks for Representation Learning）は、グラフ表現学習のための新しい深層学習モデルとなる。グラフ表現学習は、ノードとエッジから成るグラフ構造データから、それぞれの要素（ノードやエッジ）の表現を学習するタスクで、ソーシャルネットワーク、分子構造、コミュニケーションネットワークなど、さまざまな分野で重要な役割を果たしている。

Structural Deep Network Embedding(SDNE)の概要とアルゴリズム及び実装例

Structural Deep Network Embedding(SDNE)の概要とアルゴリズム及び実装例。Structural Deep Network Embedding(SDNE)は、オートエンコーダをグラフに拡張したグラフオートエンコーダーの一種となる。オートエンコーダーは、与えられたデータを潜在空間における低次元ベクトルにエンコードする教師なし学習を行うニューラルネットワークで、グラフオートエンコーダーでは、ノードの属性も利用するか、エンコーダーとデコーダーで何を使うか、何を目的関数とするかにより多くのバリエーションがある。SDNEはそれらの中で、1次の近接性と2次の近接性を同時に維持することを目的とした多層オートエンコーダー(Stacked AutoEncoder)となる。

Variational Graph Auto-Encoders(VGAE)の概要とアルゴリズム及び実装例について

Variational Graph Auto-Encoders(VGAE)の概要とアルゴリズム及び実装例について。Variational Graph Auto-Encoders (VGAE) は、グラフデータに対する”変分オートエンコーダ (Variational Autoencoder, VAE)の概要とアルゴリズム及び実装例について“でも述べているVAEの一種となる。

GAT (Graph Attention Network)の概要とアルゴリズム及び実装例について

GAT (Graph Attention Network)の概要とアルゴリズム及び実装例について。Graph Attention Network（GAT）は、グラフ構造に対する注意メカニズムを使用してノードの表現を学習する深層学習モデルとなる。GATは、異なるノード間の関係や接続パターンに基づいて、各ノードの重要度を自動的に決定することが可能なアプローチとなる。

グラフの特殊タイプ

メタパスを定義して非同質グラフの異なるエッジタイプを扱う方法について

メタパスを定義して非同質グラフの異なるエッジタイプを扱う方法について。メタパスは、異種グラフ内の異なるエッジタイプやノードタイプ間のパターンを表現するためのグラフパターンであり、異種グラフにおいて、異なるエッジタイプを扱うためには、それぞれのエッジタイプを表現するメタパスを適切に定義する必要がある。以下に、メタパスを定義して非同質グラフの異なるエッジタイプを扱う方法の一般的な手順を示す。

R-GCNの概要とアルゴリズム及び実装例

R-GCNの概要とアルゴリズム及び実装例。R-GCN（Relational Graph Convolutional Network）は、グラフデータ上で畳み込み演算を行うニューラルネットワークの一種となる。通常のグラフ畳み込み演算では、単一のグラフ構造を扱うが、R-GCNは異なる種類の関係（リレーション）を持つ多重グラフ（異種情報ネットワーク）に対して効果的に畳み込み演算を行っている。R-GCNは、異種情報ネットワーク内のノードの表現学習に適しており、さまざまなタスクに応用される。これは、異なる種類の関係を持つノードが多数存在する実世界のデータや問題に対応するために開発されたものとなる。

Lifted Relational Neural Networks (LRNN)の概要とアルゴリズム及び実装例

Lifted Relational Neural Networks (LRNN)の概要とアルゴリズム及び実装例。Lifted Relational Neural Networks（LRNN）は、関係データを扱うためのニューラルネットワークモデルの一種であり、関係データを表現し、関係推論を行うために設計されたものとなる。

KBGAT（Knowledge-based GAT）の概要と実装例

KBGAT（Knowledge-based GAT）の概要と実装例。KBGAT（Knowledge-based Graph Attention Network）は、知識グラフ（Knowledge Graph）を扱うために特化されたグラフニューラルネットワーク（GNN）の一種で、特に知識グラフのノード間の関係を効率的にモデル化するための手法となる。KBGATは、従来のGAT（Graph Attention Network）を基にして、知識グラフの特殊な構造を活かして設計されており、以下のような特徴がある。

Graph Isomorphism Network (GIN)の概要とアルゴリズム及び実装例について

Graph Isomorphism Network (GIN)の概要とアルゴリズム及び実装例について。Graph Isomorphism Network (GIN)は、グラフ構造の同型性を学習するためのニューラルネットワークモデルであり、グラフ同型性の問題は、2つのグラフが同じ構造を持つかどうかを判定する問題で、多くの分野で重要なアプローチとなる。

シミュレーションと物理学

物理シミュレーションに用いられるGraphNetworksの概要とアルゴリズム及び実装例

物理シミュレーションに用いられるGraphNetworksの概要とアルゴリズム及び実装例。物理シミュレーションにおけるGraph Networksの応用は、複雑な物理システムを効率的かつ高精度にモデル化するための強力な手法となる。

Graph Network-based Simulatorsの概要とアルゴリズム及び実装例

Graph Network-based Simulatorsの概要とアルゴリズム及び実装例。Graph Network-based Simulators（GNS）は、物理シミュレーションを行うための強力なツールで、グラフネットワークを用いて物理システムの動的挙動を予測するものとなる。GNSは、シミュレーションの精度と効率を向上させるために設計されており、複雑な相互作用を持つ多くの物理システムに適用することができる。

物理シミュレーションに用いられるInteraction Networksの概要と関連アルゴリズム及び実装例

物理シミュレーションに用いられるInteraction Networksの概要と関連アルゴリズム及び実装例。Interaction Networks（INs）は、物理シミュレーションや他の科学的応用に使用される、グラフ構造を持つデータ間の相互作用をモデル化するためのネットワークアーキテクチャとなる。INsは、物理法則やデータの相互作用をモデル化することができる。

MeshGraphNetsの概要とアルゴリズム及び実装例

MeshGraphNetsの概要とアルゴリズム及び実装例。MeshGraphNetsは、物理シミュレーションに特化したグラフニューラルネットワーク（GNN）の一種で、特にメッシュベースの表現を用いたシミュレーションに優れてたもので、MeshGraphNetsは、三角形や四面体といったメッシュ要素をグラフのノードとエッジとして表現し、その上で物理的なシミュレーションを行うことが可能な手法となる。

動的グラフ処理

時空間グラフ畳み込みネットワークの概要とアルゴリズム及び実装例

時空間グラフ畳み込みネットワークの概要とアルゴリズム及び実装例。時空間グラフ畳み込みネットワーク(STGCN: Spatio-Temporal Graph Convolutional Network)は、時系列データがノードとエッジで構成されるグラフ上にある時系列データを対象とした畳み込みであり、リカレントニューラルネットワーク(Recurrent Neural Network,RNN)の代わりに時間変化の予測に用いられるモデルとなる。これは、交通流や気象データなどのように、地理的な位置や時間的な変化が重要なデータに対して効果的なアプローチとなる。

ST-GCN (Spatio-Temporal Graph Convolutional Networks)の概要とアルゴリズム及び実装例について

ST-GCN (Spatio-Temporal Graph Convolutional Networks)の概要とアルゴリズム及び実装例について。ST-GCN（Spatio-Temporal Graph Convolutional Networks）は、動画データや時間的データを扱うために設計されたグラフ畳み込みネットワークの一種であり、グラフ構造を持つデータ（例: 隣接ノードとエッジで表現されるネットワークデータ）に対して、空間的な情報（グラフ内のノード間の関係）と時間的な情報（連続したフレームまたは時間ステップ）の両方を考慮して特徴抽出と分類を行うことができる手法となる。これは主に動画分類、動作認識、スポーツ解析などのタスクに用いられている。

動的グラフのエンべディングの概要とアルゴリズム及び実装例

動的グラフのエンべディングの概要とアルゴリズム及び実装例。“グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）の概要とアルゴリズム及び実装例について“で述べているグラフ畳み込み、”グラフエンべディングの概要とアルゴリズム及び実装例“で述べているグラフエンべディング、”Structural Deep Network Embedding(SDNE)の概要とアルゴリズム及び実装“に述べているグラフオートエンコーダ等では、主に静的グラフを対象にモデルを構築していた。それに対して、現実のデータでは動的なグラフで表される関係性が数多く存在しており、”時間と共に変化していくグラフデータを解析する手法について“に述べているようにさまざまなアプローチが行われている。

動的グラフのエンベディングを行うには、グラフの構造とその動的変化の両方を反映させたベクトル表現にする必要があり、動的グラフの表現方法としては以下の2つに分けられる。

ダイナミックグラフ埋め込みによる時間的な変化を考慮に入れるグラフデータ解析

ダイナミックグラフ埋め込みによる時間的な変化を考慮に入れるグラフデータ解析。ダイナミックグラフ埋め込み（Dynamic Graph Embedding）は、時間的な変化を考慮に入れるグラフデータ解析のための強力な手法となる。このアプローチでは、グラフデータが時間に沿って変化する場合、ノードやエッジの表現を時間軸上で持つことを目的としている。

生成系AIおよびデータ解析

生成系AIに向けたプロンプトの自動生成のアプローチについて

生成系AIに向けたプロンプトの自動生成のアプローチについて。生成系AIは、テキスト、画像、音声、動画などの新しいコンテンツを生成する人工知能技術を指す。生成系AI（例えば、画像生成AIやテキスト生成AI）は与えられた指示（プロンプト）に基づいて新しいコンテンツを生成するため、プロンプトの質や適切さがAIのパフォーマンスを最大限に引き出すカギとなる。

Deep Graph Generative Models（DGMG）の概要とアルゴリズム及び実装例

Deep Graph Generative Models（DGMG）の概要とアルゴリズム及び実装例。Deep Graph Generative Models（DGMG）は、グラフ生成タスクに特化したディープラーニングモデルの一種で、特に複雑なグラフ構造の生成に有効なアプローチとなる。DGMGは、グラフ生成プロセスを逐次的な決定問題として扱い、グラフのノードとエッジを順番に生成している。

LPAの概要とアルゴリズム及び実装例

LPAの概要とアルゴリズム及び実装例。LPA（Label Propagation Algorithm）は、グラフベースの半教師あり学習アルゴリズムの一種であり、このアルゴリズムは、グラフ上のラベル付きノードからラベルなしノードへのラベルの伝播を通じて、ラベルなしデータにラベルを付与することを目的としている。LPAは、ラベル伝播法としても知られている。

HARPの概要とアルゴリズム及び実装例について

HARPの概要とアルゴリズム及び実装例について。HARP（Hierarchical Attention Relational Graph Convolutional Network for Poverty Prediction）は、貧困予測のための階層的アテンション関係グラフ畳み込みネットワークとなる。この手法は、グラフ構造を持つデータ（例：都市の人口統計、地理的特徴、社会経済指標など）を使用して、貧困の予測を行っている。

アプリケーション

グラフニューラルネットワークを用いた建築構造設計の概要と関連アルゴリズム及び実装例

グラフニューラルネットワークを用いた建築構造設計の概要と関連アルゴリズム及び実装例。グラフニューラルネットワーク（GNN）を用いた建築構造設計は、建築物の構造を自動的に生成し、評価するための手法となる。

GNNを用いた材料の特性や構造をモデル化し、新しい材料の設計や特性予測を行うサービスの概要

GNNを用いた材料の特性や構造をモデル化し、新しい材料の設計や特性予測を行うサービスの概要。GNN(Graph Neural Networks)を用いた新しい材料の設計や特性予測を行うサービスは、材料科学の分野における研究開発の効率化、コスト削減、および新しい高性能材料の迅速な発見を目的としたものとなる。これはGNNを用いて材料の特性や構造をモデル化し、新しい材料の設計やその特性予測を支援する機能を持つ。

半導体技術とGNN

半導体技術とGNN。GNNは、グラフデータを扱うためのディープラーニング技術で、ノード（頂点）とエッジ（辺）で表現されるグラフ構造に対して、有向/無向の関係性を考慮しながら、ノードやエッジの特徴を学習するものとなる。このGNN技術は、ノード間の複雑な相互依存性を捉えることが可能で、様々な領域での適用が検討されており、半導体技術のさまざまな側面で応用できる強力な機械学習手法となっている。今回はGNNの半導体技術への具体的な応用例について述べる。

LIDAR（Light Detection and Ranging)と生成系AIとGNN

LIDAR（Light Detection and Ranging)と生成系AIとGNN。LIDAR（Light Detection and Ranging、ライダー）は、レーザー光を使用して対象物までの距離を測定し、周囲の環境や物体の3次元形状を高精度に把握する技術で、レーザー光を照射し、その反射を検知することで、対象物の距離や形状を測定するものとなる。この技術は、自動運転や地形測量、考古学、建設など、さまざまな分野で利用されている。

電力貯蔵技術とスマートグリッドとGNN

電力貯蔵技術とスマートグリッドとGNN。電力貯蔵技術は、電力を一時的に貯蔵し、必要なときに放出する技術の総称で、主に電力の供給と需要が一致しない場合や、再生可能エネルギー源の変動的な発電量を調整するために利用されるものとなる。この電力貯蔵技術を組み合わせると、以下に示すようなスマートグリッド内でのエネルギーの変動を調整を行うことが可能になる。

グラフニューラルネットワークを用いたアーバンインテリジェンスの概要と関連アルゴリズム及び実装例

グラフニューラルネットワークを用いたアーバンインテリジェンスの概要と関連アルゴリズム及び実装例。アーバンインテリジェンスは、都市や都市環境におけるデータを収集し、解析して都市の運営やサービスの改善に役立てる技術・概念で、グラフニューラルネットワーク（GNN）を用いたアーバンインテリジェンスでは、都市の複雑な構造や関係性を捉えるために、グラフとして都市をモデル化し、そのモデルを用いて都市の課題や機会を理解し、改善策を提案している。

GNNを用いた製品の特性や機能をモデル化し、市場の反応や需要の変動を予測するサービスの概要

GNNを用いた製品の特性や機能をモデル化し、市場の反応や需要の変動を予測するサービスの概要。Graph Neural Networks (GNN)を用いた製品特性・機能のモデル化と市場の反応・需要変動予測に関するサービスは、以下のような概要となる。

GNNを用いた製造プロセスの各段階をモデル化し、生産ラインの設計や操作の最適化を行うサービスの概要

GNNを用いた製造プロセスの各段階をモデル化し、生産ラインの設計や操作の最適化を行うサービスの概要。Graph Neural Networks (GNN) を用いた製造プロセスの各段階をモデル化し、生産ラインの設計や操作の最適化を行うサービスは、次のような概要となる。

グラフニューラルネットワークを用いた天気予報の概要と関連アルゴリズム及び実装例

グラフニューラルネットワークを用いた天気予報の概要と関連アルゴリズム及び実装例。グラフニューラルネットワーク（GNN）を用いた天気予報は、気象データの複雑な空間的および時間的関係を捉えるための新しいアプローチとなる。従来の天気予報手法は、数値予報モデル（NWP）や統計的手法が主流だが、これらは多くの場合、計算コストが高く、全体の精度向上に限界がある。GNNは、データ間の関係性をグラフとして表現し、その構造を活用して予測精度を向上させることができるため、天気予報への応用が注目されている。

グラフニューラルネットワークを用いた分子シミュレーションの概要と関連アルゴリズム及び実装例

グラフニューラルネットワークを用いた分子シミュレーションの概要と関連アルゴリズム及び実装例。グラフニューラルネットワークを用いた分子シミュレーションは、従来の手法に比べて高い精度や効率性を示すことが期待されたアプローチであり、特に、分子の構造や相互作用の複雑さを捉える能力や、大規模なデータセットからの学習能力が注目されているものとなる。

GNNを用いたIOT技術の概要と関連アルゴリズムおよび実装例

GNNを用いたIOT技術の概要と関連アルゴリズムおよび実装例。IoT技術は、物理的なデバイスがインターネットを通じて接続され、データを交換し合うことを指し、IoTデバイスは、センサーやアクチュエータ、カメラなど、多岐にわたるデバイスから構成されるものとなる。これらのデバイスが生成する膨大なデータを効果的に分析し、予測や最適化を行うことがIoT技術の重要な課題となる。GNNは、ノードとエッジからなるグラフ構造を持つデータを処理するためのニューラルネットワークであり、IoT環境では、以下のような要素をグラフとしてモデル化できる。

GNNを用いた推薦技術の概要と関連アルゴリズムおよび実装例

GNNを用いた推薦技術の概要と関連アルゴリズムおよび実装例。グラフは、グラフ構造データのモデリングと表現における柔軟性と有効性により、広く適用できる表現力豊かで強力なデータ構造であり、生物学、金融、交通、ソーシャル ネットワークなど、さまざまな分野でますます人気が高まっている。レコメンダー システムは、人工知能の最も成功した商用アプリケーションの 1 つであり、ユーザーとアイテムのインタラクションがグラフ構造データに自然に適合することができ、グラフ ニューラル ネットワーク (GNN) の適用においても大きな注目を集めている。ここではGNNを用いたレコメンダー システムについて述べる。

場の理論とコミュニケーション活性化へのAI技術の適用

場の理論とコミュニケーション活性化へのAI技術の適用。人が集まる場所や状況である「場」では、人々はコミュニケーションを通じて意見や感情を共有したり、価値観を交換したりすることができ、これは職場や学校、家庭などの物理的な場所、会議やイベントなどの特定の目的や意識を持った場、あるいはインターネットや”メタバースの歴史と課題及びAIによる支援“でも述べているメタバースなど、仮想的な空間まで含むことができる。「場」とは単なる空間ではなく、そこに集う人々や物、思想、エネルギーが相互作用し、新たな価値や意味を生むための「状況」や「機会」とも言うことができる。

3Dプリンターと生成系AIの組み合わせとGNNの適用

3Dプリンターと生成系AIの組み合わせとGNNの適用。3Dプリンターは、デジタルモデルから三次元物体を作り出すための装置であり、コンピューターで設計された3Dモデルを基に、材料を積層して物体を作り出すものとなる。このプロセスはアディティブ・マニュファクチャリング（積層造形）と呼ばれる。最も一般的な材料はプラスチックだが、金属、セラミック、樹脂、食品、さらには生体材料も使用されている。GNNと生成系AI、そして3Dプリンターの組み合わせによって、複雑な構造や動的な最適化が可能になり、新しい設計・製造プロセスを実現することができる。

その他

エージェントシステムにおけるフレーム問題

エージェントシステムにおけるフレーム問題。エージェントシステムにおけるフレーム問題とは、エージェントが新しい情報を取得する際に、環境の状態や変化を適切に把握し、判断を下すことの難しさを指す。これは具体的には以下のようなケースにあたる。

グラフニューラルネットワークを用いたマルチエージェントシステムの概要と実装例

グラフニューラルネットワークを用いたマルチエージェントシステムの概要と実装例。グラフニューラルネットワーク（GNN）を使用したマルチエージェントシステムは、複数のエージェントがグラフ構造で相互作用し、エージェント間の関係性や依存関係をモデル化する場合に適したアプローチとなる。

数理論理学とGNN

数理論理学とGNN。数理論理学に”グラフニューラルネットワーク“で述べているグラフニューラルネットワーク（GNN）技術を組み合わせることを考える。GNNは、ノード（オブジェクト）とエッジ（関係）から構成されるグラフデータを処理する能力があり、数理論理学の形式的な構造やルールを扱うのに適したアプローチとなっている。この組み合わせにより、論理的推論や知識表現の領域で新たな可能性を提供することが期待されている。

Ontology Based Data Access(ODBA)と生成系AIとGNN

Ontology Based Data Access(ODBA)と生成系AIとGNN。Ontology Based Data Access (OBDA)は、異なる形式や場所に保存されているデータに対して、オントロジーが提供する統一的で概念的なビューを用いてクエリを実行できるようにした手法で、データの意味的な統合と、ユーザーが理解しやすい形式でデータにアクセスできることを目的としたものとなる。

ChebNetの概要とアルゴリズム及び実装例について

ChebNetの概要とアルゴリズム及び実装例について。ChebNet（Chebyshev ネットワーク）は、グラフニューラルネットワーク（Graph Neural Network, GNN）の一種であり、主にグラフ構造データに対する畳み込み操作を実行するための手法の一つとなる。ChebNetは、シグナル処理で使用されるシェビシェフ多項式（Chebyshev polynomials）を利用して、グラフ上での畳み込み演算を近似的に実装している。

PATCHY-SANの概要とアルゴリズムについて

PATCHY-SANの概要とアルゴリズムについて。PATCHY-SANはNiepertにより”Learning Convolutional Neural Networks for Graphs“で提案されたもので、グラフに対する畳み込における問題として近傍グラフが作られるノード列の決定と、近傍グラフの正規化の計算の2つを挙げ、任意のグラフにおいてそれらの問題を解決する手法として提案されたものとなる。この手法では、グラフ同士の類似度を測るのにグラフカーネルであるWeisfeiler-Lehman(WL)カーネルを用いている。具体的なステップとしては、(1)まずWLカーネルで付けたラベルでノードをソートし、グラフから一定数(ω)のノードを選び、それについて距離が近いk個のノードを選んで順序づけして行列を得る、(2)これをノードの属性\(a_v\)ごとに繰り返すことで\(\omega\times k\times a_v\)のテンソルを作り、(3)このテンソルを元に画像と同じ様に畳み込みを行うものとなる。

DCNN(Diffusion-Convolutional Neural Networks)の概要とアルゴリズム及び実装系について

DCNN(Diffusion-Convolutional Neural Networks)の概要とアルゴリズム及び実装系について。DCNNは、画像やグラフなどのデータ構造に対する”CNNの概要とアルゴリズム及び実装例について“でも述べている畳み込みニューラルネットワーク (CNN) の一種で、”グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）の概要とアルゴリズム及び実装例について“で述べているGCNの発展系となる。通常のCNNは、データがグリッド状の構造を持つ場合に効果的だが、グラフや非定型データに対しては直接適用することが難しいという課題があり、GCNは、グラフデータやネットワークデータのような非常に複雑な構造を持つ非格子状のデータに対する深層学習の手法として開発されたものだが、DCNNは、このGCNに対して、”Diffusion Models（拡散モデル）の概要とアルゴリズム及び実装例について“で述べているDiffusion Modelの概念を適用したものとなる。

DeepWalkの概要とアルゴリズム及び実装例について

DeepWalkの概要とアルゴリズム及び実装例について。DeepWalkは、グラフデータ解析のための機械学習アルゴリズムの一つであり、特に、ノードの表現学習（Node Embedding）と呼ばれるタスクに適しており、ノードを低次元のベクトル空間に埋め込むことを目的とした手法で、ノードがグラフ内で隣接するノードと共有する情報をキャプチャし、その情報を使用してノードの埋め込みを学習するものとなる。DeepWalkは、社会的ネットワーク、ウェブページリンクグラフ、協調フィルタリングなど、さまざまなアプリケーションで利用されている。

GraphWaveの概要とアルゴリズム及び実装例について

GraphWaveの概要とアルゴリズム及び実装例について。GraphWaveは、グラフデータの埋め込みを学習するための手法の一つであり、グラフデータ埋め込みは、ノードやエッジの特徴を低次元のベクトルに変換する技術で、グラフデータを機械学習アルゴリズムに適用するために役立つものとなる。GraphWaveは、グラフ構造とその周辺情報を考慮して、効果的な埋め込みを学習することができる特長的なアプローチとなる。

DANMF (Dynamic Attributed Network with Matrix Factorization)の概要と実装例について

DANMF (Dynamic Attributed Network with Matrix Factorization)の概要と実装例について。DANMF（Dynamic Attributed Network with Matrix Factorization）は、動的な属性情報を持つネットワークデータを対象としたグラフ埋め込みの手法の一つであり、ノードの属性情報とネットワーク構造を組み合わせて、ノードの埋め込みを学習するものとなる。この手法は、動的な属性情報が含まれる場合に特に有用で、ノードの属性が時間によって変化する場合や、異なる属性情報が異なる時間ステップで利用可能な場合に適している。

Dynamic Graph Neural Networks（D-GNN）の概要とアルゴリズム及び実装例について

Dynamic Graph Neural Networks（D-GNN）の概要とアルゴリズム及び実装例について。Dynamic Graph Neural Networks（D-GNN）は、動的なグラフデータに対処するために設計されたグラフニューラルネットワーク（Graph Neural Network、GNN）の一種であり、ノードとエッジが時間に応じて変化するようなデータを扱うために設計されたものとなる。(GNNについては”グラフニューラルネットワークの概要と適用事例およびpythonによる実装例について“を参照のこと)このアプローチは、時系列データ、ソーシャルネットワークデータ、交通ネットワークデータ、生物学的ネットワークデータなど、さまざまな領域で用いられている。

Edge-GNNの概要と実装例

Edge-GNNの概要と実装例。Edge-GNN (Edge Graph Neural Network) は、グラフ構造におけるエッジ（辺）に焦点を当てたニューラルネットワークアーキテクチャで、エッジの特徴や重みを活用して、エッジレベルやグラフ全体のタスクを処理することを目的としたものとなる。Edge-GNNは、通常のGNNと異なり、ノード（頂点） ではなく エッジ（辺） に主な焦点を当てたモデルとなる。多くのグラフ解析タスク（例: 関係予測やリンク予測）では、ノード間の接続（エッジ）に関する情報が重要であるため、Edge-GNNは、次のような特性を持つ。

Temporal Graph Neural Networkの概要と実装例

Temporal Graph Neural Networkの概要と実装例。Temporal Graph Neural Networks（TGNN）は、時間情報を考慮したグラフ構造データを処理するためのディープラーニング手法で、静的なグラフニューラルネットワーク（GNN）では時間的な変化を扱えないため、時間依存性や時系列データを活用したグラフ分析が可能になものとなる。TGNNの特徴としては、ノード、エッジ、またはグラフ全体の時間的変化をモデル化し、イベント発生順序や時間依存性の影響を考慮可能なこと、構造が時間とともに変化する動的グラフ（Dynamic Graph）を扱うのに適しており、たとえば、ソーシャルネットワークにおける人々の関係の変化や通信ネットワークのトラフィック変化などを処理可能なことなどがある。

情報統合理論とその応用

情報統合理論とその応用。情報統合理論（Information Integration Theory, IIT）は、心理学者のノーマン・H・アンダーソン（Norman H. Anderson）によって提唱された理論で、人が複数の情報を統合し、意思決定や判断を行うプロセスを理解するために使われるモデルとなる。このモデルは特に認知心理学や社会心理学で重要な役割を果たし、人の判断や評価がどのように形成されるかを表している。

オセロゲームの解法アルゴリズムとGNN

オセロゲームの解法アルゴリズムとGNN。オセロゲーム（Othello）は、2人で対戦するボードゲームで、白と黒のディスクを使ってプレイし、プレイヤーは自分の色のディスクを配置し、相手のディスクを挟んで裏返すことで自分の色に変えるのが基本ルールである競技となる。

GraphRNNの概要とアルゴリズム及び実装例

GraphRNNの概要とアルゴリズム及び実装例。GraphRNNは、グラフ生成に特化したディープラーニングモデルで、特にグラフの構造を学習して新しいグラフを生成する能力に優れたものとなる。このモデルは、ノードとエッジのシーケンスを予測することでグラフ全体を生成している。

参考情報と参考図書

Graph Neural Networkの先端的な研究を行っているGoogleReasearchの”A Gentle Introduction to Graph Neural Networks“、また国内では東工大の村田研のサイトにさまざまなGNNの研究事例が掲載されている。

グラフデータの詳細に関しては”グラフデータ処理アルゴリズムと機械学習/人工知能タスクへの応用“を参照のこと。また、ナレッジグラフに特化した詳細に関しては”知識情報処理技術“も参照のこと。さらに、深層学習全般に関しては”深層学習について“も参照のこと。

参考図書としては”グラフニューラルネットワーク ―PyTorchによる実装―“

“グラフ理論と機械学習“

“Hands-On Graph Neural Networks Using Python: Practical techniques and architectures for building powerful graph and deep learning apps with PyTorch“

“Graph Neural Networks: Foundations, Frontiers, and Applications“等がある。