Structural Deep Network Embedding(SDNE)の概要とアルゴリズム及び実装例

Structural Deep Network Embedding(SDNE)の概要

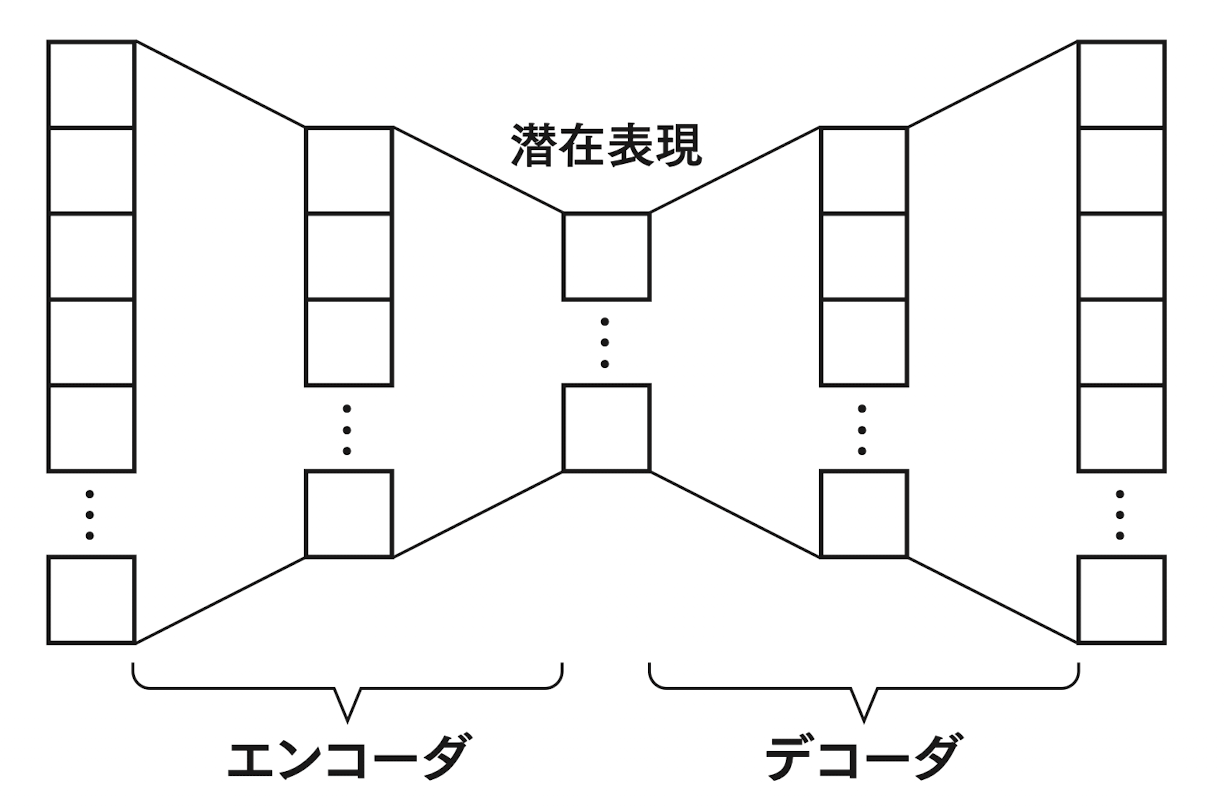
Structural Deep Network Embedding(SDNE)は、オートエンコーダをグラフに拡張したグラフオートエンコーダーの一種となる。

“オートエンコーダー“でも述べているオートエンコーダーは、与えられたデータを潜在空間における低次元ベクトルにエンコードする教師なし学習を行うニューラルネットワークで、具体的な適用例としては”Word2Vec“で述べているWord2Vec等がある。

グラフオートエンコーダーでは、ノードの属性も利用するか、エンコーダーとデコーダーで何を使うか、何を目的関数とするかにより多くのバリエーションがある。

SDNEは、Wangらにより”Structural Deep Network Embedding“で報告されたモデルで、1次の近接性と2次の近接性を同時に維持することを目的とした多層オートエンコーダー(Stacked AutoEncoder)となる。SDNEは、グラフのノード間の構造的な特徴を捉えることに焦点を当てており、隣接ノード間のリンクや、ノードの隣接関係などの情報を保持したまま、低次元の密なベクトル表現に変換することが可能なモデルとなっている。このような低次元の表現を得ることで、大規模なグラフの効率的な処理や、ノード間の類似性や関係性の推定などができるようになる。

SDNEの1次の近接性は以下の様に表される。

\[L_{1st}=\displaystyle\sum_{i,j=1}^n\mathbf{A}_{i,j}||\mathbf{h}_i^{(K)}-\mathbf{h}_j^{(K)}||_2^2\]

ここで\(\mathbf{h}_i^{(K)}\)はノードiの表現の低次元ベクトルで、(K)はK番目の層(Kは隠れ層の数)であることを表している。2次の近接性は以下の式で表される。

\[L_{2nd}=\displaystyle\sum_{i=1}^n||(\hat{\mathbf{x}}_i-\mathbf{x}_i)\odot\mathbf{b}_i||_2^2\]

ここで\(\mathbf{x}_i\)は入力の隣接行列のi行目(ノーiの他ノードへの接続の有無を表すベクトル)、\(\hat{\mathbf{x}}_i\)はオートエンコーダーの出力の行列のi行目、\(\mathbf{b}_i\)は他ノードへの接続の有無の食い違いにペナルティを与えるベクトルで、\(A_{i,j}=0\)ならば、\(b_{i,j}=1\)、\(A_{i,j}=1\)ならば\(b_{i,j}=\beta>1\)(βはハイパーパラメータ)となる。

このようなモデルによりSDNEでは、オートエンコーダー内の中間層で隣接情報を保存するための構造を持ち、近くのノードが低次元空間内でも近くに保たれるように学習される。

これらを使えば、SDNEの目的関数は以下の様に定義される。

\[L=L_{2nd}+\alpha L_{1st}+\lambda L_{reg}\]

ここでαとλはハイパーパラメータ、\(L_{reg}\)は過適合を防ぐためのL2正則化項となる。

\[L_{reg}=\frac{1}{2}\displaystyle\sum_{k=1}^K(||\mathbf{W}^{(K)}||_F^2+||\hat{\mathbf{W}}^{(K)}||_F^2\]

SDNEの損失関数は、再構築誤差と、低次元表現の隣接関係の保存を同時に最小化するように設計され、元のグラフ構造を可能な限り正確に再現しつつ、低次元空間内での隣接関係を保持することができるようになっている。

SDNEのライブラリのサイトは以下のサイトで公開されている。

Structural Deep Network Embedding(SDNE)に関連するアルゴリズム

以下に、SDNEに関連するアルゴリズムについて述べる。

1. DeepWalk:

DeepWalkの概要: DeepWalkは、ランダムウォークとニューラルネットワークを組み合わせた手法で、グラフ構造を低次元ベクトルに変換することを目的としているものとなる。DeepWalkでは、ランダムウォークにより、近くのノードを含むランダムなサブグラフを生成し、これをニューラルネットワークに入力して学習している。DeepWalkの詳細は”DeepWalkの概要とアルゴリズム及び実装例について“を参照のこと。

SDNEとの関連: SDNEは、DeepWalkのようなランダムウォークベースの手法を利用して、グラフの隣接情報を捉えている。ただし、SDNEはオートエンコーダーを用いてより深い学習を行い、より効果的なグラフ埋め込みを実現している。

2. LINE (Large-scale Information Network Embedding): 

LINEの概要: LINEは、大規模な情報ネットワークを効率的に埋め込む手法で、LINEは、1次および2次の隣接関係を同時に最適化することで、グラフ構造を捉えている。LINEの詳細は”LINE（Large-scale Information Network Embedding）の概要とアルゴリズム及び実装例について“を参照のこと。

SDNEとの関連: SDNEもグラフ構造を捉えるために、隣接情報を効果的に利用している。SDNEは、オートエンコーダーを用いて非線形性を取り入れ、より豊かな表現の学習を可能としている。

3. GraREP (Graph Representation learning):

GraREPの概要: GraREPは、グラフ構造の異なる階層的特徴を捉えることを目的とした手法となる。グラフの異なる階層の隣接行列を用いて、低次元のベクトル表現を学習します。GraREPの詳細は”GraREPの概要とアルゴリズム及び実装例“を参照のこと。

SDNEとの関連: SDNEもグラフ構造の特徴を捉えるために、異なる階層の情報を組み込んでいる。SDNEは、オートエンコーダーを用いて異なる階層の情報を効果的に統合し、より精密な埋め込みを学習している。

4. GCN (Graph Convolutional Networks):

GCNの概要: GCNは、グラフデータ上で畳み込みを行うことができるニューラルネットワークの一種となる。GCNでは隣接ノードの情報を利用して、各ノードの表現を更新することで、グラフ埋め込みを行っている。GCNの詳細は”グラフ畳み込みニューラルネットワーク（Graph Convolutional Neural Networks, GCN）の概要とアルゴリズム及び実装例について“を参照のこと。

SDNEとの関連: SDNEもグラフ構造を効果的に捉えるために、隣接情報を考慮している。SDNEは、GCNと同様に、隣接ノードの情報を反映する構造を持っているが、オートエンコーダーによってより高度な特徴表現を学習している。

Structural Deep Network Embedding(SDNE)の適用事例について

以下に、SDNEの適用事例について述べる。

1. ソーシャルネットワーク分析: ソーシャルネットワークでは、ユーザー間の関係やネットワークの構造を理解することが重要であり、SDNEは、ソーシャルネットワークのユーザーやグループの関係性を効果的に捉え、ノードの類似性やコミュニティの特定に役立てられている。

ユーザーのクラスタリング: SDNEによって学習された低次元のベクトル表現を用いて、類似したユーザーをグループ化することができる。

リンク予測: SDNEによって学習されたノードの埋め込みを使用して、新しいノード間のリンクを予測することができる。

2. 推薦システム: 推薦システムでは、ユーザーの行動履歴やアイテムの特徴を元に、個々のユーザーに最適なアイテムを推薦する。SDNEは、ユーザーやアイテムの間の関係性を表現し、効果的な推薦を行うための特徴表現を学習することができる。

アイテムの埋め込み学習: SDNEを使用して、アイテム間の類似性を捉える低次元の埋め込みを学習する。

ユーザーのパーソナライズド推薦: SDNEによって学習されたユーザーの特徴表現を用いて、特定のユーザーに最適なアイテムを推薦する。

3. バイオインフォマティクス: バイオインフォマティクスでは、遺伝子やタンパク質などの生物学的データを解析し、機能や相互作用を理解する。SDNEは、生物学的ネットワークの特徴を抽出し、タンパク質間の相互作用や機能を推定するために利用される。

タンパク質相互作用の予測: SDNEによって学習されたタンパク質の埋め込みを使用して、新しいタンパク質間の相互作用を予測する。

疾患関連遺伝子の特定: 疾患と関連する遺伝子やタンパク質の関係性をSDNEによって学習し、疾患のメカニズムを理解する。

4. インターネット広告のターゲティング:  インターネット広告では、ユーザーの属性や行動を元に、効果的な広告を表示する。SDNEは、ユーザー間の類似性や関連性を学習し、ターゲティングやパーソナライズド広告の向上に役立つ。

ユーザーのセグメンテーション: SDNEによって学習されたユーザーの特徴表現を使用して、類似したセグメントのユーザーグループを特定する。

広告の効果測定: SDNEを用いて広告キャンペーンに参加したユーザーの特徴を分析し、広告の効果を評価する。

SDNEは、グラフ構造を効果的に捉え、低次元の密な表現を学習することで、さまざまなデータ解析や情報推論のタスクに貢献している。

Structural Deep Network Embedding(SDNE)の実装例について

Structural Deep Network Embedding（SDNE）を実装するための例として、Pythonのグラフ処理ライブラリであるNetworkXと、ディープラーニングライブラリのKerasを使用する方法を示す。

1. 必要なライブラリのインストール: まず、以下のライブラリをインストールする。

pip install networkx
pip install keras
pip install tensorflow

2. SDNEの実装: 以下は、SDNEを実装する基本的なステップとなる。

SDNEクラスの定義: まず、SDNEクラスを定義する。このクラスは、ネットワークの学習とベクトル表現の取得を行っている。

import numpy as np
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
import networkx as nx
from sklearn.preprocessing import MinMaxScaler

class SDNE:
    def __init__(self, graph, embedding_size=128, alpha=0.3, beta=0.3, nu1=1e-6, nu2=1e-6, epochs=50):
        self.graph = graph
        self.embedding_size = embedding_size
        self.alpha = alpha
        self.beta = beta
        self.nu1 = nu1
        self.nu2 = nu2
        self.epochs = epochs

    def preprocess_graph(self):
        self.node_num = len(self.graph.nodes())
        self.adj_matrix = nx.adjacency_matrix(self.graph).toarray()
        self.adj_matrix = MinMaxScaler().fit_transform(self.adj_matrix)
        self.adj_matrix = self.adj_matrix + np.eye(self.node_num)

    def create_model(self):
        x = Input(shape=(self.node_num,))
        h = Dense(self.embedding_size, activation='relu')(x)
        y = Dense(self.node_num, activation='sigmoid')(h)

        self.model = Model(inputs=x, outputs=y)
        self.model.compile(optimizer=Adam(lr=0.001),
                           loss='binary_crossentropy')

    def train_model(self):
        self.model.fit(self.adj_matrix, self.adj_matrix,
                       epochs=self.epochs, verbose=1)

    def get_embeddings(self):
        hidden_layer = Model(inputs=self.model.input,
                             outputs=self.model.layers[1].output)
        node_embeddings = hidden_layer.predict(self.adj_matrix)
        return node_embeddings

SDNEの利用例: 次に、実際にSDNEを使用してグラフの埋め込みを取得する例を示す。

# データの読み込みやネットワークの作成
G = nx.karate_club_graph()
sdne = SDNE(G, embedding_size=128, epochs=50)

# ネットワークの前処理
sdne.preprocess_graph()

# モデルの作成
sdne.create_model()

# モデルの学習
sdne.train_model()

# 埋め込みの取得
embeddings = sdne.get_embeddings()
print(embeddings)

この例では、karate_club_graph()関数を使用してカラテクラブのソーシャルネットワークを読み込み、SDNEを適用して128次元のノード埋め込みを取得している。

Structural Deep Network Embedding(SDNE)の課題とその対応策について

以下に、SDNEの主な課題とその対応策について述べる。

1. グラフサイズと計算コスト:

課題:
大規模なグラフに対してSDNEを適用する場合、計算コストが高くなる可能性があり、グラフのノード数やエッジ数が増えると、モデルの学習や埋め込みの計算に要する時間が増加する。

対応策:
ミニバッチ学習:“ミニバッチ学習の概要とアルゴリズム及び実装例“でも述べているミニバッチ学習を導入して、大規模グラフでも効率的に学習を行う。
分散学習: 複数の計算ノードを使用して学習を並列化し、計算速度を向上させる。
グラフサンプリング: グラフの一部をサンプリングして学習することで、全体のグラフを扱うより効率的になる。

2. 非線形性と過学習:

課題:
SDNEは、オートエンコーダーを用いて非線形な特徴表現を学習するが、過学習のリスクがある。特に、高次元のデータや複雑なグラフ構造では、過学習が発生しやすくなる。

対応策:
ドロップアウト: ドロップアウトを使用して、過学習を抑制する。
正則化: L1正則化やL2正則化を導入して、モデルの複雑さを制御する。
早期停止: 検証データの損失が改善しなくなった時点で学習を停止し、過学習を防ぐ。

3. グラフの特徴の抽出と表現学習:

課題:
SDNEは、グラフの局所的な隣接関係や構造を捉えることができるが、グラフの全体的なパターンや特徴を効果的に表現することが難しい場合がある。

対応策:
多層構造: より深いネットワークアーキテクチャを使用して、より複雑な特徴を抽出する。
グラフの専門知識の利用: グラフのドメイン特性を活用して、より効果的な特徴表現を設計する。
多様な損失関数: グラフの異なる特性に適した損失関数を導入して、学習を最適化する。

4. ノードの次元削減と情報の損失:

課題:
SDNEは、高次元のノード特徴を低次元の埋め込みに圧縮するため、情報の損失が発生する。低次元埋め込みでは、元のグラフ構造や特徴の一部が失われることがある。

対応策:
適切な埋め込み次元の選択: 埋め込み次元を適切に調整し、情報の損失を最小限に抑える。
潜在的な特徴の解釈: 低次元埋め込みの潜在的な特徴を解釈し、失われた情報を補完する。
多次元埋め込み: 複数の異なる次元で埋め込みを学習し、情報の多様性を確保する。

5. ノイズや不完全なデータへの対処:

課題:
グラフデータには、ノイズや欠損などの不完全さが含まれる場合があり、SDNEは、これらの不完全なデータに対してロバストな学習を行う必要がある。

対応策:
データの補完: 欠損データを補完する手法を導入して、不完全なデータに対処する。
ノイズ除去: ノイズを除去するためのフィルタリングや、ノイズにロバストな損失関数を利用する。
アンサンブル学習: 複数のSDNEモデルを組み合わせて、ロバストな埋め込みを得る。

参考情報と参考図書

グラフデータの詳細に関しては”グラフデータ処理アルゴリズムと機械学習/人工知能タスクへの応用“を参照のこと。また、ナレッジグラフに特化した詳細に関しては”知識情報処理技術“も参照のこと。さらに、深層学習全般に関しては”深層学習について“も参照のこと。

参考図書としては”グラフニューラルネットワーク ―PyTorchによる実装―“

“グラフ理論と機械学習“

“Hands-On Graph Neural Networks Using Python: Practical techniques and architectures for building powerful graph and deep learning apps with PyTorch“

“Graph Neural Networks: Foundations, Frontiers, and Applications“等がある。