ガウス的世界
“機械学習における確率的アプローチ“でも述べている機械学習の確率的アプローチでは、ガウス分布から出発した様々な確率分布を用いて計算が行われている。
このガウス分布(正規分布)は、カール・フリードリヒ・ガウス(Carl Friedrich Gauss) にちなんで名付けられたものだが、実は以下のように「最初に発見した」のはガウスではないと言われている。
| 年代 | 学者名 | 貢献内容 |
|---|---|---|
| 1733年 | エイブラハム・ド・モアブル(Abraham de Moivre) | 最初に正規分布の形を近似的に発見(二項分布の極限として) |
| 1809年 | カール・フリードリヒ・ガウス(Carl F. Gauss) | 天体観測の誤差モデルとして正規分布を明示的に使用・導入 |
| 1810年 | ピエール=シモン・ラプラス(Pierre-Simon Laplace) | 中心極限定理の初期形(誤差が正規分布に近づく)を数学的に発展 |
では、どうして「ガウス分布」と呼ばれるようになったのかというと、上記の表にあるよあにガウスは観測データの誤差を数理的に分析し、正規分布が自然であることを示し、1809年の著書「天体運動論(Theoria motus corporum coelestium)」で、最尤法(最もありそうな値を推定する方法)と正規分布 を組み合わせて、天体の軌道決定に応用し、「ガウス分布(Gaussian distribution)」と呼ばれるようになったと言われている。
ガウス分布は以下の式で表される。
\[f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]
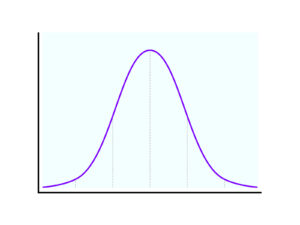
これをグラフで書くと以下のような形となり

平均を中心に山型となり、中心から距離が離れるほど指数的に急激に減る形を示す。
このガウス分布に対して、上表のようにラプラスは中心極限定理(Central Limit Theorem)を用いて、たくさんの小さなランダム要素(誤差や揺らぎ)が合わさると、その結果は正規分布に近づく、という事を証明している。
これは、例えば、たくさんの人がコインを10回投げ、表が出る回数は、人によってバラバラとなるが、その「表の出る回数の分布」をグラフにすると、真ん中に山がある釣鐘型(=ガウス分布)になるという事を言っており、その他にも以下のような自然界の様々な事象であらわれる現象となっている。
| 現象 | ガウス分布になる理由 |
|---|---|
| 人の身長 | 遺伝、栄養、環境、成長ホルモンなど多数の要因が積み重なる |
| 計測誤差 | 測定器の精度、温度、操作者の手ブレなどの誤差の合成 |
| ノイズ(音、電波) | 多くの微小なランダム信号の合成によるもの |
| 天体の観測値 | 大気揺らぎや観測誤差が合成されている |
この法則の意味するところは、たとえ1つ1つの要因がバラバラで不規則でも、それが多数集まると「平均」に従い、全体が秩序だった形(釣鐘型)になるということであり、偶然の集まりが、秩序ある形(法則)を生むという法則であると言い換えることができる。
これは、個々の事象は偶然的(確率的)であっても、全体のふるまいは確定的(決定論的)に見えるという、確率論と決定論の橋渡しを行なっているとも言うことができる。これは「ミクロなランダム性が、マクロな規則性を生む」という自然の不思議を表している。
このことは、アイシュタインの有名な言葉である“God does not play dice with the universe.”(神はサイコロを振らない)”という名言に対して、ガウス分布は「神がサイコロを振ったとしても、その結果が美しい秩序になる」ことを数学的に示しているという呵責ができることを示している。
このガウス分布は、自然現象だけでなく、情報科学の世界にも現れ、「最大エントロピー原理」と呼ばれる原理にも当てはめられる。これは、平均と分散だけが決まっているときに、最も情報量が少ない(最も無知を表す)分布がガウス分布であり、「我々が偏見なくものごとを仮定(最も何も知らない状態)すると、ガウス分布になる」と言い換えることができる。
このガウス分布の、情報・エネルギー・観測の不確実性の根源的な構造であるという特徴を生かし、AIや機械学習では以下のような応用が考えられてきた。
- ガウス過程 → 不確実性を関数として捉える
- ベイズ推論 → ガウス分布は計算が美しく収束する“便利で自然”な分布
- 生成モデル(例:VAE)では、潜在空間をガウス分布に置くことで滑らかな生成が可能になる
非ガウス的世界
ただし、このガウス分布が成り立つには「互いに独立であること」や「分散が有限であること」といった数学的条件が必須となる。
「互いに独立であること」とは、数学的には以下のように表され
\[P(X=x\ and\ Y=y)=P(X=x)\cdot P(Y=y)\]
一方の出来事が起こっても、もう一方の確率には何の影響もないということを示し、これを哲学的な言葉で意言い換えると、「因果関係が存在しない」か、「情報的に無関係」な存在であるということができる。
これは、世界は、複数の要素がバラバラに起こっているように見え、「偶然の一致」だけで成り立っているという「原子的世界観」(古代ギリシャのデモクリトスのような)に近いものだということができる。
また、情報理論的な観点でいうと、AとBが独立だと仮定するというのは、「Aの情報を知っても、Bには何も言えない」という無知の宣言であり、現実には関係があるかもしれないけど、観測できない・制御できないので、独立とみなすという「合理的なモデリングの最小単位」という視点を表している。
もう一つの前提条件である「分散が有限であること」とは数学的には以下の式が有限であることを示す。
\[Var(x)=E|(X-x)^2|\]
これは、哲学的な言葉でいうと「世界の揺らぎには限度がある」という信念であり、分散が有限というのは、「異常値(outlier)も起こるが、常識の範囲内」という「秩序ある自然観・常識的宇宙観」に基づいているということができる。
これは、別の観点から見ると、「分散が無限だと測定不能だから有限とする」、「人間が扱える世界だけを世界とする」という科学的実用主義の観点に沿っているということもできる。この視点は、統計的には、「サンプルをたくさん集めれば平均に収束する」という大数の法則ともつながり、「世界は繰り返せば安定的に把握できる」という、経験と蓄積に基づく世界観になる。
これらの条件は以下のような世界の設計図を前提としているということができる。
- 世界は本質的に秩序立っているが、その秩序は確率的にしか見えない
- 我々は完全な知識を持たないが、制約ある中で最も合理的なモデルを使う
- 観測可能な世界だけを前提に、シンプルな法則で現象を記述しようとしている
この前提条件に対して、現実の世界はある出来事や構造が、別の出来事と“関係している”世界でもあり、現実の多くの現象は因果構造を持っている。
これらはネットワーク構造として表され、それらのネットワーク上で、情報・感情・感染・影響力などが伝播し、この世界は「独立な点の集合」ではなく、「相互に影響しあう構造体」であるということができる。これらをモデルとして扱うには、ガウス分布等の確率分布をベースとしたモデルでは不適切であり、”グラフニューラルネットワーク“で述べているようなグラフ構造を解析するものが必要となってくる。
また、極端な出来事が頻繁に起こる世界では、分散すら定義できないことも度々生じる。これは数学的にはパレート分布(冪分布)と呼ばれている分布で表され、現実世界の例では富の分布(上位1%が全体の40%)であったり、SNSのバズ(1つの投稿が100万回拡散)、地震の大きさ(多数の小地震、稀に巨大地震)に表され、9.11テロ、リーマンショック、コロナパンデミックのように「過去のデータでは予測できなかったが、極端な影響をもたらす出来事」と認織されるものが存在している。
このこれらは分散すら測れない領域の事象は、ブラックスワン(N.タレブ)と呼ばれ、これを数理的にモデル化するには、従来のガウス的世界観を超えるアプローチが必要となってくる。
このブラックスワン的現象のモデル化には、主に以下のアプローチが使われている。
| モデルアプローチ | 概要 | キーワード |
|---|---|---|
| パレート分布・冪分布(重尾分布) | 「まれだけど大きい」事象を統計的に考慮 | スケールフリー・α安定分布 |
| 極値理論(Extreme Value Theory) | 最大値や最小値の挙動だけを扱う統計理論 | GEV分布・GPD分布 |
| Lévy過程(ジャンプ過程) | 飛び跳ねるランダム変化 | 不連続・重尾分布 |
| カオス理論・複雑系 | 微小な初期差が巨大な変化を生む動力学系 | 初期条件鋭敏性・ストレンジアトラクター |
| エージェントベースモデル(ABM) | 個体相互作用から突発的なマクロ現象が生まれる | 相転移・クリティカルポイント |
| ブラックボックスモデル(AI/LLM) | 原因を明示せず、大量データから予兆や兆候を捉える | 異常検知・生成モデル |
これらに対するAI的なアプローチとしては、”人工生命とエージェント技術“で述べているエージェントベースモデル(ABM)で個々のエージェントを単純なルールで動かし、その相互作用から、突発的に全体構造が変化を検出したり、”機械学習による自動生成“で述べている生成系モデルを用いたブラックボックス的アプローチにより、ブラックスワンを「理論的に説明」するのではなく、「経験的に検出・予測」しようとすることが近年検討されている。これは、モデル全体を把握するのでなく、兆候をつかむ」視点への転換するということができる。
人類の歴史は、「例外」とされた出来事によって形作られてきており、従来の科学は「予測可能な範囲で、繰り返し可能なもの」をモデル化しようとしてきたものに対して、予測不可能で一度きりのものを予測しようとする新たなアプローチであるということができる。
モデル化とは、「理解できないものに、知的な輪郭を与えようとする行為」であり、そこには様々な観点があるということができる。
参考図書
以下に、今回の考察に深く関連参考文献について述べる。
【A. ガウス分布・確率論・中心極限定理に関する基礎と哲学】
| 書名 | 著者 | 内容 |
|---|---|---|
| 『Foundations of the Theory of Probability: Second English Edition』 | アンドレイ・コルモゴロフ | 現代確率論の形式的基礎。独立性・分散の厳密な定義が中心。 |
| 『Introduction to Probability and Statistics』 | ||
| 『ランダムネスの哲学』 |
【B. 非独立な世界・ネットワーク・因果モデル】
| 書名 | 著者 | 内容 |
|---|---|---|
| 『The Book of Why(なぜ?の本)』 | ジューディア・パール | 因果推論の父による、因果グラフとベイズネットの思想的意義。非独立性=因果性の核心。 |
| 『ネットワーク科学』 | アルバート=ラズロ・バラバシ | スケールフリー・リンク構造・パレート則・影響の伝播について体系的に解説。 |
| 『複雑系とはなにか』 |
【C. 分散無限な世界・極値理論・ブラックスワン現象】
| 書名 | 著者 | 内容 |
|---|---|---|
| 『ブラック・スワン 不確実性とリスクの本質』 | ナシーム・ニコラス・タレブ | 分散無限の世界観、パレート分布、リスク管理の限界を哲学・実例の両面から展開。 |
| 『Introduction to Extreme Value Theory: Applications to Risk Analysis and Management』 | ||
| 『禁断の市場 フラクタルでみるリスクとリターン』 | ベヌワ・マンデルブロ | 冪乗則、フラクタル幾何学、自然界の不連続性へのアプローチ。 |
【D. AI・機械学習・ブラックスワン検出への応用】
| 書名 | 著者 | 内容 |
|---|---|---|
| 『パターン認識と機械学習』 | クリストファー・M・ビショップ | ベイズ推論とガウス分布の数学的背景、ガウス過程などAI的確率アプローチの核。 |
| 『Deep Learning』 | Ian Goodfellow 他 | VAE・GANなど生成モデルを含めたAIの生成・予測的アプローチ。 |
| 『異常検知と機械学習』 | 井出剛 | ブラックスワンの予兆検出に不可欠な異常検知アルゴリズムの体系的紹介。 |
| 『人工知能と人工生命の基礎』 | 伊庭斉志 | 人工生命技術の基礎。 |

コメント
[…] ガウス的世界と非ガウス的な世界のモデリング。”機械学習における確率的アプローチ“でも述べている機械学習の確率的アプローチでは、ガウス分布から出発した様々な確率分布を用いて計算が行われている。このガウス分布(正規分布)は、カール・フリードリヒ・ガウス(Carl Friedrich Gauss) にちなんで名付けられたものだが、実は以下のように「最初に発見した」のはガウスではないと言われている。 […]