機械学習技術 人工知能技術 デジタルトランスフォーメーション技術 確率的生成モデル 本ブログのナビ 深層学習技術 ノンパラメトリックベイズとガウス過程 サポートベクトルマシン Clojureと関数プログラミング
Clojureを用いた確率的プログラミング(Probabilistic Programming)
以前ベイズモデル等の確率的生成モデルで述べたStanやBUSGS等は、確率的プログラミング(Probabilistic Programming:PP)とも呼ばれる。PPは確率モデルを何らかの形で指定し、それらのモデルの推論が自動的に実行されるプログラミングパラダイムとなる。それらの目的は確率モデリングと汎用プログラミングを統合して、株価の予測、映画の推奨、コンピュータの診断、サイバー侵入の検出、画像検出など、さまざまな不確実な情報に対して、様々なAI技術と組み合わせたシステムを構築することにある。
確率的プログラミングに使用されるプログラミング言語は、確率的プログラミング言語(Probabilistic Programming Language:PPL)と呼ばれ、Rで実装されるStan、BUGS、JuliaのライブラリであるPicture、Turing、Gen、pythonのライブラリであるPyStan、PyMC、pomegranater、Lea、bayesloop、TensorFlowのライブラリとしてのEdward、Tensorflow Probability、PyTorchのPyro、JavaのBLOG、PrologのDyna、ProbLog、SchemaのChurch、ClojureでのAnglican、Distributions等多種多様なものが提案されている。
参考情報としては「The Design and Implementation of Probabilistic Programming Languages」、「Towards common-sense reasoning via conditional simulation: legacies of Turing in Artificial Intelligence」、「Practical Probabilistic Programming」「Probabilistic-Programming.org」等がある。
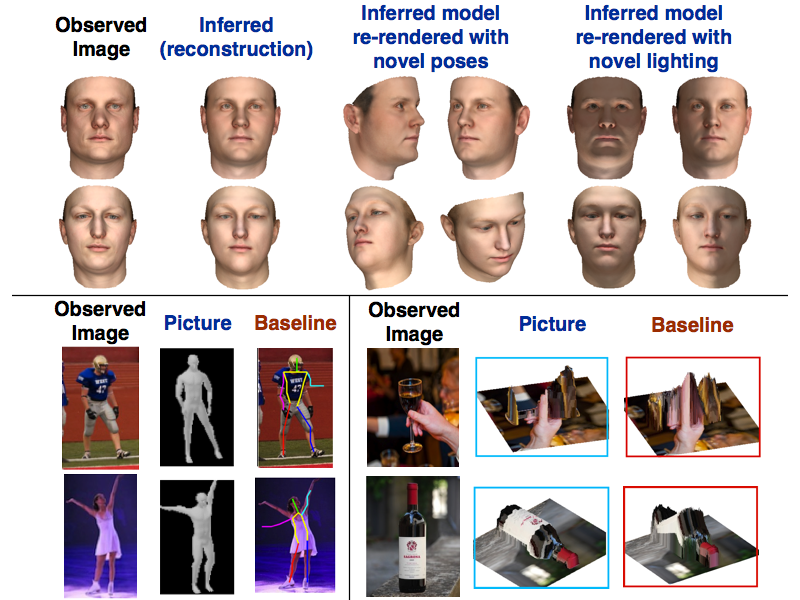
最近の研究例で言うと、前述のJuliaのPictureによる確率的生成モデルを用いた2D画像からの3D画像裏生成や、特徴データの抽出。

強化学習への適用

メタ推論への適用

制約確率的シミュレーションへの適用。

等様々な分野で確率的プログラミングが応用されている。
今回は、この確率的プログラミングへのClojureでのアプローチについて述べる。ClojureでのアプローチではAnglican、Distributions等あるが、今回はSchemaのChurchをベースに検討されたAnglicanについて述べる。
Anglicanは公式HPでは以下のように定義されている。「Anglicanは、 Clojureおよび ClojureScriptと統合された確率的プログラミング言語です。
Anglican には洗練された理論的背景が組み込まれており、探索するように招待されていますが、その価値命題は、確率的環境で直感的なモデリングを可能にすることです。これは学術的な演習ではありませんが、確率論的推論を効果的にする実用的な日常の機械学習ツールです。
ユーザーまたはリモート システムと対話しますか? そして、彼らが予期せぬ行動をするという不幸な経験をすることがよくあります。数学的に言えば、非決定論的または確率論的な振る舞いを観察します。Anglican を使用すると、このすべての確率論をキャプチャする確率変数を表現でき、データから学習して Clojure プログラムで情報に基づいた意思決定を実行できるようになります。」
詳細は公式HP及び論文「A New Approach to Probabilistic Programming Inference」を参照のこと。
以下、具体的な実装の説明にはいる。まず、評価のPFとしてGorilla Replの導入を行う。

Gorilla ReplはPythonのJupyter notbookに相当するwebベースの開発環境となる(最近はJupyterを直接利用できるようだがそちらの説明は割愛する)。Grilla Replを利用するには、まず専用のプロジェクトを作成する。
> lein new app gr-test(任意のプロジェクト名)これまで用いてきたシンプルなプロジェクトのテンプレート作成ではなく、アプリケーションプロジェクトのテンプレートであることに注意が必要となる。後は、上記で作成したプロジェクトのproject.cljファイルにGrilla Replのプラグインを記述する。
(defproject gr-test "0.1.0-SNAPSHOT"
:description "FIXME: write description"
:url "http://example.com/FIXME"
:license {:name "EPL-2.0 OR GPL-2.0-or-later WITH Classpath-exception-2.0"
:url "https://www.eclipse.org/legal/epl-2.0/"}
:dependencies [[org.clojure/clojure "1.11.1"]]
:main ^:skip-aot gr-test.core
:target-path "target/%s"
:plugins [[org.clojars.benfb/lein-gorilla "0.6.0"]]
:profiles {:uberjar {:aot :all
:jvm-opts ["-Dclojure.compiler.direct-linking=true"]}})公式HPでは”[lein-gorilla “0.4.0”]を入れろとあるが、それを入れると動作しない。代わりに上記のように[org.clojars.benfb/lein-gorilla “0.6.0”]を入れることに注意が必要となる。
プロジェクトのディレクトリのトップから、ターミナルで”lein gorilla”と入力すると以下のようにgorilla-replが立ち上がる。
>lein gorilla
………………………………………
Gorilla-REPL: 0.6.0
Unable to reach update server.
Started nREPL server on port 49989
Running at http://127.0.0.1:49991/worksheet.html .
Ctrl+C to exit.任意のブラウザで「http://127.0.0.1:49991(server立ち上げごとにアドレスは変わる)/worksheet.html」にアクセスすると、上記のようなweb REPL環境がたちがる。コマンドHELPは「CTRL」+g(素早く2回)で表示されるが、基本的には、Jupyterと同様に、コードを書き込み「shift」+「enter」で評価できる。
次にanglicanの利用について述べる。anglicanのexampleはgitのproblog/anglican exampleからファイルをダウンロードし、その中のworkshhetsファイルを先ほど作成したプロジェクトフォルダ(gr-test)にコピーして、gorilla REPLで「CTRL」+g(素早く2回)で「Load a worksheet」を選ぶことで利用することができる。
まず必要なライブラリを先ほど作成したプロジェクト(gr-test)のproject.cljファイル内に設定する。
(defproject gr-anglican "0.1.0-SNAPSHOT"
:description "FIXME: write description"
:url "http://example.com/FIXME"
:license {:name "EPL-2.0 OR GPL-2.0-or-later WITH Classpath-exception-2.0"
:url "https://www.eclipse.org/legal/epl-2.0/"}
:dependencies [[org.clojure/clojure "1.11.1"]
[anglican "1.1.0"]
[net.mikera/core.matrix "0.62.0"]]
:main ^:skip-aot gr-anglican.core
:target-path "target/%s"
:plugins [[org.clojars.benfb/lein-gorilla "0.6.0"]]
:profiles {:uberjar {:aot :all
:jvm-opts ["-Dclojure.compiler.direct-linking=true"]}})ここで以下の式をベースとした分類問題について考える。
\[p(x,c|\theta)=p(x|c,\theta)p(c|\theta)=N(x|\mu_c,\Sigma_c)\pi_c\]
c∈0,…,Cは分類のクラスであり、x∈ℝDは特徴量の集合、θは分類のパラメータ集合となり、それらは事前確率πと、平均μc、分散Σcからなる。各データ点の分類が既知である場合(つまり,データセットがある場合),一般に分類タスクと呼ばれ,このモデルを分類モデルと呼ぶことができる.このモデルは多クラスガウス判別分析(GDA)と呼ばれる。もし、各データ点の正しい分類がわからず、観測された特徴量のリストだけがある場合このモデルはガウス混合モデル(GMM)と呼ばれる。
ここでは、ラベルが指定されたデータ点 と、ラベルが特定されていないデータ点の両方を考慮できるアプローチについて考える。
まずAnglicanのlog-sum-exp関数を使って以下のようなGDA関数を定義する。
(defdist gda [pi feature-dists]
[class-dist (discrete pi)
C (count pi)]
(sample* [this]
(let [my-class (sample* class-dist)
my-features (sample* (nth feature-dists my-class))]
[my-class my-features]))
(observe* [this [my-features my-class]]
(if (not (nil? my-class))
(+
(observe* class-dist my-class)
(observe* (nth feature-dists my-class) my-features))
(reduce log-sum-exp
(map
#(+'
(observe* class-dist %)
(observe* (nth feature-dists %) my-features))
(range C))))))以下の関数は、上記のモデルを用いて個々のデータ点を分類するための関数となる。classification-log-probabilities関数 は,GDA インスタンスと,特定の特徴量の集合を受け取り,この特徴量のクラスごとの集合を正規化しない対数確率のリストとして返す。classification-probabilities関数は、上記の関数を呼び出し、その結果を指数化して正規化し、正規確率を返す。
分類に対する分布ではなく,予測された分類結果が必要な場合は,classify-feature関数を用いる。これは、各分類の尤もらしさを対数確率を使って計算し,index-of-maximum関数を使って,それらの中で最も確率の高い分類を単純に返すものとなる。
(defn classification-log-probabilities [gda-dist feature]
(map
(fn [c] (observe* gda-dist [feature c]))
(range (:C gda-dist))))
(defn classification-probabilities [gda-dist feature]
(let [unnormalized (classification-log-probabilities gda-dist feature)
sum (reduce log-sum-exp unnormalized)
normalized (map #(- % sum) unnormalized)]
(map #(Math/exp %) normalized)))
(defn index-of-maximum [lst]
(second
(apply max-key first
(map
(fn [x y] [x y])
lst
(range)))))
(defn classify-feature [gda-dist feature]
(let [unnormalized (classification-log-probabilities gda-dist feature)]
(index-of-maximum unnormalized)))以下の簡単な例で上記を確認する。上記のGDA分布とヘルパー関数を用いて、指定された特徴分布と事前分類確率を持つGDA分布を作成する方法を示している。そして,そのGDAを用いて,特徴量セットを分類し,それぞれの分類の確率を計算している。
(def feature-dist-1 (mvn [0 0] [[4 3] [3 4]]))
(def feature-dist-2 (mvn [0 10] [[10 -3] [-3 5]]))
(def feature-dist-3 (mvn [10 10] [[6 0] [0 8]]))
(def pi [1 1 1])
(def my-gda (gda pi (list feature-dist-1 feature-dist-2 feature-dist-3))) ;;training data
(def x [5 5]) ;; test data
(def probs (map #(Math/round (* 100 %)) (classification-probabilities my-gda x)))
(plot/bar-chart '(0 1 2) probs)
(reduce str (map #(str (Math/round (* 100 %)) "% ") (classification-probabilities my-gda x)))
;; "43% 41% 15% "
(str "The feature " x " has classification " (classify-feature my-gda x))
;;The feature [5 5] has classification 0"
上記は、正しい分類確率piと各分類に対する正しい特徴分布がわかっている場合にのみ機能する。以下のコードでは、これらのパラメータに事前分布を置き、与えられたデータからそれらを推測し、データ点xの分類の事後予測値を出力することを行う。
;; HYPERPARAMETERS (for priors):
(def nu [1 1 1])
(def alpha [1 1])
;; PRIORS:
(def mu-priors (mvn nu (mat/identity-matrix 3)))
(def sigma (mat/identity-matrix 3))
(def pi-prior (dirichlet alpha))
(defquery gda-trainer [data x]
(declare :primitive mat/zero-matrix mat/to-vector mat/identity-matrix gda classification-probabilities)
(let [N (count data)
;; sample parameters
mu1 (sample mu-priors)
mu2 (sample mu-priors)
pi (sample pi-prior)
;; construct GDA distribution
feature-dists (list (mvn mu1 sigma) (mvn mu2 sigma))
gda-dist (gda pi feature-dists)]
;; condition on data
(loop [n 0]
(if (< n N)
(do
(observe gda-dist (nth data n))
(recur (+ n 1)))))
;; now project the type of x
(classification-probabilities gda-dist x)))例として、以下のデータからGDA分布のパラメータを推論する。このデータでは、いくつかの特徴は分類が既知であることに注意が必要となる。しかし、分類が不明な特徴もあるので、パラメータを学習するためには、確率的プログラムは全ての可能な分類について和をとる必要がある。特に、タイプ0であることが分かっている分類がないことに注意が必要である。
このデータが与えられたとき、我々は特徴セットxの事後的な分類を近似することを行う。
(def dataset [
[[3 3 3] 1]
[[1 1 1]]
[[0 0 0]]
[[5 5 5] 1]
[[4 4 4] 1]
[[-1 -1 -1]]
[[-2 0 0]]
])
(def x [1.5 1 1])実際にこの種の分類問題のパラメータを学習することは,かなり複雑な推論問題となる。ここでは、AnglicanのIPMCMC推論アルゴリズムと、10万回のシミュレーションを用いて、真の事後分布を近似的に求める。
(def S 100000)
(def particles 100)
(def nodes 10)
(def samples (take S (drop S
(doquery :ipmcmc gda-trainer [dataset x]
:number-of-particles particles :number-of-nodes nodes))))
(def weights (map :log-weight samples))
(def projections (map :result samples))
(take-last 10 projections)
;;((0.538848314823797 0.46115168517620253) (0.538848314823797 0.46115168517620253)
(0.538848314823797 0.46115168517620253) (0.538848314823797 0.46115168517620253)
(0.538848314823797 0.46115168517620253) (0.9837451961913958 0.016254803808604182)
(0.9837451961913958 0.016254803808604182) (0.9837451961913958 0.016254803808604182)
(0.9837451961913958 0.016254803808604182) (0.9837451961913958 0.016254803808604182))最終的な結果は以下のようにまとめられる。
(defn calculate-mean [series]
(empirical-mean
(partition 2
(interleave series weights))))
;; this will work better
(def percentages (map #(Math/round (* 100 %)) (calculate-mean projections)))
(plot/bar-chart (range (count percentages)) percentages)
(reduce str (map #(str % "% ") percentages))
;;"89% 11%"
データ点Xは分類1ではなく、分類0であることが89%の尤度で得られている。

コメント
[…] Clojureを用いた確率的プログラミング(Probabilistic Programming) […]
[…] 次に、以前述べたanglicanを使ったHMMについて述べる、環境設定等は”Clojureを用いた確率的プログラミング“を参照のこと。前述と同様にprojectファィルを作り、project.cljファイルに […]
[…] 確率的プログラミング: “Clojureを用いた確率的プログラミング(Probabilistic Programming)“でも述べている確率的プログラミングは、確率モデルを記述するための高水準のプログラミング言語を使用してモデルを定義し、モデルの事後分布を推定する手法となる。”マルコフ連鎖モンテカルロ(MCMC)モデルのStanを使ったRとClojureによる解析“にも述べているStanやPyroなどのライブラリが確率的プログラミングのために利用される。 […]