PATCHY-SANの概要
“グラフ畳み込みニューラルネットワーク(Graph Convolutional Neural Networks, GCN)の概要とアルゴリズム及び実装例について“や、”ChebNetの概要とアルゴリズム及び実装例について“で述べられているSpectralなグラフ畳み込みでは以下の様な課題があった。
- 隣接行列から固有値を計算したりグラフ全体を扱うため、グラフが大きくなると計算量が爆発する
- Spectralなグラフ畳み込みはグラフ構造が固定である前提があり異なるグラフへの一般化が困難で、学習したフィルタは、他の構造には適用できない。
- 有向グラフのグラフラプラシアンの定義が定まっていないため、Spectralなグラフ畳み込みは無向グラフしか扱えない。グラフに対する変動があると、基底である固有ベクトルに変動を及ぼす。
Spectralなグラフ畳み込みは、グラフ信号処理立場であり、それらを改善するため、ノードの表現を学習する際に、その周囲のノードの表現を利用して更新することでグラフ構造を反映したSpatialなグラフ畳み込みが検討されている。
今回は、そのSpacialなグラフ畳み込みの一つであるPATCHY-SANについて述べる。
PATCHY-SANはNiepertにより”Learning Convolutional Neural Networks for Graphs“で提案されたもので、グラフに対する畳み込における問題として近傍グラフが作られるノード列の決定と、近傍グラフの正規化の計算の2つを挙げ、任意のグラフにおいてそれらの問題を解決する手法として提案されたものとなる。
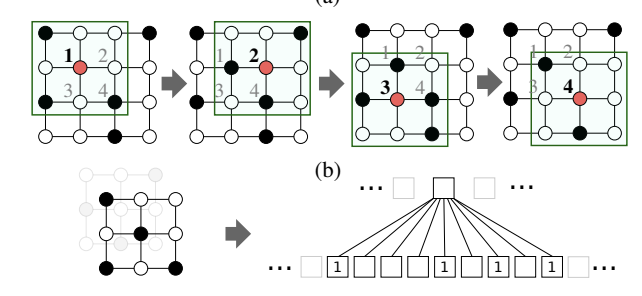
この手法では、グラフ同士の類似度を測るのにグラフカーネルであるWeisfeiler-Lehman(WL)カーネルを用いている。具体的なステップとしては、(1)まずWLカーネルで付けたラベルでノードをソートし、グラフから一定数(ω)のノードを選び、それについて距離が近いk個のノードを選んで順序づけして行列を得る、(2)これをノードの属性\(a_v\)ごとに繰り返すことで\(\omega\times k\times a_v\)のテンソルを作り、(3)このテンソルを元に画像と同じ様に畳み込みを行うものとなる。

このアプローチにより、PATCHT-SANは以下の3つの特徴を持つ。
- 計算量がノード数に対してほぼ線形であり大規模グラフに対して適用可能。

上記の表は、PATCHT-SANと従来のGCNとの処理時間を示したものとなる。従来の手法では、グラフの規模が大きくなるにつれ、処理時間が増大していくが、PATCHT-SANでは処理時間が大幅に低減されている。
- 学習した特徴の可視化の機能を有し、それによってグラフの構造を見出すことができる。

上記の図は、制限付きボルツマン・マシン(RBM)での可視化の結果となる。トーラス(左上)、a preferential attachment graph(左下)、 a co-purchasing network of political books(右上)、a random graph(右下)に対する約100ノードのこれらのグラフのインスタンスが左側にそれぞれ描かれている。また、特徴量の重みの視覚的表現(ピクセルの色が濃いほど、対応する重みが強い)と、RBMから特徴量に対応する隠れノード以外を設定してサンプリングした3つのグラフが示されている。ここでの黄色のノードは、隣接行列の位置が1のものとなる。
- 特徴量の人手による作り込みをすることなく、対象領域に依存した特徴を学習することができる。
PATCHY-SANのアルゴリズム
PATCHY-SANの基本的なアルゴリズムを以下に示す。(“Learning Convolutional Neural Networks for Graphs“より抜粋)
1. Select Node Sequence:
ノード列の選択とは、各入力グラフに対して、受容体配列の選択となる。アルゴリズム1はそのような手順の一つである。
まず、入力グラフの頂点が、与えられたグラフラベルに関してソートされる。次に、得られたノード列を与えられたストライドsで走査し、訪問した各ノードに対して、アルゴリズムが実行され、ちょうどw個の受容野が作成されるまで、受容野が構築されるものとなる。
1: input: graph labeling procedure `, graph G = (V, E), stride
s, width w, receptive field size k
2: Vsort = top w elements of V according to `
3: i = 1, j = 1
4: while j < w do
5: if i ≤ |Vsort| then
6: f = RECEPTIVEFIELD(Vsort[i])
7: else
8: f = ZERORECEPTIVEFIELD()
9: apply f to each input channel
10: i = i + s, j = j + 12. Neighborhood Assembly:
前のステップで識別された各ノードについて、受容野を構築するため、入力ノードの局所近傍領域を構築する。近傍領域のノードは受容野の候補となる。近傍探索のステップは、入力としてノードvと受容野のサイズkが与えられると、この手続きは幅優先探索を実行し、vからの距離が大きくなる頂点を探索し、集められたノードの数がkより小さい場合、Nに最近追加された頂点の1近傍が集められ、少なくともk個の頂点がNに入るか、追加する近傍がなくなるまで続けられるものとなる。
1: input: vertex v, receptive field size k
2: output: set of neighborhood nodes N for v
3: N = [v]
4: L = [v]
5: while |N| < k and |L| > 0 do
6: L =
S
v∈L N1(v)
7: N = N ∪ L
8: return the set of vertices N3. Create Receptive Field:
1: input: vertex v, graph labeling `, receptive field size k
2: N = NEIGHASSEMB(v, k)
3: Gnorm = NORMALIZEGRAPH(N, v, `, k)
4: return Gnorm4. Graph Normalization:
ノードの受容野は、前のステップで組み立てられた近傍領域を正規化することによって構築される。正規化は近傍グラフのノードに順序を与え、順序のないグラフ空間から線形順序を持つベクトル空間にマップする。基本的な考え方は、グラフ内の構造的役割が類似している場合に限り、2つの異なるグラフのノードをそれぞれの隣接行列内の類似した相対位置に割り当てるグラフラベリング手順を活用することとなる。
1: input: subset of vertices U from original graph G, vertex v,
graph labeling `, receptive field size k
2: output: receptive field for v
3: compute ranking r of U using `, subject to
∀u, w ∈ U : d(u, v) < d(w, v) ⇒ r(u) < r(w) 4: if |U| > k then
5: N = top k vertices in U according to r
6: compute ranking r of N using `, subject to
∀u, w ∈ N : d(u, v) < d(w, v) ⇒ r(u) < r(w)
7: else if |V | < k then
8: N = U and k − |U| dummy nodes
9: else
10: N = U
11: construct the subgraph G[N] for the vertices N
12: canonicalize G[N], respecting the prior coloring r
13: return G[N]具体的なPATCHY-SANのコードはNiepertのgitページにて公開されている。
PATCHY-SANの課題
PATCHY-SANの課題としては、畳み込みが(学習ではなく前処理である)グラフラベリングに強く依存することと、ノードを1次元で順序づけすることが自然な選択であるとはいえないことが挙げられている。
また、グラフラベリングがグラフの構造だけを考慮しており、ノードの特徴を考慮していない点も課題として挙げられている。
参考情報と参考図書
グラフデータの詳細に関しては”グラフデータ処理アルゴリズムと機械学習/人工知能タスクへの応用“を参照のこと。また、ナレッジグラフに特化した詳細に関しては”知識情報処理技術“も参照のこと。さらに、深層学習全般に関しては”深層学習について“も参照のこと。
参考図書としては”グラフニューラルネットワーク ―PyTorchによる実装―“



“Graph Neural Networks: Foundations, Frontiers, and Applications“等がある。


コメント
[…] Spacialなグラフ畳み込みは、個々のノードとエッジで結ばれた周囲のノードの属性情報を集める操作を、畳み込み演算とみなして表現の学習を行うもので、”機械学習におけるメッセージパッシングの概要とアルゴリズム及び実装例“に述べているメッセージパッシングのグラフ畳み込みとも呼ばれているものとなる。代表的なアプローチとしては”PATCHY-SANの概要とアルゴリズム及び実装例について“で述べているPATCHY-SAN、DCNN(Diffusion-Convolutional Neural Network)、GraphSAGE等がある。 […]
[…] PATCHY-SANの概要とアルゴリズムについて […]
[…] それら理論的アプローチとして”How Powerful are Graph Neural Networks?“では、 “PATCHY-SANの概要とアルゴリズム及び実装例について“にて述べているWL同型テストと関連づけて以下のものを挙げている。 […]