Artificial Intelligence Technology Web Technology Knowledge Information Processing Technology Semantic Web Technology Ontology Technology Natural Language Processing Machine learning Ontology Matching Technology
The basic and global techniques introduced in the previous sections are the building blocks for constructing a matching system. Once the similarity or dissimilarity between ontology entities is obtained, all that is left is to calculate the alignment. This requires a more comprehensive process. In this chapter, we consider the following points in particular in order to build a practical matching system.
- Prepare to process large ontologies, if necessary.
- Organize combinations of various similarity and matching algorithms.
- Use of background knowledge sources.
- Aggregating the results of basic methods to compute compound similarity between entities.
- Aggregate the results of basic methods to compute compound similarity between entities.
- Learn a matcher from the data and tune it.
- Extract alignments from the resulting (dis)similarity: in fact, different alignments with different characteristics may in fact be extracted from the same (dis)similarity.
- Improve alignments by disambiguation, debugging, and repair.
Ontology Partitioning and Search Space Pruning
A matcher may have to deal with large ontologies containing tens or hundreds of thousands of entities. In order to do this efficiently, it can either partition the ontology into smaller ontologies and match those smaller ontologies, or dynamically ignore parts of the ontology during matching.
Partitioning
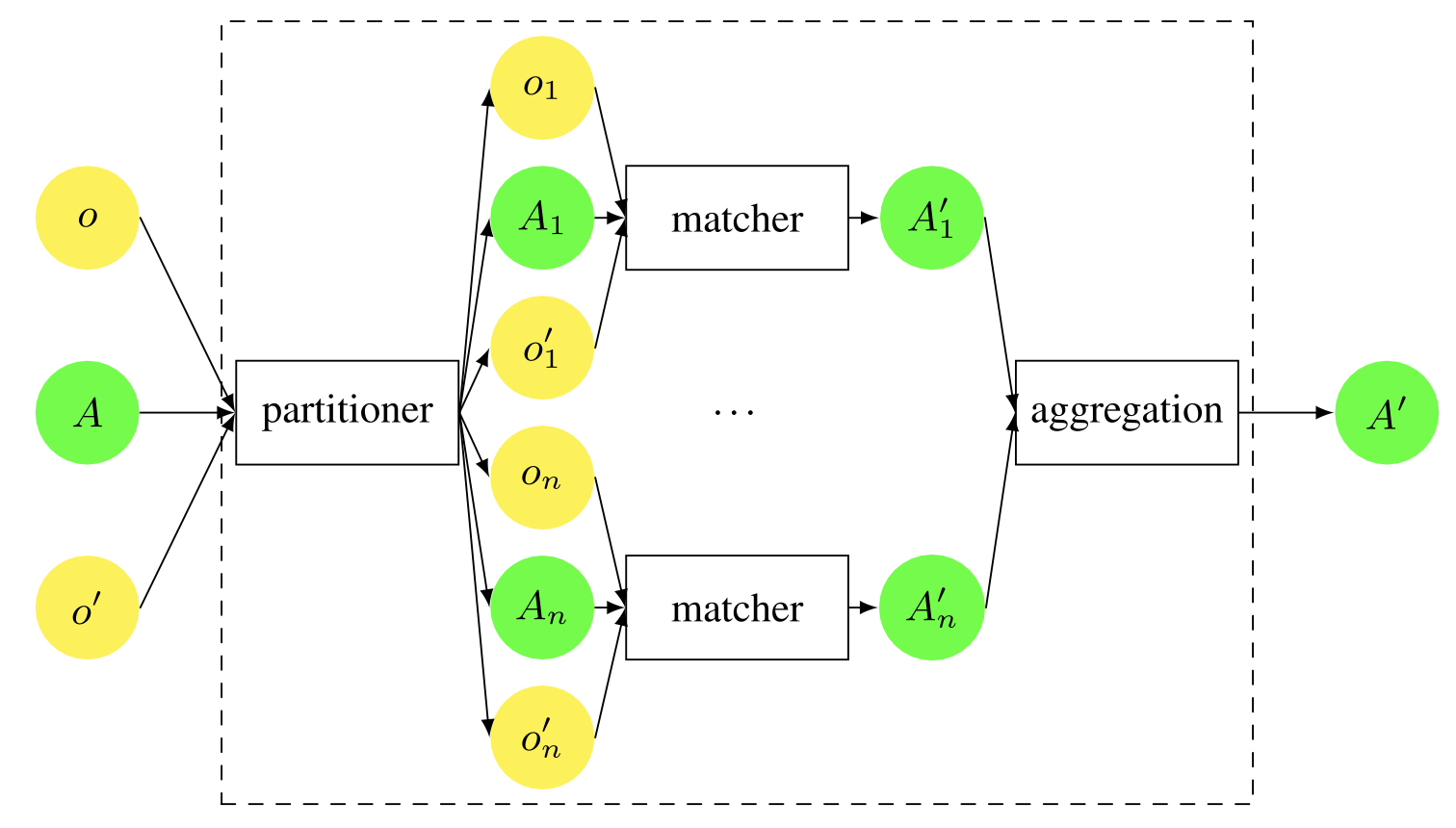
It is often useful to partition the part of the ontology that needs to be matched, perform partial matching, and then aggregate the results of the independent matching (usually accepting all the generated correspondences). This is illustrated in the figure below.

General principle of partitioning: the ontology to be matched is split into smaller ontology fragments, which are matched independently, and the results are merged.
We call this process ontology partitioning, which is not a strict mathematical partitioning, but a partitioning of a set of entities into exhaustive, non-overlapping classes. In fact, some parts of an ontology may be simply ignored because they have no counterparts in other ontologies.
Although the above figure is a simplification, some systems may perform iterative partitioning, for example, starting with the top-level entities and iteratively partitioning subclasses based on the results obtained. We may also work from the leaf entities towards the root.
This means dividing the ontology into blocks, avoiding the Cartesian product of comparisons between ontologies, and matching entities only from the corresponding blocks. Technically, blocking is performed by matching entities to a multidimensional index, where similar entities are placed close to each other in the index. Blocking is often used for interlinking data because of the large number of entities to be considered.
Anchors are often used in partitioning and pruning techniques. A relatively fast method for obtaining anchors would be to find entities with nodes that exactly match a certain hash function. To do so, instead of comparing all the nodes (complexity O(n2)), an index of all the entities in one ontology is built, typically via a hash table, and for each entity in the other ontology, it is possible to check if there is a corresponding indexed term This can be done by checking (complexity. O(2n)).
In partitioning, techniques developed for modularization of ontologies (Stuck- enschmidt et al., 1999) use the ROCK agglomerative clustering algorithm (Guha et al., 1999) for block-wise ontology Clustering. In this algorithm, two criteria are considered for designing blocks. Namely, the internal cohesion of the block and the pairing of the block with another block of another ontology. These are combined into a single measure of goodness, given two sets of classes (blocks) B and B′.
The link is a normalized similarity measure between the two classes, which is obtained quickly. Falcon-AO then pairs the blocks to be compared using a weighted sum of lexical similarity and Wu-Palmer similarity. The selection of pairs of blocks to be matched is based on the availability of anchors between them. These anchors are compared to the anchors of the other blocks. If this measure is better than a pre-defined threshold, the blocks are matched.
TaxoMap improves on the Falcon-AO method by providing two partitioning methods that attempt to introduce dependencies between two partitions (Hamdi et al. 2010b). The first algorithm, Partition-Anchor-Partition, first The second method, Anchor-Partition-Partition, is suitable for unstructured ontologies. This method splits the two ontologies, starting with the anchors found in the two ontologies, and in the second ontology, splits the group of anchors contained in the same block. In both cases, the blocks are paired based on the anchors. (Doran et al. 2009) report the benefits of different partitioning strategies to reduce the matching search space.
Partitioning can be used to parallelize matchers in simple paradigms such as MapReduce (Dean and Ghemawat 2004; Lin and Dyer 2010). In fact, each node can (1) partition the problem, (2) send each subproblem as soon as it becomes available to the node, (3) perform the map operation by aggregating the resulting subalignments, and (4) perform the reduce operation by simply matching two ontologies and returning the alignments This can be done. The hard part will be to find partitions that do not change the quality of the alignment by not providing enough information to the matcher. Conversely, redundant information can be removed in order to use less memory. The identified subproblems can also be cached permanently. Furthermore, this cache can be replicated to nodes in the cloud to facilitate parallel loading of the matching task.
Pruning of the search space (pruning technique)
The pruning technique will dynamically avoid partial comparisons without pre-partitioning the ontology.
AROMA learns association rules from general to more specific ones. At each stage, we can measure the maximum implication strength that can be obtained by learning more specific rules. If this value is below a threshold, the more specific rules are not considered and many comparisons can be avoided (David et al. 2007). Then, only further correspondences between two pairs of anchors given by previous techniques or previous fast equalization are investigated.
Lily defines reduction anchors that dynamically determine which comparisons to avoid (Wang et al. 2011): when two classes are in correspondence, a positive anchor prohibits the comparison of one subclass to the other superclass. A negative anchor prohibits the comparison of the neighborhood of a class with the neighborhood of a class with which it does not match (or is less similar).
Anchor-Flood also starts with an anchor, as above. Next, we compare the neighborhoods (or segments) of both anchors. That is, it compares the set of entities (parents, grandparents, children, grandchildren, siblings, etc.) connected to the anchor two levels ahead. The algorithm compares only the entities in two such anchored segments, starting from the anchor and spreading out in the neighborhood until it reaches all entities (Hanif and Aono 2009). Pairs of matching entities are reachable by the same type of operations (ascending, descending, siblings).
LogMap employs a two-fold strategy. First, it creates an index of all entities based on their labels and URIs. To enhance recall, it uses terminological techniques such as stemming and lexicon. From each pair of indexed entities, we extract candidate correspondences. Since only these candidate articles are eligible for matching, the pruning needs to be strong enough to limit the comparison, but weak enough not to overly restrict the range of the resulting alignments. Furthermore, since LogMap uses semantic methods, the ontology is partitioned and only the ontology modules relevant to each candidate correspondence are used for consideration. Similarly, PORSCHE and XClust first cluster entities to narrow down the searchable area of entities in the source ontology.
Matcher configuration
All of the steps described above can be considered as global methods. The purpose of a global method would be to combine local methods (or basic matchers) to define a new matching algorithm. Here, we present some natural ways to combine matchers at a strategic level. For this purpose, we will gradually introduce new graphical elements.
So far, we have only shown the outside of the matching process by creating an alignment from two ontologies, as shown in Figure 2.8. A natural way to construct a basic matcher is to improve the alignment using sequential composition (see Figure 7.2). For example, after using a label-based matcher (Section 5.2), we would like to perform a matcher based on the structure of the entity (Section 5.3) or a semantic matcher (Section 6.5).
 This sequential process can be used, for example, for online data integration. Ontology matching and integration is the integration of data (or in some cases data streams d and d′ ) represented by different ontologies (o and o′ ). To do so, the ontologies need to be matched in advance, and data integration can take advantage of this alignment. This is an example of combined offline and online matching.
This sequential process can be used, for example, for online data integration. Ontology matching and integration is the integration of data (or in some cases data streams d and d′ ) represented by different ontologies (o and o′ ). To do so, the ontologies need to be matched in advance, and data integration can take advantage of this alignment. This is an example of combined offline and online matching.
This can be considered as follows (see Figure 7.3).

Instance matching is another matching process that makes use of pre-matching ontologies (o and o′) in order to integrate data flows (d and d′). This is typically used in Figure 1.5 (Data Interlinking).
The first matching phase using the instance training set (f).
2. a data matching phase (f′) using the first alignment (A′).
In this setting, the second phase benefits from the precompilation of the first alignment. Indeed, the second matcher f′ can be thought of as a compilation of the first alignment.
However, the sequential combination of matchers is more classically used to improve alignment. If similarity or distance is used for this purpose, the matchers can be composed sequentially via their similarity matrix. In Figure 7.4, we see a new symbol for the matrix, a new component for extracting the initial matrix from the initial alignment or ontology pair (the first triangle), and another component for extracting the alignment from the similarity or dissimilarity matrix (the sparrow tail triangle, details are described in Section 7.7).
The sequential construction using the distance and similarity matrices is shown in Figure 7.5.

Introduction of a (virtual) matrix representing the similarity or distance measure between the entities to be matched. The first operator constructs an initial matrix M from the two ontologies o and o′ . The core operator of the matching algorithm generates a similarity or distance matrix M′ from this initial matrix and the ontology description. Finally, the alignment A′ is extracted from the matrix M′ .

Another way to combine algorithms would be to run several different algorithms independently and then aggregate the results. (See Figure 7.6). This is called parrel composition. These aggregation methods are very different and correspond to selecting one of the results based on some criteria or consolidating the results with some operator. For example, it is possible to run several matching algorithms in parallel and select the correspondences contained in all of them (intersection is used as the aggregation operator in this case), or select all of the most reliable correspondences.
In the latter case, it is often more convenient to define aggregation operators for the similarity and distance matrices (see Figure 7.7).

There are two main types of parallel synthesis.
In heterogeneous parallel synthesis, the input is split into different kinds of data (graphs, strings, sets of documents, etc.) and the aggregation either uses all of them (by aggregating the results) or only the most promising ones.
In the same kind of parallel synthesis, the input is sent to several competing systems, and the aggregate chooses the best of them or a consensus among them.
Of course, it will also be possible to combine these two classes further.
These combining techniques are usually implemented within a specific matching algorithm. However, there are also systems that provide the opportunity to combine other systems, for example, FOAM, Rondo, and the Alignment API.
In the next article, we will discuss context-based matching strategies.

コメント