AIの歴史と深層学習

AIの歴史と深層学習

まず人工知能(AI)についての定義を行う。人工知能(AI)が誕生したのは1950年台のことで、当時コンピューターサイエンスという新しい分野の草創に関わっていた一握りの先駆者たちは、コンピューターに思考させることが可能などうかについて考えを巡らしていた。この問いに対する答えは未だ出ていないが、この分野の定義を簡単にまとめるとすれば、「本来ならば人が行う知的な作業を自動化する取り組み」とすることができる。この概念は学習とは無関係な多くのアプローチを含んでいる。例えば初期のチェスプログラムは、プログラマーによりハードコーディングされたルールを組み込んでいるだけで、機械学習とは呼べものではなかった。

かなり長い間、多くの専門家は「人間に匹敵するレベルのAIを実現するには、知識を操作するのに十分な大量のルールを明示的に定義して、プログラマが手作業で組み込む必要がある」と考えていた。この考え方は、1950年台から1980年台の後半にかけてのAIの支配的なパラダイムとなっていた。それらのアウトプットとしてはエキスパートシステムがある。

チェスの試合のように、明確に定義された論理的な問題を特には、上記のアプローチは適していたが、画像分類、音声認識、言語の翻訳のように、より複雑でファジーな問題を解くための明示的なルールを突き止めるのは到底無理で、それらに変わる新しいアプローチとして、機械学習が生まれた。

機械学習の話の舞台はビクトリア時代のイギリスに遡る。エイダ・ラプレス伯爵夫人はチャールス・バベッジの友人であり、協力者であった。チャールズ・バベッジは、最初の汎用計算機として知られる解析機関(Analytical Engine)の発明者だった。解析機関は1830年台から1840年代にかけて設計され、時代をかなり先取りした先見の明はあったものの、汎用計算機として位置付けられたものではなかった。というのも、当時はまた「汎用計算機」という概念は存在していなかったためである。

解析機関は、数学解析分野の特定の計算を自動化するために機械的演算を使用する手段に過ぎなかった。解析機関と名付けられたのはそのためである。1843年、エイダはこの発明について「解析機関は、決して何かをつまり出すような気取ったものではない。実行させるためにどのように命令すればよいかが分かっているものであれば、何でも実行できる。解析機関の領分は、私たちがすでに理解しているものを利用できるようにするために手助けをすることにある。」と述べている。

エイダのこの発言は、後にAIの先駆者であるアラン・チューリングの1950年の歴史的な論文「計算する機械と知性(Computing Machinery and Intelligence)」において、「ラプレス伯爵夫人の反論」として引用されている。この論文では、チューリングテスト(Turing test)と、AIの原型となる主な概念が提唱されている。チューリングはエイダの発言を引用する一方で、汎用計算機が学習能力と創造力を持ちうるかどうかについて考察し、それは可能であるという結論に至っている。

機械学習は、次の課題に端を発している。それは「実行させるにはどのように命令すれば良いか分かっているもの」という枠を超えて、「特定のタスクの実行方法をコンピューターが独自に学習することは可能か」というものだ。これは、プログラマでデータ処理のルールを手作業で組み立てるのではなく、コンピューターがデータを調べてそうしたルールを自動的に学習することは可能なのかというものでもある。

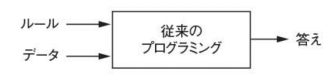
この課題は、新しいプログラミングパラダイムの扉を開くもので、従来のプログラムでは、ルール(プログラム)と、それらのルールに従って処理されるデータを人が入力すると、答えが出力される。(下図)

これに学習する機能を導入することで、データとそのデータから期待される答えを人が入力すると、ルールが出力され、そのルールを新しいデータに適用することで、新しい答えを生成することができる。(下図)

機械学習システムは、明示的にプログラムされるのではなく、訓練(train)される。タスクに関連するサンプルを大量に与えると、機械学習システムはそれらのサンプルから統計的な構造を抽出する。そして最終的には、そのタスクを自動化するためのルールの生成が可能となる。

例えば休暇中に撮った写真をタグ付けするタスクを自動化したいと考える。この場合、あらかじめタグ付けされた写真のサンプルを学習システムに与えると、機械学習システムが特定の写真を特定のタグに関連づける統計的なルールを学習することになる。

さらに、タグをつけた写真を何に使いたいのかという上位の意図を考えると、例えばアルバムを作るためには、アルバムレイアウトに合わせたタグ(写真)の選択をするためのルールを学習したり、過去の特定の記憶を再現したいという目的があった場合、それらを時系列に学習するということを行なったりする。

このような機械学習は数理統計学と深く結びついているが、重要な違いが双方にはある。深層学習等の機械学習は、ベイズ解析等の従来の統計解析と比較して、大規模で複雑なデータセット扱う傾向にあり、結果として、数学的な理論は影を薄め、エンジニアリングが重視されることとなる。機械学習は、アイデアが(理論にではなく)実験的に証明される実践的な分野となる。

ディープラーニング(deep learning)を定義し、機械学習の他のアプローチとの違いを理解するために、機械学習のアルゴリズムが「何をするのか」を理解する必要がある。先述したように、期待されるもののサンプルを機械学習に与えると、データ処理タスクを実行するためのルールが抽出される。従って、機械学習を実行するには、以下の3つのものが必要となる。

• 入力データ点:例えば音声認識タスクでは、これらのデータ点は会話を録音した音声ファイルとなる。画像タグ付けタスクでは、これらのデータ点は写真となる。
• 期待される出力の例:音声ファイルから人が書き起こした原稿や、画像タグ付けタスクでは、期待される出力は”dog”や”cat”といったタグとなる。
• アルゴリズムが良い仕事をしたかどうかを評価する方法:アルゴリズムの現在の出力と期待される出力との距離を特定する方法が必要となる。結果はアルゴリズムの動作方法を調整するためのフィードバックとして利用される。我々が「学習」と読んでいるのは、この調整ステップとなる。

機械学習のモデルは、入力データを意味のある出力に変換する。これは既知の入力と出力のサンプルから「学習」するプロセスとなる。したがって、機械学習とディープラーニングでは「データを意味のある形で変換すること」が主な課題となる。つまり、機械学習は与えられた入力データから有益な表現(representation)を学習する。それらの表現は、期待される出力に近づくためのものとなる。

ここで先に進む前に、表現とは何かについて考える。表現とは、データを表す(エンコードする)ためにデータを別の角度から捉える方法となる。例えばカラー画像はRGB(Red-Green-Blue)フォーマットかHSV(Hue-Saturation-Value)フォーマットでエンコードできる。これらは同じデータの2種類の表現となる。たとえば「画像の赤ピクセルをすべて選択する」タスクはRGBフォーマットの方が簡単であり、「画像の彩度を下げる」タスクではHSVフォーマットの方が簡単となる。

機械学習モデルの本質は、入力データに適した表現(分類タスクなど、データを現在のタスクにより適したものにする変換)を見つけ出すことにある。

具体的な例として、xy座標のx軸、y軸、それらの座標によって表される点について考える(下図)

この図には白い点と黒い点がいくつかある。点の(x,y)座標を取得し、その点が黒または城である可能性を出力するアルゴリズムを開発したとする。ここで必要となるのは、白い点と黒い点が明確に区別されるようなデータの新しい表現となる。さまざまな変換が考えられるが、そのうち一つは座標の変更となる。(下図)

この新しい座標系では、点の座標はデータの新しい表現であると言える。しかも良い表現となる。この表現では、黒と白の分離問題を「黒い点はx>0の点」「白い点はx<0の点」という単純なルールで表すことができる。この新しい表現により分類問題は基本的に解かれる。

上述の場合は、座標の変更を手作業で行ったが、そうではなく様々な座標の変更を体型的に調査し、正しく分類された点の割合をフィードバックとして使用したとする。その場合は、機械学習をお子なっていることになる。機械学習における「学習」は、よりよい表現を自動的に検索するプロセスを表す。

機械学習のアルゴリズムはどれも、そうした変換を自動的に見つけ出し、データほ特定のタスクにとってより有益な表現にすることで構成される。それらは上述のような座標の変換かもしれないし、線形投影かもしれないし、平行移動かもしれない(線形投影では情報が破壊されることがある)。あるいは「x>0の点をすべて選択する」といった非線形演算かもしれない。機械学習のアルゴリズムは、あらかじめ定義された一連の演算を一通り検索するだけであり、通常、そうした変換を検索するにあたって創造力を働かせることはない。このため予め定義された演算の集まりは仮説空間(hypothesis space)」と呼ばれる。

従って、技術的な定義では、機械学習とは「フィードバックのガイダンスに基づいて、予め定義された仮説空間内で入力データの有益な表現を検索する」ことになる。この単純な概念により、音声認識から自動運転まで、驚くほどに広い範囲に渡る知能的なタスクの解釈が可能となる。

次に「ディープラーニング」の定義について述べる。ディープラーニングは、データから表現を学習する新しいスタイルの機械学習となる。ディープラーニングでは、連続する層(layer)の学習に重点がおかれる。それらの層が深くなるほど、表現の重要性は増していく。ディープラーニングの「ディープ」は、このアプローチによって何らかの理解が深まる事を指しているのではなく。この「連続する表現の層」という概念を表している。

データモデルを構成する層の数は、そのモデルの深さ(depth)と呼ばれる。この分野については、階層化表現学習(layered representation learning)や階層的表現学習(hierarchical representation learning)と呼ぶ方が適切となる。近年のディープラーニングでは、表現の層が数十から数百にも重なっていることがよくある。そして、それらの層ではすべて訓練データから自動的に学習される。一方で、機械学習の他のアプローチでは、学習の対象を一つか二つの層からなるデータ表現に絞る傾向にある。このため、そうしたアプローチはシャローラーニング(shallow learning)または表層学習と呼ばれることもある。

ディープラーニングでは、こうした階層型の表現を(ほぼ常に)ニューラルネットワーク(neural network)と呼ばれるモデルで学習する。ニューラルネットワークはまさに層が積み重なった構造になっている。「ニューラルネットワーク」は神経生物学の用語で、ディープラーニングの中心的な概念の一部は脳に関する知識に基づいて開発されているが、ディープラーニングのモデルは脳のモデルではない。現代のディープラーニングモデルで使用されている学習メカニズムのようなものを脳が実装しているという証拠はどこにもない。大衆向けの科学誌でディープラーニングは脳と同じような仕組みになっているとか、脳をモデルにしているといった記事をみかけるが、それは正しくない。

この分野になじみのない人にとって、ディープラーニングは神経生物学と何らかの関係があると考えるのは問題の元であり、逆効果となる。人の心理のように神秘のベールで包み込む必要はない。ディープラーニングはあくまでもデータから表現を学習するための数学的な枠組みでしかない。

ディープラーニングアルゴリズムが学習する表現は、以下のような複数の層からなるネットワークがあるとしたとき

画像の数字を認識するための画像の変換は以下のように行われる。

このネットワークは、上図で示すように、数字の画像を表現に変換する。それらの表現は、元の画像から徐々に異なるものに変化しながら、最終的な結果に関する情報を少しづつ増やしていく。ディープニューラルネットワークについては、マルチステージの情報抽出演算として考えることができる。この場合、情報はフィルタを次々に通過することで徐々に「純化」されていき、何らかのタスクにとって有益な情報となる。

したがってディープラーニングとは、データの表現を学習するためのマルチステージの手法ということができる。これらの発想は単純だが、十分なスケーラビリティを持つため、魔法のように思えることがある。

ここまで述べたように、機械学習とは、画像などの入力からラベル”cat”などの目的値へのマッピングだということができる。このマッピングは、入力値と目的値などの様々なサンブルを観測することで表現される。また、ディープニューラルネットワークでは、入力値から目的値へのマッピングが単純なデータ変換(層)を深く積み重ねていくことによって実現され、そうしたデータ変換がサンプルからも学習される。

この学習がどのように行われているのかについて以下に述べる。

層がその入力データに対して何を行うのかに関する指定は、層の重み(weight)に格納される。基本的には、重みは一連の数字で表される。技術的には、層によって実装される変換はその重みによってパラメータ化される。(下図)

このため、それらの重みは層のパラメータ(parameter)とも呼ばれる。ひの場合の学習(learning)は、入力値を慣例する目的値に正しくマッピングするための重みの値を、ネットワーク内のすべての層に渡って見つけ出す事を意味する。しかし、ここで問題となるのは、ディープニューラルネットワークに数千万ものパラメータが含まれる可能性があることになる。それだけのパラメータごとに正しい値を見つけ出すのは気が遠くなる作業となる。さらに、あるパラメータの値を変更すると、その他すべてのパラメータの振る舞いに影響を及ぼす。

何かを制御するには、まず、その何かを観測できなければならない。ニューラルネットワークの出力を制御するには、その出力が期待されているものからどれくらいかけ離れているかを計測できなければならない。これを計測するのがネットワークの損失関数(loss function)となる。損失関数は目的関数(pbjective function)とも呼ばれる。損失関数は、ネットワークの予測値と真の目的値(ネットワークに出力させたい値)から損失率を計算する事で、そのサンプルでのネットワークの性能を補足する(下図)

ディープラーニングの基本的な原理は、損失率をΦ時バックとして使用する事で、重みの値を少しづつ調整していく、というものになる。重みの調整は、現在のサンプルにおいて損失率が低くなる方向に向かって行われる。

重みを調整するのはオプティマイザ(optimizer)になる。オプティマイザはバックプロぱゲーション(backpropagation)と呼ばれるアルゴリズムを実装する。バックプロパゲーションはディープラーニングの中心的なアルゴリズムであり、誤差逆伝播法とも呼ばれる。

ネットワークの重みは乱数値で初期化されるため、最初は単に一連のランダムな変換を実装するものとなる。当然ながら、ネットワークの出力は理想的な出力からかけ離れたものとなり、損失もかな高くなる。しかし、ネットワークがサンプルを処理するたびに、重みが正しい方向に毛買って調整され、損失関数が低くなっていく。これは訓練ループ(traning loop)と呼ばれ、訓練ループを十分な回数だけ繰り返す(通常は数千サンプルに対して数十回)、損失関数を最小化する重みの値が生成される。

次回はニューラルネットのHello WorldにあたるMNISTによる手書き文字認識について述べる。