主成分分析(Principle Component Analysis:PCA)について
近代深層学習技術の始まりであるオートエンコーダーについての項で、ヒントンらの論文では先行例としてPCAを述べていた。今回はそのPCAについてもう少し具体的に述べる。
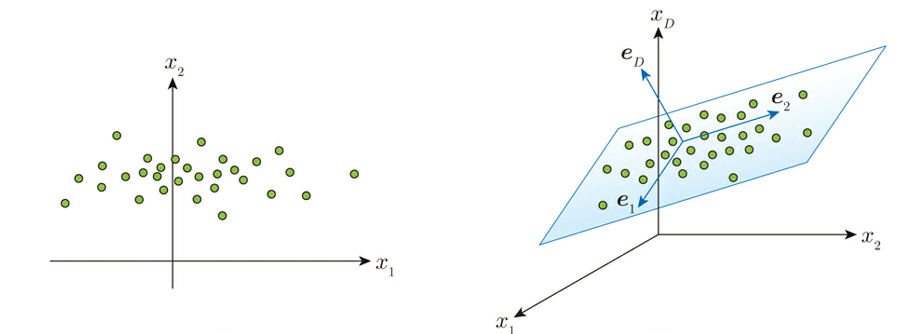
PCAは多次元のデータを次元圧縮する手法で、これは例えば2次元や3次元空間のデータを想定し、以下に示すようにある特定の1次元軸(直線)や2次元軸(平面)上でバラついている(分散が大きい)時、その直線あるいは平面上でデータが偏っているとして、元々あった2次元あるいは3次元の軸ではなく、特定の1次元軸(直線)や2次元軸(平面)上のデータとして表す事を言う。
機械学習プロフェッショナルシリーズ「これならわかる深層学習入門」より*1)
実際のアルゴリズムは、新たな部分空間(上述の特定の1次元とか2次元軸)を表す基底ベクトルeを想定し、データの分布の中央値(平均値)c0と共に使って最小か問題min E(c0, e)をラグランジュ未定係数法を用いて計算するものとなる。ラグランジュ乗数法の詳細に関しては”双対問題とラグランジュ乗数法“を参照のこと。
ここで実際にRを使って主成分分析を行ってみる。参考としたのは馬場真哉さんの「主成分分析の考え方」より
まずRがデフォルトで持っているiris(アヤメ)データを使って「ggplot2」と「GGally」の2つのパッケージを使ってグラフを書く。
install.pacjages("ggplot2")
install.packages("GGally")
library(ggplot2)
library(GGally)
ggpairs(iris, aes_string(color="Species", alpha=0.5))「ggpairs」という描画関数を用いて引数に「sea_string(color=”Specis”, alpha=0.5」を指定して種類ごとに色を付ける。alpha=0.5は透明度の指定となる。結果は以下となる。
それぞれの変数ごとに結果が表示されている。散布図はそれぞれの変数をxyとした時の分布、散布図と対象の位置にあるデータは相関係数、縦と横が同じ変数の場合はその変数の平滑化されたヒストグラム、最後の列は種類別の箱髭図となっている。
ここで主成分分析(「procomp」関数を利用)を実行する。
#種類データを除く(procompでは種類のデータに適用できない為)
pca_data <- iris[,-5]
#主成分分析の実行
model_pca_iris <- procomp(cpa_data, scale=T)
> # 結果
> summary(model_pca_iris)
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion 0.7296 0.9581 0.99482 1.00000
# 主成分分析の結果をグラフに描く
install.packages("devtools")
devtools::install_github("vqv/ggbiplot")
library(ggbiplot)
ggbiplot(
model_pca_iris,
obs.scale = 1,
var.scale = 1,
groups = iris$Species,
ellipse = TRUE,
circle = TRUE,
alpha=0.5 )
結果は以下となる。
iris pca結果
Petal.LengthとPetal.Widthはほぼ同じ軸を持つことが確認される。またSepal.Lengthも方向的にはかなり近いことが確認される。それに対してSepal.Widthは明らかに異なった方向の軸を持つことが目視できる。以上よりPetal.LengthとPetal.WidthそしてSepal.Lengthは第一主成分軸、Sepal.Widthは第二主成分軸であると判断できる。実際に上述のirisデータの分布を見てもSepal.Widthのみ他のパラメータと比較してヒストグラムの分布が異なっている。
PCAの発展系としては、対応分析(カテゴリデータなどにも適用可能)、カーネル主成分分析(非線形なデータにも適用可能)、主成分回帰(主成分分析をした結果を使って、回帰分析を行い、予測を行う)等がある。
参考文献 *1) これならわかる深層学習入門
また、”ロバスト主成分分析の概要と実装例“でも述べているロバスト主成分分析は、データの中から基底を見つけ出すための手法であり、外れ値やノイズが含まれているようなデータに対しても頑健(ロバスト)に動作することを特徴とするものとなる。
コメント
[…] Word2Vecは上記のようなしくみで各単語に相当する分散ベクトル表現を得ることができ、これとコサイン類似度を組み合わせると単語間の類似性が、前述したPCAやk-means等のクラスタリングツールを使うことでクラスタリングを行うことができる。 […]
[…] 分布仮説は、これに対して単語間の類似度に何らかの指標を与える仮説となる。これらに基づいた手法としては、word2vec、主成分分析(principle component analysis:PCA)、潜在ディリクレ配分(latent dirichlet allocation:LDA)等多々存在する。 […]
[…] まず主成分分析(priccipal component analysis、PCA)について述べる。PCAは線型空間におけるデータの分布をある基準で最もよく近似する、低次元の部分空間を求める次元削減方法となる。主成分分析に用いられる基準には、射影されたデータの分散最大化や、射影誤差の最小化などがあるが、いずれの基準を用いても得られる結果はほぼ透過となる。ここでは分散最大化を基準とした主成分分析について述べる。 […]
[…] 主成分分析 多次元データの次元圧縮手法 […]
[…] Rを使った主成分分析(PCA) […]
[…] 法(例: 主成分分析)を使用して、特徴空間の次元を削減することも効果的なアプローチとなる。主成分分析の詳細は”主成分分析(Principle Component Analysis:PCA)について“も参照のこと。 […]
[…] の呪いによる問題が発生することがある。k-meansを適用する前に、”主成分分析(Principle Component Analysis:PCA)について“で述べているPCAやt-SNEなどの次元削減手法を使用してデータを低 […]