k-meansの使いこなしの為のクラスタリングの評価について

クラスタリングの評価について

“深層学習だけではない、業務で使える「AIアルゴリズム」“でも紹介されていたが、k-meansは、簡便性、汎用性、データ取得性(ある程度少量のデータでも学習可能)と可読性の上からまずは適用してみるべきアルゴリズムの一つとなる。今回、そのk-meansの一段進んだ使いこなしの手法として、評価のテクニックについて述べたいと思う。(Clojure for Data Scienceより)

ライブラリにもよるがk-meanの評価を行うと、以下のような評価結果が付属されて出てくる。

Inter-Cluster Density: 0.6135607681542804
Intra-Cluster Density: 0.6957348405534836

理想的なクラスタリングは、クラスタ間の密度に比べて、クラスタ内の分散が小さいこと(あるいは密度が高いこと)となる。

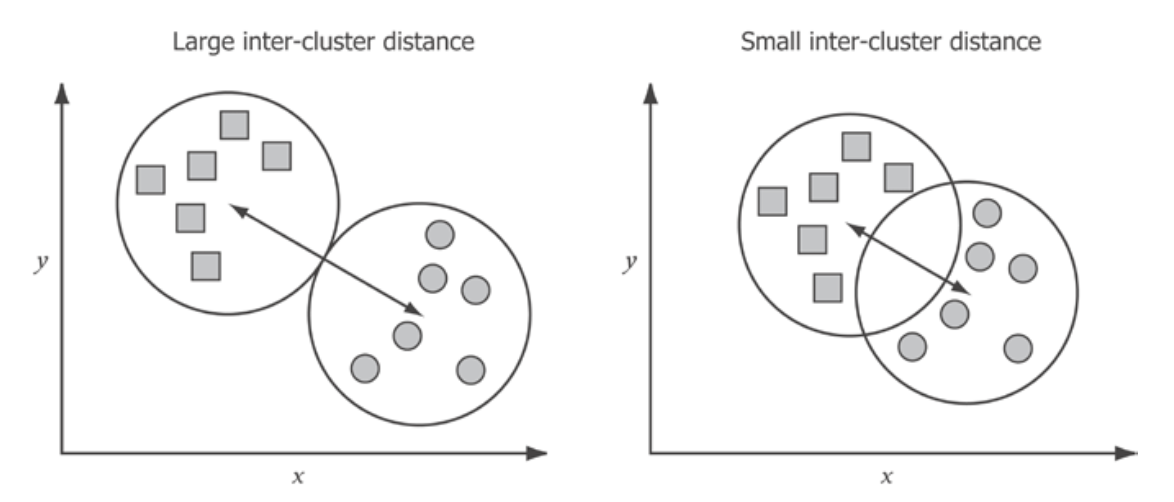
まずInter-cluster density(クラスタ間密度)とは、クラスタの中心間の平均距離のこととなる。良いクラスタは、中心が互いに近すぎることはない。もしそうであれば、クラスタリングによって類似した特徴を持つグループが作られ、サポートするのが難しいクラスタメンバー間の区別が行われていることを意味する。

Intra-cluster density(クラスタ内密度)は、クラスタがどれだけコンパクトであるかを示す指標となる。理想的には、クラスタリングは、互いに類似している項目のグループを識別する。コンパクトなクラスタは、クラスタ内のすべての項目が強く類似していることを示す。

したがって、最良のクラスタリング結果は、高いクラスタ内密度と低いクラスタ間密度を持つものとなる。しかし、データによっていくつのクラスタが正当化されるかは、必ずしも明らかではない。次の図は、同じデータセットをさまざまな数のクラスタにグループ化したものだが、理想的なクラスタ数を確信を持って言うことは難しい。

先ほどの図は意図的なものだが、データのクラスタリングに関する一般的な問題を示している。多くの場合、明確な「最適」クラスタ数は存在せず、最も効果的なクラスタリングは、データの最終的な用途に大きく依存する。

しかしながら、ある品質スコアの値がクラスタ数によってどのように変化するかを判断することによって、どの値がより良い値であるかを推測することはできる。品質スコアは、クラスタ間密度やクラスタ内密度のような統計値とすることができる。クラスタ数が理想に近づくと、この品質スコアの値が向上することが予想される。逆に、クラスタ数が理想から乖離すると、品質が低下することが予想される。したがって、データセット中のクラスタ数の妥当性を知るためには、kの値を変えて何度もアルゴリズムを実行する必要がある。

二乗誤差

クラスタ品質の最も一般的な測定方法の1つは、二乗誤差の合計（SSE）となる。各ポイントについて，誤差は最も近いクラスタセントロイドへの測定された距離である．したがって、クラスタリングSSEの合計は、クラスタ化された点からその対応する中心値までのすべてのクラスタにわたる合計となる。(RSME((Root Mean Squared Error))

\[RMSE=\sqrt{\frac{1}{n}\displaystyle\sum_{i=1}^k\sum_{x\in S}||\mathbf{x}-\mu_i||^2}\]

ここで、μiはクラスタSiの中心値(平均)、kはクラスタの総数、nはポイントの総数となる。

RMSEをクラスタ数に対してプロットすると、クラスタ数が増えるにつれて減少していく。クラスタが1つの場合、RMSE誤差（元のデータセットの平均からの分散）が最も大きくなり、一方、RMSEが最も小さくなるのは、すべての点がそれ自身のクラスタ内にある場合の縮退（RMSEゼロ）となる。これらの両極端は、明らかにデータの構造をうまく説明することができない。しかし、RMSEは一直線に減少するわけではない。クラスタ数を1から増やすと急激に減少し、「自然な」クラスタ数を超えると緩やかに減少する。

そこで、理想的なクラスタ数を判断する一つの方法として、クラスタ数に対してRMSEがどのように変化するかをプロットする方法がある。これはエルボー法と呼ばれる。

エルボー法を用いた最適なk値の推定

エルボー法を用いてkの値を決定するためには、k-meansを何度も再実行する必要がある。以下の例は、2から21までのすべてのkについて計算したものとなる。

上図ではkが13クラスタ程度を超えるとRMSEの変化率が鈍化し、さらにクラスタ数を増やすと少なくなることがわかる。従って、このグラフからは、13クラスタ程度が適切であることがわかる。

エルボー法は直感的に理想的なクラスタ数を決定することができる方法となるが、実際には適用が難しい場合がある。kが小さい場合やRMSEにノイズが多い場合、エルボーがどこに位置するのか、あるいはエルボーが存在するのかがわからない場合があるからである。

クラスタリングは教師なし学習アルゴリズムなので、クラスタの内部構造がクラスタリングの品質を検証する唯一の手段であるとここでは仮定する。真のクラスタラベルが既知であれば、外部検証手段（エントロピーのような）を用いて、モデルの成功を検証することが可能となる。

他のクラスタリング評価スキームとして、DunnインデックスとDavies-Bouldinインデックスについて述べる。どちらも内部評価スキームであり、クラスタ化されたデータの構造のみを見ることを意味する。それぞれ、最もコンパクトでよく分離されたクラスタを生成したクラスタリングを特定することを目的としており、その方法は異なる。

Dunn指標による最適なk値の推定

Dunn指標は、最適なkの数を選択する別の方法を提供する。Dunn指数は、クラスタリングされたデータに残る平均誤差を考慮するのではなく、2つの「最悪の場合」の比率を考慮する(2つのクラスタ中心間の最小距離、最大クラスタ直径で割ったもの)。一般に、クラスタ間距離は大きく、クラスタ内距離は小さくしたいので、この指数が高いほど良いクラスタリングであることを示している。

k個のクラスタに対して、ダン指数は次のように表現できる。

\[DI_m=\frac{\min_{1≤i<j≤k}\delta(C_i,C_j)}{\max_{1≤m≤k}S_m}\]

ここで、δ(Ci,Cj)は2つのクラスタCiとCjの距離、max1≦m≦k Smは最大クラスタの大きさ（または散らばり具合）を表す。

クラスタの散らばり具合を計算する方法はいくつか考えられる．クラスター内の最も遠い2点間の距離，クラスター内のデータ点間のすべてのペアワイズ距離の平均，またはクラスターの中心値自体からの各データ点の平均を取ることができる．

dunn-index関数を用いて、k=2からk=20までのクラスタの散布図を作成すると以下のようになる。

ダン指数が高いほど、より良いクラスタリングであることを示す。したがって、最も良いクラスタリングはk=2、次いでk=6、そしてk=12とk=13がその後に続く。

Davies-Bouldin指標による最適なk値の推定

Davies-Bouldin指数は、クラスタ内のすべての値について、大きさと分離の比率の平均を測定する代替評価スキームとなる。これは、各クラスタについて、クラスタサイズの合計をクラスタ間距離で割った比率が最大となる代替クラスタを見つける。Davies-Bouldin指数は、この値をデータ中の全クラスタについて平均化したものと定義される。

\begin{eqnarray}D_i&=&\max_{i≠j}\frac{S_i+S_j}{\delta(C_i,C_j)}\\DB&=&\frac{1}{n}\displaystyle\sum_{i=1}^n D_i\end{eqnarray}

ここで、δ(Ci,Cj)は2つのクラスタ中心CiとCjの距離、SiとSjは散らばり具合である。ここで、クラスタk=2〜k=20のDavies-Bouldinを散布図上にプロットした例を示す。

Dunn指数とは異なり、Davies-Bouldin指数は、サイズがコンパクトで、クラスタ間距離が長いクラスタを探す優れたクラスタリングスキームとなる。上記の結果からk=2が理想的なクラスタサイズであり、次いでk=13であることがわかる。

K-meansの最適化について

k-meansは、その比較的容易な実装と、非常に大きなデータセットにもうまく対応できることから、最も人気のあるクラスタリングアルゴリズムの1つとなる。しかし、その人気にもかかわらず、いくつかの欠点がある。

その欠点の一つが、k-meansは確率的であり、クラスタリングの大域的最適解を見つけることは保証されないことにある。実際，このアルゴリズムは外れ値やノイズの多いデータに対して非常に敏感であり，最終的なクラスタリングの質は，最初のクラスタ中心点の位置に大きく依存することがある。これは言い換えれば、k-meansはグローバル・ミニマムではなくローカル・ミニマムを定期的に発見するものということができる。

マハラノビス距離

赤い点のデータ群があるときに、青い点と緑の点のどちらがデータ群から離れているかを考える。データ群の平均(Xの点)からのユークリッド距離を考えると、緑と青の点はほぼ同じ距離となる。しかしながら、緑の点の方がデータ群から離れていると考える方が自然な解釈となる。

これはデータ群からの距離を考える際に、単純な距離だけではなく、データの各方面への散らばりまで考えた指標が必要であることを示唆している。これを実現するものがマハラノビス距離となる。定義としては、データ群の平均ベクトル\(\vec{\mu}\)、分散共分散行列がΣであるとするとき、あるベクトル\(\vec{x}\)のマハラノビス距離として以下のように表される。

\[d_{Mahalanobis}=\sqrt{(\vec{x}-\vec{\mu})^T\Sigma^{-1}(\vec{x}-\vec{\mu})}\]

各変数のマハラノビス距離を測ることで、クラスタから明らかに離れたポイント(異常点)を判定することができる。

例として以下のようなデータがあったとき(矢印が異常点)

各変数のユークリッド距離を測ると以下のようになり、どの点も差がつかない。

マハラノビス距離でプロットすると以下のようになり、一点だけ大きく外れることが確認できる。

データが一次元の場合は、平均ベクトルはスカラーμ、分散共分散行列もスカラーσ2となる。よってマハラノビス距離は以下のようになる。

\[d=\sqrt{(x-\mu)\cdot\frac{1}{\sigma^2}\cdot (x-\mu)}=\frac{|x-\mu|}{\sigma}\]

これは平均との差を標準偏差σで正規化したものとなり、絶対値を取り除いた\(\frac{x-\mu}{\sigma}\)はzスコアーという名前で知られているものとなる。

次元の呪い

マハラノビス距離尺度が克服できない課題が「次元の呪い」として知られている。これは「データセットの次元数を増やしていくと、すべての点が他の点から等しく遠くなる傾向」のことを言う。例えば100点の合成生成データセットにおいて、最小距離と最大距離の差を求めたものが以下の図になる。次元数が集合の要素に近づくと、各要素の組の最小距離と最大距離が近づいていき、100次元、100点のデータでは、どの点も他の点から等しく離れるようになる。

なおpythonでのk-meansに関しては”k-meansの概要と応用および実装例について“を参照のこと。