機械学習技術について

機械学習技術について

機械学習とはwikiによると「経験からの学習により自動で改善するコンピューターアルゴリズムもしくはその研究領域」と定義される。人間が自然に行っている学習能力と同様の機能をコンピューターで実現しようとする未来の技術であるとも言え、「学習能力とは何か?」を本質的に考える基礎研究でもあり、哲学的な側面を持つアプローチでもある。 それに対して近年ではデータ活用に重点をおいたより工学的な立場の定義である「機械学習」が多く用いられている。データの特徴を数学的に解析して、データに潜む規則や構造を抽出することにより、未知の現象に対する予測やそれに基づく判断を行うという実用に重点をおいたものとなる。

このような工学的な観点においては、物事や現象の中から、多くの訓練データを学んでその中にあるパターンやルールを見つけ出す作業を行うことが基本的なプロセスとなる。このようにデータから学習するということは、訓練データが何らかの規則に従って生成されているときに、データを生成する規則をなるべくよく模倣し、再現するという作業となるとも言える。

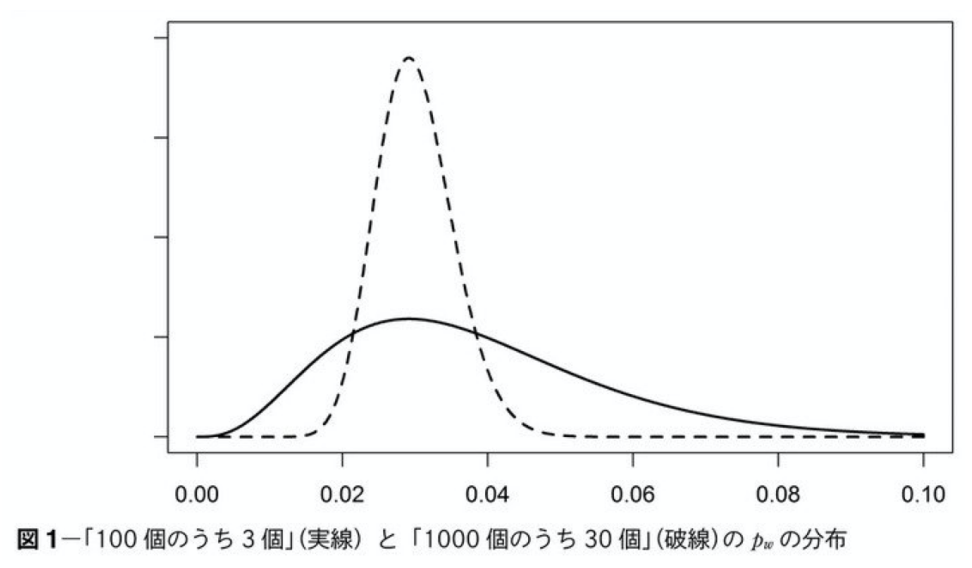
機械学習はこれをコンピュータが持つ計算機という機能を使って行うものとなる。これは、訓練データを単にそのまま記憶していくというものではなく、その背後にあるモデル(パターンやルール)を明確にすることで(抽象化する)、訓練データ以外のデータが入力された時にそれを判定できるようにするという作業となる。このような作業は汎化と呼ばれる。 機械学習のモデルには、線形回帰モデルのような非常にシンプルなものからパラメータの数が数万もある深層学習まで様々なものが提案されている。これらの中で何を用いるべきかは、観測されるデータ(サンプル数や特性等)や学習の目的(単なる予測なのか、結果の説明まで必要なのか等)に依存する。 上記のデータや目的に対して必要とされるモデルが異なるケースを例を示す。まずデータについて、下図に同じ正解率でサンプル数が異なる場合のベイズモデルでの確率分布を示す。 共に3%が正解のデータの正規分布を示す。波線がサンプル数が1000個で正解が30のケース、実線がサンプル数が100個で正解が3個を表す。上記から分かるように、サンプル数が少ない場合は裾が大きく広がり、3個の正解以外も正解である確率が増加する。(ばらつきが増加する)。 深層学習のようなパラメーターが膨大にある複雑なモデルを使うと、一見全ての特徴を捉えることができるようにも考えられるが、上記に示すようにそもそもの訓練データが少ない場合は、それぞのパラメータに対してのばらつきが大きくなるため、沢山の不確定要素が介在し、それぞれのパラメータの持つばらつきの影響が大きくなって、正解でない答えを選んでしまう確率が高くなる。そのため、このようなサンプル数が少ない場合にはスパースモデルのような少ないパラメータで答えを出すモデルの検討が必要になる。(現実のケースではサンプル数が少ないケースの方が多い) また、タスクの目的が単純なデータの予測ではなく、なぜそのデータになっているのかを求められるようなケース(例えば予測されたデータに対して判断が要求されるようなケース)でも、大量のパラメータを使ったブラックボックス的アプローチではなく、ある程度厳選されたデータで表現されたホワイトボックス的なアプローチが求められる。 これらをまとめると現実のタスクに機械学習を適用するためには、以下の3つの課題を考える必要がある。

1. その問題をどのように解きたいのか(なぜその問題が生じているのか等の根本問題を含む)
2. 具体的にどのようなモデルをあてはめれば良いのか(各種モデルの検討)
3. それらモデルを現実的な計算手段でどうやって計算するのか(アルゴリズム)

まず1に関しては、どのような切り口でデータを解釈したら良いのか?を明確に定義する必要がある。この目的の明確化は、要件定義と呼ばれる作業となる。一般的に用件定義は、対象となるドメイン(業務を対象とする場合には業務フロー)を分析し、その中から課題を抽出して、その課題を解決する機能を定義するものとなる。この課題のシステマチックな分析の手法がKPIやOKR等になる。

次に2に関しては、多数のパラメータに対応したければ深層学習モデルが、単一の結果ではなく複数の結果を得たければ確率生成モデル、連続的にデータを得ながら学習したいのであればオンラインモデル、また学習結果とその評価値を組み合わせた強化学習等様々なものが提案されている。本ブログではこれらに対して、現代の機械学習のブレークスルーと呼ばれている、深層学習法、カーネル法、スパースモデリング等の手法を中心に幅広く述べている。

最後に3に関しては、確率的生成手法で用いられているベイズの定理に代表される各種確率的理論、深層学習における逆伝搬法や、スパースモデリングに用いられているノルム正則化等様々な数学的理論に基づいた効率的な計算や各種アルゴリズムの適用が必要になる。

実用という観点での、機械学習のタスクとしては以下のようなものがある。

1. 回帰(regression) : ある入力から連続値の出力を予測するための関数を求める。線形回帰が最も基本的な回帰。(パラメータが入力ベクトルを足し合わせて変換することから「線形回帰」と呼ばれる。
2. 分類(classification) : 出力を有限個のシンボルに限定したモデル。様々なアルゴリズムがあるが、一例として実際の計算を行うときには、シグモイド関数等を用いたロジスティック回帰等が行われる。
3. クラスタリング(clustering) : 入力データを、何らかの基準に従ってK個の集合に分けるタスク。様々なモデルとアルゴリズムがある。
4. 次元削減(linear dimensionality reduction) : 現実の系ではよく見られる高次元のデータを処理するために行う。行列計算等の線形代数をベースとして行うものが基本。
5. 信号系列等の時系列データの分離 : 確率的モデルをベースにデータの繋がりを予測するタスク。次に何が出で来るかをリコメンドしたり、データの欠損を補間したりするタスクとしても利用される。
6. シーケーンスパターン抽出 : 遺伝子やワークフロー等のシーケーンスパターンを学習する
7. 深層学習 : 数千から数億のパラメータを学習するタスク。画像処理等で成果が上がる。

ほとんどの機械学習は以下の3つのステップから構成される。抽象化(abstraction)と呼ばれるデータから特徴量を抽出するステップ、汎化(generalization)と呼ばれる特徴量からのパターンの抽出(例えば分類)のステップ、評価(evaluation)と呼ばれる学習した知識の有意度を測定し、改良を促すフィードバックメカニズムからなるステップ。例えば、近年話題になった深層学習は、これらのうち最後のステップにブレイクスルーがある技術であると言える。

機械学習の実施には大きく分けて2つのアプローチがある。一つは「ツールボックスとしての機械学習」。様々なアルゴリズムに基づいて作られたツールを選びデータを導入して、何らかの基準に従って性能評価の良いアルゴリズムを選ぶことで最終的な予測や判断を行うもので、高度な数学の知識がなくとも多少のプログラミング技術があれば機械学習システムを構築可能なアプローチとなる。

もう一つは「モデリングとしての機械学習」で、データに関するモデル(仮説)を事前に構築して、それらに含まれるパラメータや構造をデータから推論するものである。モデリングの手法としては、統計的な手法(生成モデル)と、ツールボックス的手法の拡張である深層学習系の2つがあり、いずれの手法もモデルを計算する為の数学的手法を十分に身につける必要があり、ハードルは高いが、適用の自由度は広がる。

最近のDNNの隆盛により、従来の人工知能であるシンボリックなアプローチは「フレーム問題」があって「使えない技術」であり、機械学習ではそれの問題は全て解決してデータさえ集めればなんでも答えが出てくるという「機械学習絶対主義」的な人が増えたと感じる。特に若い人にその傾向は強いと思う。

しかしながら、そもそも人間の思考はシンボリックな情報と切っても切れないものであり、それらをを否定することは、数学や物理そのものを否定することにつながることになるのではないかと思う。

また、フレーム問題の本質は、「有限の情報処理能力しかない機械は、現実に起こりうる問題全てに対処することができない」ことを示すものであり、これはシンボリックであろうが、機械学習であろうが全ての「機械が行う処理」に当てはまるものではないかと思う。実際に機械学習にも「ノーフリーランチ定理(no-free-lunch theorem)>」というものがあり、領域の定義を行わなければ最適化はできないという「フレーム問題」と同様な問題はある。

下図は、様々な機械学習手法で分類のタスクを行ったものを示したものであ。(skit-learn:Comparing different clustering algorithms on toy datasets)

同じデータでも、学習アルゴリズムにより結果が異なっているのがわかると思う。

本ブログではこれらさまざまな機械学習技術に関して以下の項目について述べている。

Chinoba

Chinoba

Intelligence as Relationship

Research Platform

founded by

Masao Watanabe

AI Systems Architecture
Decision Trace
Human–AI Coordination
Algorithmic Governance