プログミングにおけるデータの型と静的型付け言語、動的型付け言語
型理論(Type theory)とは、プログラミング・数学・言語学等に現れる型の概念及びそれらが成す型システムを研究対象とする数学・計算機科学の分野である。特定の型システムのことを型理論と呼ぶこともある。集合論の代替となる数学の基礎として役立てられる型理論(型システム)も存在する。そのような例としてアロンゾ・チャーチの型付きラムダ計算やマルティン・レーフの直観主義型理論が有名である。
20世紀初頭にバートランド・ラッセルが発見した、ラッセルのパラドックスによるフレーゲの素朴集合論の欠陥を説明する中で提起されたtheories of typeが型理論の起源であり、後年にAxiom of reducibilityが付随された型理論は、ホワイトヘッドとラッセルの 『プリンキピア・マテマティカ』に収録されている。
また”人工無脳が語る禅とブッダぼっど“ではラッセルの「プリンキア・マテマティカ」を読んでさらに考察を深めたウィトゲンシュタインによる言葉の型と意味との関係を禅の思想に絡めて述べている。
さらなる数学的アプローチとしては、”現代思想2020年7月号 特集=圏論の世界 ――現代数学の最前線 読書メモ“で述べているような圏論とも関連するものとなる。
今回は、ソフトウェアデザイン2020年5月号より、コンピューターにおける型の基本として、プログミングにおけるデータの型と静的型付け言語、動的型付け言語について述べる。
コンピュータはデータをどう扱うのか
プログラミング言語には「データ型」がつきものとなる。データ型といえば読んで字の如く「データの型」のことだが、まずはそもそもコンピュータは「データ」をどのような形で保持するのかについて述べてみる。
コンピュータは基本的には数値しか扱えない。例えば文字を扱うばあでも、文字に番号(文字コード)を振ってそれを扱うことになる。そして、その数値は2進数で表現する。2進数というのは、我々が普段扱う10進数が「0〜9の数字を使い9の次は10に繰り上がる」のに対して「0と1だけを使い1の次は10に繰り上がる」という表現方法となる。10進数ならすべての桁が9になると次の桁に繰り上がるが、2進数ではすべての桁が1になると次の桁に繰り上がる。よって2進数なら、0と1だけで、例えば8桁なら0〜255までの数を表現できる。
現在のコンピュターのメモリはDRAMといって、とても小さな蓄電器(コンデンサ)の集合体だが、このコンデンサが電荷を帯びていれば1、帯びていなければ0と見なすことで、2進数の1桁(ビット)を表現できる。大抵は8ビットを1単位としてメモリを管理しており、これをバイトと呼ぶ。
ここまでだと整数しか表現できないが、小数を含む数は、数の大小にかかわらずある程度の精度で表現できるよう、通常は浮動小数点数という形式で表現する。現在は、IEEE754という規格で定められた形式を使うことがほとんどで、32ビット(4バイト)で表現する形式を単精度、64ビット(8バイト)の形式を倍精度と呼ぶ。
そして、メモリにはバイト単位で番地が振られており、この番地のことをアドレスと呼ぶ。
C,Java,C#などにおける型
上述のように、2進数やIEE754で整数や浮動小数点数を表現できる。そういった値を格納するのが変数であり、C、C++、Java、C#といった静的型付け言語では、変数に型がある。例としてCの代表的な型を以下に挙げる。
- char : 1バイト
- short : 2バイト
- int : 4バイト
- long : 8バイト
- float : 4バイト
- double : 8バイト
上記のバイトはデータのサイズとなる。Cの場合はそれぞれの型が具体的に何バイトであるのか規格に定められていないため、今時のPCの処理系での値を示している。変数とは値を入れる箱のようなものであり、charやshortといった型は、変数の箱のサイズを決めているとも言える。
また、処理系がメモリの値を解釈するときにもデータ型は必要で、たとえば2進数の0011111100011001100110011001100は、整数(init)として解釈すると1066192076を意味するが、浮動小数点数(float)として解釈すると、1.1を意味している。型を指定することで、処理系が正しく値を取り出すことができるのである。
列挙型
たとえばワープロやブラウザなど、何らかの文字列を表示するプログラムを作っているとして、文字列を行内で左寄せで表示するか、センタリングするか、右寄せで表示するかという情報(水平位置)を、何らかの変数に保持したいとする。
こういうとき、例えば左詰めはわ、センタリングは1、右詰めは2と決めれば、int型の変数で水平位置を表現できる。これが0と1と2ではなくC言語のように次のように定数を定義するケースもある。
const int H ALIGN_LEFT = 0;
const int H_ALIGN_CENTER = 1;
const int H_ALIGN_RIGHT = 2;これで良さそうにも見えるが、ここで表現したいのはあくまで「水平位置」であって、水平位置は本来はint型ではない。このように「いくつかある中のいずれかの値を取る型」として、Cでは列挙型という型が用意されている。列挙型は、Cでは以下のように宣言される。
typedef enum {
H_ALIGN_LEFT,
H_ALIGN_CENTER,
H_ALIGN_RIGHT,
} HorizontalAlignment;このように宣言しておけば、以降は以下のようにして「水平位置型」の変数(下の図はalignment)を宣言できる。
HorizontalAlignment alignment;intやdoubleなどといった型は、プログラミング言語に最初から組み込まれた型だが、列挙型では、このようにプログラマが定義する型となる。列挙型は内部的には単なるInt型だったりするが、列挙型を使うことでプログラムの可読性を上げることができる。
JavaはJava5(Tiger)に至るまでは列挙型は無かった。そのため、JavaでGUIを作るための昔からのライブラリであるAWT(Abstract Window Tollkit)では、ラベルの文字列の水平位置を整数で指定している。よって、水平位置を指定するためのメソッドは以下のようになっている。
public void setAlignment(int alignment)これではこのメソッドを使う側は何を渡せば良いかわからないため、Java5にて列挙型が導入された。
複合型
ここまでの型は、すべて1つの変数で一つの値を表す型でプリミティブ型と呼ばれるものだったが、それに対し、複数の値を含む大きな型を「複合型」と呼ぶ。複合型としてまず挙げられるのが、配列型でC,Java,C#などの言語では、配列型とは、ある一つの方が複数連なった型といえる。
もう一つの複合型は、Cなら構造体(struct)型、C++やJavaやC#ならクラスと呼ばれる型となる。構造体型やクラスでは、複数の型を組み合わせて新たな型を作ることができる。例えば「人」の情報を表現するPerson型なら以下のようになる。
<C Case>
typedef struct {
char name[32];
int age;
} Person;
<Java Case>
class Person {
String name;
int age;
}ここで定義したPerson型は、人の名前(name)と年齢(age)を保持できる形なる。Cの法は、配列nameのサイズが32となっているので、名前の長さは上限32バイトなる。
値型と参照型
上の例を見ると、CもJavaも大差ないように見えるが、Person型の変数pを宣言した時の意味は大きく違う。
Cの場合は、Person型の変数は値型であり、それ自体にnameとageを含む。これを変数の箱に例えると、変数自体が大きな箱となる。よって以下のように変数pを宣言すれば、すぐにそれに値を格納できる。
Person p;
/* p.nameに"C太郎をコピーする*/
strcpy(p.name, "C太郎");
/* p.ageに48(Cの年齢)を設定する*/
p.age = 48;
それに対してJavaでは、変数は、「箱」を指し示すための参照値だけを保持する。そのため、Javaではpを宣言するだけではp.namwなどに値を格納することはできず、以下のようにnewによりPersonのメモリを確保して、pをそこに向ける必要がある。
Person p;
//Person分のメモリを確保し、pをそこに向ける
p = new Person();
//p.nameを「Java太郎」に向ける
p.name = "Java太郎";
//p.ageに25(Javaの年齢)を設定する
p.age = 25;これを図にすると、以下のようになる。

Javaでは、クラスや配列は参照型であり、参照型の変数は参照値だけを格納する。参照値とは、対象とするデータを「指し示す」値であり、上図では矢印で表現している。文字列もsytingクラスというクラスなので、参照型となる。それに対して、intやdoubleはプリミティブ型であり、こちらは変数が値を直接保持する。
なお、C#では、クラスと構造体の両方をサポートしているので、Person型のような複合型を直接含む変数も作ることができる。DateTime(日付)型のような小さな型は、構造体とすることが多い。Cでも、pを参照型にすることは可能で、次のように*をつけてポインタ型として宣言すればよい。newの代わりに、malloc()関数でPerson分のメモリを確保する。
Person *p = malloc(sizeof(Person));Cのポインタ型というのは、メモリのアドレスを格納する為の型となる。最近のPCであれば、ポインタのサイズは8バイト(64ビット)となる。Javaなどの参照型も、同様にアドレスを格納する。最近のプログラミング言語が使うメモリは、静的領域とスタックとヒープに大きく分けられる。

静的領域というのは、グローバル変数や、static宣言した変数の値が格納される領域となる。静的領域は、原則、プログラムの最初から最後まで存在し続ける。
スタックというのは、”グラフデータの基本的アルゴリズム(DFS、BFS、ニ部グラフ判定、最短路問題、最小全域木)“でその構造を述べているが、ローカル変数を保持する領域となる。ローカル変数はそのメソッドを抜けるまでしか使わないので、メソッドを抜けたら縮む。ローカル変数にスタックを使うことで、現在動いていないメソッドのローカル変数分の領域が節約できるし、再帰呼び出しも可能となる。
ヒープは、Cならmalloc()関数、JavaやC#ならnewで確保する領域となる。不要になれば、Cならfree()関数でプログラマが解放するが、JavaやC#であれば大抵GC(ガーベージコレクタ)が用意されており、自動で解放してくれる。GCの処理系が何をもって不要と判断するかは「静的領域やスタックから辿れなくなったこと」が当てはまる。
ここでヒープとは、「子要素は親要素より常に大きいか等しい(または常に小さいか等しい)」という制約を持つ木構造」のことを呼び、この構造の特性を使ったソーティングが”データのソート(並べ替え)について“でも述べているヒープソートとなる。
Cなら、静的領域やスタックに配列や構造体を直接格納できるが、Javaでは、配列やクラスのオブジェクトはすべてヒープに格納される。上図ではヒープのオブジェクトを円で表現しているが現実のメモリ領域ではこのように浮かんでいるわけではなく、メモリ1次元に並んでいて、1バイトきざみでアドレスが割り振られており、そのアドレスの値が参照値であり、参照型の変数はそれを格納する。
そのような観点で見ると、常に存在し続ける静的領域や、メソッド呼び出しに応じて伸び縮みするだけのスタックに比べ、ヒープの管理はかなり大変になる。ヒープないのオブジェクトは任意の順序で不要になるので、現在メモリのどこが使用中で、どこが未使用なのかを処理系が管理しなければならない。このガーベージコレクションの問題に対して、「ボローチェッカー」(borrow checker)と呼ばれる参照のしくみを導入して改善したものが近年注目されているRustとなる(Rustに関しては別途述べたいと思う)。
参照型の変数は参照値だけを保持しているので、代入しても参照値がコピーされるだけとなる。よって以下のJavaのプログラムは「a[1]..10」と表示される。
int[] a = new int{1, 2, 3};
int[] b = a;
b[1] = 10;
System.out.println("a[1].." + a[1]);上記のプログラムで10を代入している先はb[1]であり、配列aに関しては何もしていないのに、勝手に10が代入されているように見えるのは、エイリアス問題と呼ばれる以下のようなaとbの示す先が同じになっているからとなる。

以上がC、Java、C#といった「静的型付け」言語となる。
動的片付け言語
Javascript、Ruby、Python等の言語は「動的型付け」言語となる。これは一言で言うと「変数に型がない」言語で、変数に型がないので、変数にはどのような型の値も格納できることになる。例えば動的型付け言語の一種であるRubyでは以下のようなコードを書くことができる。
Class Person
attr_reader :name, :age
def initialize(name,age)
@name = name
@age = age
end
end
# aに整数値を代入
a = 5
# aに文字列を代入
a = "abc"
# aにクラスのオブジェクトを代入
a = Person.new("Ruby太郎", 25)同じ変数aに、整数も文字列もクラスのオブジェクトも代入できていることが確認できる。
前述て゜、変数は「箱のようなもの」で、charやshortといった型は箱のサイズを決めていることを述べた。ここで「どんな型の値でも格納できる」ということは、すべての変数が参照型と考えることができるということになる。
参照型は、メモリ上のオブジェクトを指し示すので、サイズは一定となる。その意味ではRubyやPythonにはプリミティブ型と言う概念はない。このようにすべての型がもれなく参照型になっているとヒープがいっぱいになり、それらを回収するGCの負担が大きくなる。よって、現実の実装では、すべての型がヒープに確保されるわけではなく、整数型のように使用頻度の高い型は、変数の中に型を保持することでヒープを使わない形にしていたりするものとなる。
次回は静的型付け言語と動的型付け言語の違いについて述べる。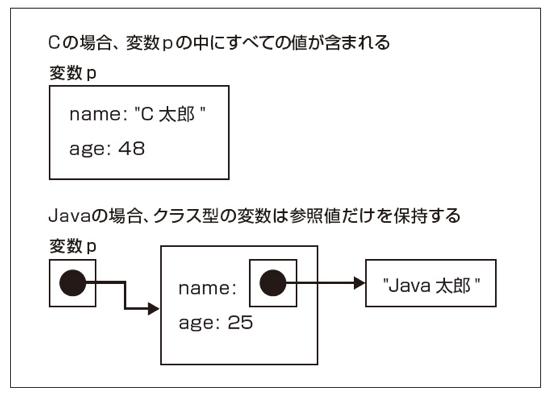

コメント