similarity(類似性)マッチング手法での戦略(5)チューニングのアプローチ

人工知能技術　ウェブ技術　知識情報処理技術　セマンティックウェブ技術   自然言語処理　機械学習技術 　オントロジー技術　オントロジーマッチング技術

前回に引き続きオントロジーマッチングより。前回はアライメントのソートのための機械学習について述べた。今回はマッチングのチューニングアプローチについて述べる。

チューニング

チューニングとは、次のような観点からマッチャーを調整して機能を向上させるプロセスとなる。

• マッチング結果の質の向上（精度，再コール，F値などで測定)。
• 実行時間、メインメモリ、CPU、帯域幅などのリソース消費量で測定される、マッ チャーのパフォーマンスの向上。

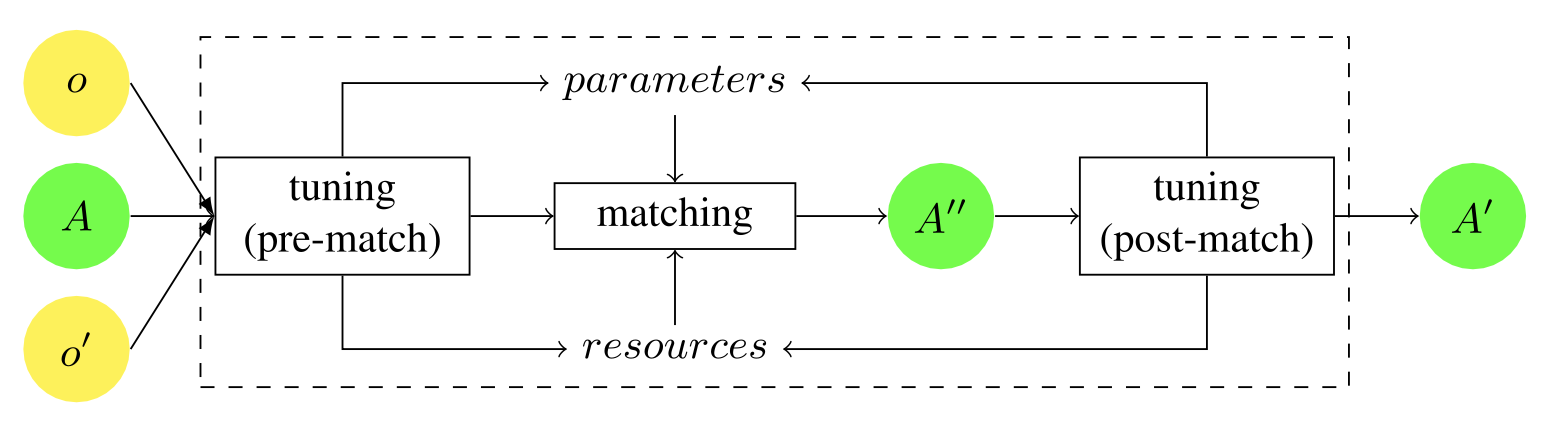
チューニングの一般的な枠組み。マッチングの前に、チューニングは、例えば入力オントロジーの特定の特性に基づいて、どのマッ チャーを採用するかを事前に決定する。マッチング後、マッチャーの出力アラインメント(A′′)は、チューナーによって評価され、マッチャーのパラメータ(およびオプションでリソース)を調整することができる。その後、マッチャーは、適応されたパラメータで新しいアラインメントを生成する。このプロセスは、チューナーがより良いパラメータを提供できなくなるまで繰り返し行われ、最後に計算されたアラインメント（A′）を返す。

調整は通常、マッチングの前に、つまりプレマッチの取り組みとして、マッチングの後に、つまりポストマッチの取り組みとして、あるいは反復的に、つまり前述の2つの段階の両方または片方を含む形で行われる。この調整プロセスは、自動、半自動、または手動で行うことができる。ユーザーは、グラフィックインターフェースを使用したり、設定ファイルを直接編集したりして、マッチングの前または後に調整を行う。例えば、マッチングの前に、入力されたオントロジーを（手動または自動で）分析し、ラベルが長いか短いか、構造がどの程度発達しているか、インスタンスがあるかどうかなど、実用的な洞察を得ることができる。この情報は、デフォルトのマッチングワークフローに対して、構造レベルのマッチャーなど、特定のマッチャーを適用するかしないかを（入力に基づいて）事前に動的に決定するために使用される。一方、マッチャーの選択は、事前に定義されたプール（通常は最大でも数十個のマッチャー）に含まれ、さらに集約されるマッチャーに適切な重み（[0 1]）を設定することで、操作上の対処を行うことが多い。これまでのところ、ほとんどのデザインタイムツールボックスでは、手動で重みを選択している（Do and Rahm 2007; Gal and Shvaiko 2009）。チューニングは、多くの場合、事前に定義されたルール（Mochol and Jentzsch 2008; Li et al. 2009; Peukert et al. )実装では、チューニングとマッチングが緊密に結びついており、チューニングは実行時のアクティビティのように見えるかもしれないが、概念的にはチューニングはマッチングの前または後に位置付けられる。

方法論的な観点から、チューニングはアーキテクチャの粒度のさまざまなレベルで適用できる。例えば、編集距離のような特定のマッチャーをマッチャーのライブラリから選択したり、選択したマッチャーのパラメータを設定したりすることができる。例えば、重み付け、1:1のアラインメントなどの制約の適用、最終的なアラインメントの選択などである。これらの例では、例えば、0.55、0.57、0.6といった特定の閾値を選択するために、十分な情報に基づいた決定を行う必要がある。ツールでマッチャーのライブラリが提供されている場合、すべての選択肢を試すには解答空間が大きすぎるため、ユーザーがマッチャーを選択し、構成し、パラメータ化するのは難しいかもしれない。そのため、これを自動的に実現するための努力がなされている。これはオントロジーメタマッチングと呼ばれることもある(Lee et al. 2007; Eckert et al. 2009)。実際には、これらの操作は常に事前に定義された数の選択肢の中で行われるため、パラメータチューニングの（洗練された）変形に還元できることが多いので、上述の操作を一緒に考えることにする。

マッチングプロセスの定義が示すように、マッチャーは、2つの入力オントロジーに加えて、入力アラインメントA、パラメータp（重みなど）、および外部リソースrを使用することができる。これらの3つの要素は、調整可能なマッチャー設定cfg = {⟨A, p, r⟩}を構成する。簡単にするために、この3つの要素を一般化して、以下のようなペアのセットで表すことができる。

\[cfg = \{⟨p_1,v_1⟩,\dots,⟨p_n,v_n⟩\}\]

上式のパラメータ(p_i)とその値(v_i)、例えば閾値は0.55となり、CFGは、可能なすべての構成の空間となる。チューニングの目的は，最適な構成，すなわち，パラメータを変更しても，マッチングの質（例：精度），マッチャーの性能（例：実行時間），またはその両方が低下しない構成を発見することとなる。たとえば，F-measureによるマッチング品質の最適化は，F-measureを向上させるcfg∗ をCFG空間の中から探すことを意味する。

使用例

eTunerは、スキーマ・マッチャーのライブラリを設計時に調整するアプローチを採用している。特定のマッチング・タスクが与えられると、適切なマッチャーと、しきい値などの使用するための最適なパラメータを選択することで、マッチング・システムを自動的に調整する。MatchPlannerは、ノードが類似性測定を表し、エッジが結果に対する条件として使用されるように、アグレガシオン関数として決定木を使用する。このような決定木は、マッチング・アルゴリズムを基本動作とする計画を表している。さらに、決定木のエッジは条件として使用されるため、これらは各マッチャーに合わせたしきい値とみなすことができる。一方、ECOMatch (Ritze and Paulheim 2011) は、ユーザが提供したアラインメントサンプルを使用し、このサンプルに関する部分的な F-measure を最適化する。ECOMatch は抹消者をブラックボックスと見なし、既成概念にとらわれない最適化技術を用いて、これらのシステムの最適なパラメータを見つける。これにより、最適なマッ チャーとパラメータの両方を選択することができる。AMSでは、ルールベースのアプローチでマッチングプロセスを適応させている。入力と出力の両方の特性は、ルールにアクセス可能な特性と見なされる。ルールは、特定のコンテキストで起動され、ワークフローを変更します。例えば、アグリゲータを追加したり（結果が複数ある場合）、基本的なマッチャーを抑制したり（品質が十分でない場合）する。

以下では、基本的なマッチャーを集約してチューニングを行うための2つの具体的な方法について、例を挙げながら詳しく説明する。これらは、積層型一般化と遺伝的アルゴリズムを用いている。

積層型一般化
積層型一般化とは、複数の学習アルゴリズムを組み合わせるアプローチとなる(Wolpert 1992)。オントロジーマッチングの観点から、このアプローチは、特定のラベルに対して、ナイーブベイズやWHIRLなどの複数の基本学習者を集約して学習することができる(Doan et al. 2003; Esposito et al. 2010)。
積層型一般化の学習フェーズは2つのステップで構成されている。最初のステップでは，各学習器の出力を集めて，新しいデータセットを作成する。まず，D⁰ = {⟨c_i , x_i ⟩}_i=1,…,m を学習データセットとし，c_i はカテゴリ，x_i は特徴量のベクトルで表されるインスタンスとする。オントロジーマッチングの観点からは，c_i はオントロジー o のエンティティであり，x_i はオントロジー o′ のエンティティとなる。ここで例えば，その属性で表される個々のc_i は x_i が割り当てられるべきカテゴリであり，オントロジーマッチングの場合は x_i に対応するエンティティとなる。過剰適合を避けるため，ここで、学習データにクエリ・インスタンスが含まれるようにするために，クロス・バリデーションを行うこととなる。具体的には，D⁰をp個の最も等しい部分，\(D_1^0, \dots, D_p^0\)にランダムに分割し，\(D_k^0\) がテスト，\(\overline{D}_k^0 = D^0 – D_k^0\) がクロスバリデーションの k 番目のクラスの学習セットとなる．レベル0の汎化器と呼ばれる基本的な学習アルゴリズム（マッチャー）がq個与えられた場合、l番目のマッチングアルゴリズムをトレーニングセット\(overline{D}_k\)に使用すると、学習されたモデル\(M_l^k\)が得られる。このようなモデルは、オブジェクトを特徴付ける特徴のベクトルが与えられると、そのオブジェクトが割り当てられるべきカテゴリである予測を返す。これがレベル0モデルとなる。x_i∈D_kに対するモデル\(M_l^k\)の予測値を\(M_l^i\)とする。クロスバリデーションの最終結果は，学習例のそれぞれに対して正確に1つの予測値からなる集合D¹となる．

\[D^1=\{<c_i,<M_1^i,\dots,M_q^i>>\}_{i=1,\dots,m}\]

第1段階の出力は第2段階の入力データとして使用され，ここではレベル-1ゼネラリストと呼ばれる他の学習アルゴリズムが採用される。そして，レベル1汎化器は，c_iに対する\(M_1^i , \dots, M_q^i\)に関するレベル1モデルM’を導出する。このように、レベル-0分類器が、エンティティの属性に関するカテゴリへの割り当ての可能性を扱うのに対し、レベル-1分類器は、分類器によって予測されたカテゴリに関する同じエンティティの同じカテゴリへの割り当ての可能性を扱う。
分類フェーズでは、新しいインスタンスxが与えられると、学習されたモデルは、ベクトル⟨M₁, …, M_q>を生成すする。これがM′の入力となり，M′はそのインスタンスの最終的な分類を出力する。
(Ting and Witten 1999)は、C4.5決定木(セクション7.5.5)やナイーブベイズ(セクション7.5.1)などの学習アルゴリズムと比較して、(1)上位モデルが下位モデルの予測ではなく信頼度を組み合わせ、(2)レベル-1汎化器として多反応線形回帰を使用した場合、分類タスクのスタック汎化で最良の結果が得られることを確認している。
マルチレスポンス線形回帰の他にも、ニューラルネットワークなど、このタスクで同様に機能するアルゴリズムがある。

積層型一般化の例。(Doan et al. 2003)より引用) 2つの基本的な学習者を使用すると仮定する。これは、(1) エンティティのラベルを扱うWHIRL学習者と、(2) エンティティのデータインスタンスを扱うナイーブベイズ学習者となる。この例では、これらのマッチャーの名前をそれぞれWHIRL、NBと略している。
トレーニングフェーズ　オントロジーoからラベルaddressを考える。
下表にオントロジーo′からの基礎学習者用の関連する学習データの例を示す。
1列目と2列目には、オントロジーo′のいくつかのエンティティのラベル（例：location）と，基礎となるデータインスタンス（例：⟨Miami,FL⟩）が記載されている。4列目と5列目は、WHIRLとナイーブベイズがクロスバリデーションによって最初の3列からの入力に基づいて生成した信頼度スコアSを記述する。
例えば，Saddress(location) = 0.5，Saddress(⟨Miami, FL⟩) = 0.8となる。最後に、WHIRL NB
最後の列は、対象となる対応関係が成立するかどうかを示す。例えば、o′からの場所は実際にoからの住所と一致するので、最後の列の対応する値は1となり、一方で、表示価格は住所と一致しないので、最後の列の対応する値は0となる。
右端の3つの列の情報は、線形回帰の入力として使用される。
ear regressionの入力として用いられる(Breiman 1996; Birkes and Dodge 2001)。WHIRLの結果とナイーブベイズ学習者の結果は、信頼度スコア（S）を表し、最後の列は、応答変数の値を表す。
列は応答変数の値を表す。最小二乗法による最小化の結果、WHIRLとラベルアドレスのペアに割り当てられた重みは0.2である。すなわちWaddress = 0.2，Waddress = 0.9となる。このWHIRL NBのの重みを解釈すると、積み重ねられた一般化トレーニングに基づいて、ナイーブベイズ学習者は広告ドレスに関する予測においてWHIRLと比較してはるかに信頼性が高いと思われる。

マッチングフェーズ  WHIRLはラベルエリアを分析し、信頼度スコアを生成する（例：⟨address,0.4⟩）。一方、ナイーブベイズ学習器は、データの内容を分析し、信頼度のスコアを生成する（例：⟨address,0.8⟩）。積層型一般化のトレーニングフェーズで得られた重みを使用することで、信頼スコアの加重平均は以下のように計算できる。0.4 × 0.2 + 0.8 × 0.9 = 0.8 となり、統合予測値 ⟨address, 0.8⟩が得られる。
似たような目的を持つ手法として、BoostingやBaggingなどがある。個々のモデル（マッチャー）の判断を組み合わせるために、ブースティングは加重多数決を、バギングは加重なしの多数決を用いる。しかし、これらは、単一の学習アルゴリズムから多様なモデルセットを得るためにデータ分布を変化させることに依存しているため、多数のモデルを必要とするが、スタッキングは少数のレベル-0モデルのみで動作することができる(Ting and Witten 1999)。SMBシステムでは、（AdaBoostアルゴリズムによる）ブースティングを利用して、プールからマッチャーを選択し、さらに組み合わせて使用することが検討されている。

遺伝的アルゴリズム
遺伝的アルゴリズムは、遺伝学と進化にヒントを得た、集団ベースの計算モデルとなる(Holland 1992)。この手法は、複雑なパラメータ最適化問題によく用いられる適応的なヒューリスティック探索手法になる。遺伝的アルゴリズムは、基本的には、解空間においてランダム化されたグローバルな探索を行う(Mitchell 1996)。
集団の個体は解とみなされ、その個体が住む環境は、これらの個体が適応される問題の目的と制約に対応している。選択プロセスでは、適者生存の原則が適用される。イテレーションと呼ばれる集団の世代を経て、個体の好ましい属性（有望な解）は進化の過程で押し進められ、弱い解は集団から駆逐されていく。遺伝的アルゴリズムの主な構成要素は以下のとおりとなる。

エンコード　元の問題空間は表現型空間として知られており、これを遺伝的空間である遺伝子型空間にエンコードして、探索を行う。その結果を出す前に、遺伝子型は表現型空間にデコードされなければならない。個体は、集団における遺伝子型のようなデータ構造として、二値、整数、実数の文字列で表現される。各文字列要素は、ソリューションの特定の特徴を表す。
ポピュレーションの初期化　最初の集団は、例えば1000個の個体を無作為に生成することで初期化されるが、問題固有のヒューリスティックを使用することも可能であり、それによって初期の個体の適合度を向上させることができる。
評価　集団内の各個体は、その品質を決定し、それぞれの繁殖機会、すなわちどの重要な情報を保存して子孫に伝えるかを決定するために、フィットネス関数を用いて評価される。これにより、フィットネス関数の値に基づいて、1000個の個体の順位が下がる。
親の選択　子孫を残すために親を選択する。例えば、ルーレットホイールサンプリングと呼ばれる、体力に比例した確率で無作為に個体を選択する方法がある。例えば、1000個の順番に並んだ個体のうち、前半の個体を親として選択することができる。
クロスオーバー　これは、2つの親の遺伝子型の特徴を組み合わせて、1つまたは2つの子孫の遺伝子型を作成するために使用される分散操作となる。確率的な操作であることが多い。
変異　親の遺伝子型を変化させて、その子孫をわずかに変化させるために用いられる、もう一つのバリエーション操作となる。これは、確率的な操作になる。この操作は、満足のいく解決策に到達しないまま早期に収束することを防ぎ、遺伝的多様性を促進するために、失われた（世代間で）情報を再び挿入する可能性があることが動機となっている。
母集団の生成　クロスオーバーとミューテーションによって新しい個体が作られ、次の世代が作られる。集団の個々の個体は、その適合性が評価される。
終了条件　適切な終了条件を決定する必要がある。例えば、フィットネスレベルが所望の精度に達した場合や、一定回数の反復処理でフィットネスが改善されなかった場合などが挙げられる。これは通常、しきい値によって処理される。

遺伝的アルゴリズムは、オントロジーマッチングの文脈において、さまざまな目的で使用されている。例えば、遺伝的アルゴリズムは、(Vázquez-Naya et al. 2010)では、複数のマッチャーの最適な組み合わせを検索して、それらの再結果を1つの値に集約するために使用され、(Wang et al. 2006)や(Elmeleegy et al. 2008)では、伸長型類似度や使用型類似度など、フィットネス関数を構成する類似度の特徴に関して、大域的に最適なアライメントを決定するために使用されている。最後に、遺伝的アルゴリズムは、アラインメント選択のための最適に近いアラインメント抽出戦略(Section.7.7)としても用いられている(Qazvinian et al. 2008)。

遺伝的アルゴリズムの例　 複数のマッチャーを最適に集約するために遺伝的アルゴリズムを使用することを考える(Vázquez-Naya et al. 2010)。課題は、グローバルなアライメント品質を最大化する重みを発見することにある。各個体は潜在的な解決策、つまり重みのセットを表しており、その合計は1になる。遺伝子型の復号化は、分離値の昇順で行われる。このプロセスは、ランダムに生成された集約、つまりそれぞれの重みのセットから始まる。例えば、5つの異なるマッチャーの結果を集約しなければならず、i番目の遺伝子型の構成は、以下の4つの分離点になる可能性がある。0.51, 0.11, 0.92, 0.57 の4つの分離点があり、その復号化（並び替え）は以下のようになる。0.11, 0.51, 0.57, 0.92. マッチャーの重みは、分離点の差として計算され、w₁ = 0.11, w₂ = 0.40, w₃ = 0.06, w₄ = 0.35, w₅ = 0.08 となる。F-measureは、フィットネス関数として使用される。親の選択はルーレットホイール法で行う。クロスオーバーは、親の体力を上回る子孫のみを次世代に渡す。変異は低確率で行われ、遺伝子型の要素をランダムに生成されたものと置き換える。ある世代の最良の個体が次の世代にコピーされる。このプロセスは、個々のフィットネス関数がしきい値よりも高くなると停止する。最も適合した個体が、最終的に選択されたソリューションとしてデコードされる。

マッチャーチューニングのまとめ
このセクションでは、チューニングのための一般的なフレームワークを紹介し、積層型一般化や遺伝的アルゴリズムなどの2つの具体的な手法について説明した。これらの手法は、基本的なマッチヤーの集約によってマッチングシステムをより良く機能させるために使用される。このテーマは近年浮上してきたものであり、さらなる調査が必要となる。実際には、照合タスクには、正しさ、完全性、実行時間、メインメモリなど、さまざまな制約や要件が適用されることが多く、多基準の判断が必要になる。主な課題は、相補性を探し、コンポーネントの弱点のバランスを取り、強みを強化することで、マッ チャーを半自動的に組み合わせることにある。例えば、集計は通常、加重平均など、事前に定義された集計関数に従って行われる。評価に関する作業は、個々のマッチャーの結果をタスクの要求と比較することで、その長所と短所を評価するために利用できる。アラインメントの質を証明できるような集計を行うための新しい方法を探さなければならない。

次回はマッチング最適化の別のアプローチであるアライメント抽出アプローチについて述べる。