Pyhtonでのガウス過程フレームワーク
前回は、Clojureを用いたガウス過程の実装について述べた。今回はPythonを用いたガウス過程のフレームワークについて述べる。これらのライブラリーはClojureからも利用することができるがそれらは別途述べる。Pythonのフレームワークとしては汎用のscikit-learnのフレームワークの中にあるものを利用するものと、専用のフレームワークGPyとがある。GPyの方が多機能であるため今回はGPyについて述べる。
GPyはShefieldの機械学習グループが提供するpythonで書かれたフレームワークとなる。これは基本的なGP回帰、マルチアウトプットGP(加重回帰)、様々なノイズモデルとスパースGPそしてノンパラメトリック回帰と潜在変数を用いたGP(GPLVM)等についてサポートしている。GPyのソースコードとインストール方法についてはgitのページに記載されている。インストールは「pip install GPy」で完了する。
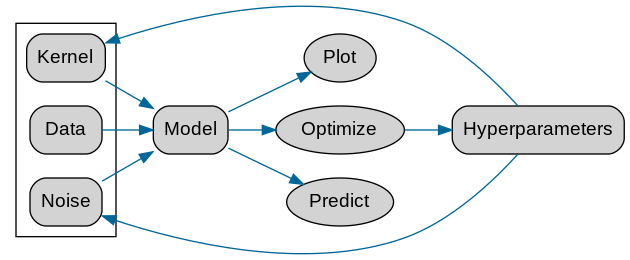
データ入力としては前回述べたClojureのものと同様にパラメータとして「Kernel」と「Noise」を入力し、それらについて予測、最適化を行うようなものとなっている。

GPyのウェブページにはtutorialとしてJupyterを用いたものが記載されている。以下にそれらのうちのいくつかを転記する。
基本的なガウス過程回帰問題
ClojureでのGPと同様に、kernelを指定して、modelを作成、optimizeして描画する。
import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.RBF(1)
# kernel = GPy.kern.RBF(1) + GPy.kern.Bias(1) + GPy.kern.Linear(1)
X = np.random.uniform(-3.,3.,(20,1))
Y = np.sin(X) + np.random.randn(20,1)*0.05
model = GPy.models.GPRegression(X, Y, kernel=kernel)
model.optimize()
model.plot()
plt.savefig('output/fig2.png')
カーネル関数を”kernel = GPy.kern.RBF(1) + GPy.kern.Bias(1) + GPy.kern.Linear(1)”とした場合の回帰結果、複雑なカーネル関数を加減で表現している。

2次元データでの回帰は以下のようになる。ここではkernelとしてMaternを用いている。
import GPy
import numpy as np
import matplotlib.pyplot as plt
kernel = GPy.kern.Matern52(2, ARD=True)
np.random.seed(seed=123)
N = 50
X = np.random.uniform(-3.,3.,(N, 2))
Y = np.sin(X[:,0:1]) * np.sin(X[:,1:2]) + np.random.randn(N,1)*0.05
model = GPy.models.GPRegression(X, Y, kernel)
model.optimize(messages=True, max_iters=1e5)
model.plot()
plt.savefig('output/fig3.png')
model.plot(fixed_inputs=[(0, -1.0)], plot_data=False)
plt.savefig('output/fig3-slice.png')
2次元の入力のうち一部を固定(インデックス0の入力を1.0)にした場合(スライス)の回帰曲線は以下となる。

スパースなガウス過程回帰
補助変数法と呼ばれるアプローチで、ガウス過程のデータ点の一部の補助変数(including input)を入力次元の代表値として扱い計算を高速化するもの
import GPy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#Sample
np.random.seed(101)
N = 50
noise_var = 0.05
X = np.linspace(0,10,50)[:,None]
k = GPy.kern.RBF(1)
Y = np.random.multivariate_normal(np.zeros(N),k.K(X)+np.eye(N)*np.sqrt(noise_var)).reshape(-1,1)
kernel = GPy.kern.RBF(1)
m_full = GPy.models.GPRegression(X, Y, kernel=kernel)
m_full.optimize()
Z = np.hstack((np.linspace(-6, -3, 3), np.linspace(3, 6, 3)))[:,None]
# Z = np.linspace(-6, 6, 12)[:, None]
m_sparse = GPy.models.SparseGPRegression(X, Y, Z=Z)
m_sparse.optimize()
m_sparse.plot()
plt.savefig('output/fig4.png')
print(m_sparse.log_likelihood(), m_full.log_likelihood()) 
Bayesian GPLVM(ガウス過程による潜在変数モデル)
ガウス過程による潜在変数モデル(Gaussian Process Latent Variable Modelとは、各特徴量xが、潜在変数zにからのガウス過程回帰により生成されると仮定し、潜在変数を計算するもので、xから直接主成分分析をものよりも、データの中に潜む特徴を抽出できる可能性を持った手法となる。
たとえば、PRMLに出てくるOIL FLOWのデータに対して、主成分分析をRで行うと以下のようになるが
library(R.matlab)
library(ggplot2)
d <- readMat('input/3Class.mat') #本文中のリンク先からダウンロード
N <- nrow(d$DataTrn)
K <- ncol(d$DataTrn)
D <- 2
## PCA
res_pca <- prcomp(d$DataTrn)
d_pca <- data.frame(X1=res_pca$x[ ,1], X2=res_pca$x[ ,2])
d_pca$class <- as.factor(apply(d$DataTrnLbls, 1, function(x) which(x == 1)))
p <- ggplot(data=d_pca, aes(x=X1, y=X2, color=class))
p <- p + geom_point(size=1.5, alpha=0.5)
ggsave(p, file='output/result-pca.png', dpi=300, w=5, h=4)
このデータに対して、Bayesian GPLVMで解析することにより、潜在的なより細かなクラスに分けることが可能となる。
from scipy.io import loadmat
import scipy.io as spio
import GPy
import matplotlib.pyplot as plt
d = spio.loadmat('input/3Class.mat')
X = d['DataTrn']
X -= X.mean(0)
L = d['DataTrnLbls'].nonzero()[1]
input_dim = 2 # How many latent dimensions to use
kernel = GPy.kern.RBF(input_dim, ARD=True) + GPy.kern.Bias(input_dim) + GPy.kern.Linear(input_dim) + GPy.kern.White(input_dim)
model = GPy.models.BayesianGPLVM(X, input_dim, kernel=kernel, num_inducing=30)
model.optimize(messages=True, max_iters=5e3)
model.plot_latent(labels=L)
plt.savefig('output/fig8.png')
計算時間は数分で終了する。ちかみに、R-Stanを使ったMCMCでのアプローチもあるが、
library(R.matlab)
library(rstan)
library(ggplot2)
d <- readMat('input/3Class.mat')
N <- nrow(d$DataTrn)
K <- ncol(d$DataTrn)
D <- 2
## Bayesian GPLVM
data <- list(N=N, K=K, D=D, Y=t(scale(d$DataTrn, scale=FALSE)))
stanmodel <- stan_model(file='model/model.stan')
fit_vb <- vb(stanmodel, data=data, init=function(){ list(x=t(res_pca$x[,1:D])) },
seed=123, eta=1, adapt_engaged=FALSE)
ms <- extract(fit_vb)
x_est <- t(apply(ms$x, c(2,3), median))
d_gplvm <- data.frame(x_est, class=d_pca$class)
p <- ggplot(data=d_gplvm, aes(x=X1, y=X2, color=class))
p <- p + geom_point(size=1.5, alpha=0.5)
ggsave(p, file='output/result-bgplvm.png', dpi=300, w=5, h=4)
こちらはMCMCでの処理となるため、高性能のマシンを利用しても数時間の処理時間がかかる。この他にもStochastic Variational Inference for GP Regression や、Parametric non-parametric Gaussian Process Regression 等も可能なフレームワークとなる。

コメント
[…] GPy – Pythonを用いたガウス過程のフレームワーク […]
[…] GPy – Pythonを用いたガウス過程のフレームワーク […]