Clojureを用いたニューラルネットと誤差逆伝播法の実装
強化学習やオンライン学習等で小規模な深層学習をアルゴリズムの中に導入することを念頭に起き、(かつニューラルネットのアルゴリズムの原理的な理解を含めて)Clojureでのニューラルネットの実装について述べる。ベースの実装はqitaでの”Clojureで0からのニューラルネット構築と隠れ層の観察“を用いて加筆を加えたものとした。
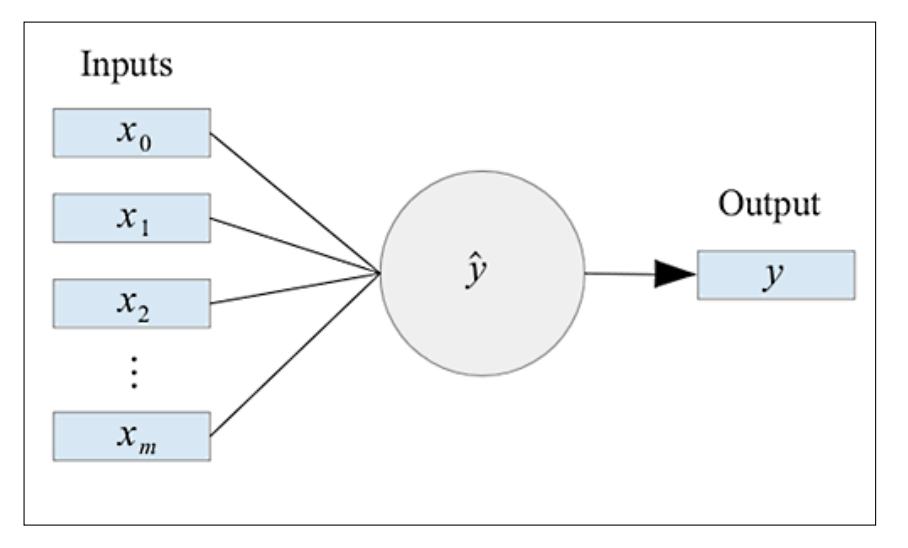
Clojureの環境設定に関しては”clojureを始めよう“等を参照のこと。またライブラリはincanterを用いたため、project.cljにincanterを加える必要がある。今回はニューラルネットワークは以下のように表される。
式としては以下のように表される。
\[\hat{y}=g\left(\sum_{i=0}^mx_iw_i\right)\ where\ g(x,w)\ is\ the\ activation\ function\]
これをClojureのコードにすると以下のようになる。
(defn unit-output [input-list w-list bias activate-fn-key]
(let [activate-fn (condp = activate-fn-key
:sigmoid sigmoid
:linear identity)]
(->> (mapv * input-list w-list) ;;(1)
(cons bias) ;;(2)
(reduce +). ;;(3)
activate-fn))) ;;(4)関数の入力としては、入力層のリスト、重みのリスト、そして活性化関数となる。出力としては(1)で重みと入力を掛け合わせた配列の作成、(2)で配列にバイアスを加えて、(3)足し合わせ、(4)活性化関数に通したものが最終的な出力となる。
活性化関数は以下のように定義する。(シグモイド関数の場合)
(defn sigmoid [x]
(/ 1 (+ 1 (exp (- x)))))出力を確認する。
(unit-output [1 2 3] [3 2 1] -2 :linear) ;;8
(unit-output [1 2 3] [3 2 1] -2 :sigmoid) ;;0.9996646498695336
(unit-output [1 2 3] [3 2 1] 1 :linear) ;;11
(unit-output [2 4 -3] [-4 2 1] 1 :linear) ;;-2
次にフィードフォワード型の多層パーセプトロンについて考える。
ここでニューラルネットを以下のように表現する。
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]{:activeta-fn …}で表されたマップデータは一つの層を示し、その中の:unit [{:bias -2 :w-list [2]}…はあるユニットの持つ重みやバイアスを示すデータとなる。
これらを使うとネットワーク上のユニットの出力は以下のように表される。
(defn network-output [w-network x-list]
(loop [w-network w-network, input-list x-list, acc [x-list]]
(if-let [layer (first w-network)]
(let [{activate-fn :activate-fn units :units} layer
output-list (map (fn [{bias :bias w-list :w-list}]
(unit-output input-list w-list bias activate-fn))
units)]
(recur (rest w-network) output-list (cons output-list acc)))
(reverse acc))))上記のコードは外側のloop関数が層の計算を、その中のmap関数が層の中のユニット一つずつに対する計算を行い、トータルでユニーラルネットの出力となる。
これらを使い、入力がスカラー量[2]、隠れ層としてシグモイド関数、スカラー出力を持つ線形関数をつなげた層計算を行うと以下のようになる。(結果は、入力データ、隠れ層、出力の3層それぞれの値が出力される)
(network-output
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]
[2])
;;([2] (0.8807970779778823 0.9990889488055994 1.670142184809518E-5) (-6.117330715367772))ニューラルネットによる学習
前述の結果を用いてニューラルネットの重みを計算する。重みは、予め用意した入力と出力のペアにより計算することができる。基本的には教師あり学習としての枠組みとなる。ニューラルネットは誤差逆伝播法と呼ばれる手法で学習が行われる。誤差逆伝播法には大きく分けて2つの過程がある。
- 予測の結果と正解の間での誤差に対し、それぞれのユニットが誤差に対してどれだけの責任があるかを求める。
- 責任の大きさの分だけ、それぞれのユニットは重みとバイアスを修正する。
この過程を出力から順番に計算していく。まず1については政界から予測の結果を引く、またこれは活性化関数を経由した出力による誤差であるため、活性化関数の微分値を考慮して、出力層でのユニットの責任の量は、誤差と活性化関数の微分にユニットの出力を与えたものを掛け合わせることで計算する。この責任量は勾配と呼ばれ以下の式で表される。
\[\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}\left(a^{(l)}\right)^T\]
ここで、a(l)は活性化値で\(a^{(l)}=g\left(\Theta^{(l)}a^{(l-1)}\right)\)と表されある層の重み行列と前の層の活性化値の積に活性化関数を適用することにより求まるものとなる。またδ(l)は活性化値a(l)と期待出力値の差分で求められる値となる。
2については、1で求めた誤差の責任の量(勾配)によって、パラメータの更新を行うものとなる。ある重みについて更新するには、責任の量以外の2つのパラメータとして、重みの対象となる下層の入力の大きさと、学習率となり、それらを掛け合わせた上で、元の重みから現在するものとなる。
\[W^{(l)}:=W^{(l)}-\left(\rho\Delta^{(l)}+\Lambda\delta^{(l)}\right)\]
以上を含めた誤差逆伝搬のClojureのコードは以下のようになる。
(defn back-propagation [w-network training-x training-y learning-rate]
(let [reversed-w-network (reverse w-network)
reversed-output-net (reverse (network-output w-network training-x))]
(loop [reversed-w-network reversed-w-network
reversed-output-net reversed-output-net
delta-list (mapv #(* (- %2 %1)
(derivative-value %2 (:activate-fn (first reversed-w-network))))
training-y (first reversed-output-net))
acc []]
(if-let [w-layer (first reversed-w-network)]
(let [output-layer (first reversed-output-net)
input-layer (first (rest reversed-output-net))
updated-w-list {:units (map (fn [{bias :bias w-list :w-list} delta]
{:w-list (map (fn [w input]
(- w (* learning-rate delta input)))
w-list input-layer)
:bias (- bias (* learning-rate delta))})
(:units w-layer) delta-list)
:activate-fn (:activate-fn w-layer)}]
(recur (rest reversed-w-network)
(rest reversed-output-net)
(map-indexed (fn [index unit-output]
(let [connected-w-list (map #(nth (:w-list %) index) (:units w-layer))]
(* (->> (mapv #(* %1 %2) delta-list connected-w-list)
(reduce +))
(derivative-value unit-output (:activate-fn (first (rest reversed-w-network)))))))
input-layer)
(cons updated-w-list acc)))
acc))))上記のコードは引数のtraining-xが入力層の出力にあたる部分、training-yが正解ラベルとなり、loopで層ごとに計算を行っている。delta-listがその層における、それぞれのユニットの責任の量を表し、
updated-w-listが、その層で更新されたそれぞれのユニットの重みとバイアスの値を表している。
connected-w-listが上層のユニットでの、中間層のこのユニットに対して接続のある部分を表している。
また、この関数の出力は、すべてのユニットの重みとバイアスが更新された新しいニューラルネットの情報を表すものとなる。
これらを用いて誤差逆伝搬を計算すると以下のようになる。
(back-propagation
[{:activate-fn :sigmoid :units [{:bias -2 :w-list [2]}
{:bias 1 :w-list [3]}
{:bias -3 :w-list [-4]}]}
{:activate-fn :linear :units [{:bias -5 :w-list [1 -2 3]}]}]
[2]
[5]
0.05)
=> ({:units ({:w-list (2.1167248411922994), :bias -1.9416375794038503}
{:w-list (2.9979761540232905), :bias 0.9989880770116454}
{:w-list (-3.9999442983612816), :bias -2.999972149180641}),
:activate-fn :sigmoid}
{:units ({:w-list (1.4896056204504848 -1.4446398871029504 3.000009283761505),
:bias -4.444133464231611}),
:activate-fn :linear})重みとバイアスの値が更新された、同じ形式の重みネットワークが出力されていることが確認できる。
ニューラルネットの初期化
学習を計算するためのニューラルネットの重みの初期化処理として、乱数を与える方法が主流となっている。以下にシンプルなニューラルネットの乱数による初期化のコードを記す。
(defn init-w-network [network-info]
(loop [network-info network-info, acc []]
(if-let [layer-info (first (rest network-info))]
(let [{n :unit-num a :activate-fn} layer-info
{bottom-leyer-n :unit-num} (first network-info)]
(recur (rest network-info)
(cons {:activate-fn a
:units (repeatedly n (fn [] {:bias (rand) :w-list (repeatedly bottom-leyer-n rand)}))} acc)))
(reverse acc))))上記のコードを使い、1=>3=>1のネットワークのフィードフォワード形式のネットを生成すると以下のようになる。
(init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num 3 :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}])
=> ({:activate-fn :sigmoid,
:units ({:bias 0.7732887809599917, :w-list (0.9425957186019741)}
{:bias 0.9502325742816429, :w-list (0.53860907921595)}
{:bias 0.6318880361706507, :w-list (0.6481147062091354)})}
{:activate-fn :linear,
:units ({:bias 0.3295752168787115, :w-list (0.9050385230268984 0.5103400587715446 0.4064520926825912)})})データセット全体に対する学習
これまでのコードを用いてトレーニングデータに対して繰り返し処理を行う。
(defn train [w-network training-list learning-rate]
(loop [w-network w-network, training-list training-list]
(if-let [training (first training-list)]
(recur (back-propagation w-network (:training-x training) (:training-y training) learning-rate) (rest training-list))
w-network)))トレーニングデータ一個ずつに対して誤差逆伝播を行う方法は確率的勾配降下法と呼ばれている。勾配法自体はニューラルネットに限定されるものではなく、最適化のために活用される手法となる。他にも、ある程度のまとまりにしてからまとめて更新する、ミニバッチと呼ばれる手法がある。それらに関する理論的詳細は”確率的最適化“に述べている。
さらに学習がうまくいっているかどうかを評価するためのデータセット全体に対する誤差を二乗誤差の和を元にして求める。
(defn sum-of-squares-error
[w-network training-list]
(loop [training-list training-list, acc 0]
(let [{training-x :training-x training-y :training-y} (first training-list)]
(if (and training-x training-y)
(let [output-layer (first (reverse (network-output w-network training-x)))
error (->> (mapv #(* 0.5 (- %1 %2) (- %1 %2)) output-layer training-y)
(reduce +))]
(recur (rest training-list) (+ error acc)))
acc))))最後に、学習を打ち切るための条件として前述の誤差の値が一定以下になった時とし、それらを入れたニューラルネットの学習を行う関数を以下に定義する。アルゴリズムの停止条件に対する理論的な考察は”機械学習における連続最適化“にて詳細を述べている。
(defn training-loop [w-network training-list learning-rate epoc]
(loop [w-network w-network, epoc epoc]
(if (> epoc 0)
(let [w-network (train w-network (shuffle training-list) learning-rate)
error (sum-of-squares-error w-network training-list)]
(println (str "epoc=> " epoc "\nw-network=> " w-network "\nerror=> " error"\n"))
(recur w-network (dec epoc)))
w-network)))例題への適用
以上を用いて具体的な例として計算する。
以下のようなsin関数を入力としてそれらをニューラルネットで近似する例を考える。
(def training-list-sin3 (map (fn[x]{:training-x [x] :training-y [(sin x)]}) (range -3 3 0.2)))
隠れ層3で入力1次元、出力1次元のニューラルネットによる推論のコードが以下のようになる。
(let [hidden-num 3
w-network (training-loop (init-w-network [{:unit-num 1 :activate-fn :linear}
{:unit-num hidden-num :activate-fn :sigmoid}
{:unit-num 1 :activate-fn :linear}]) training-list-sin3 0.05 10000)
nn-plot (-> (function-plot sin -3 3)
(add-function #(first (last (network-output w-network [%]))) -3 3))]
(loop [counter-list (range hidden-num), nn-plot nn-plot]
(if-let [counter (first counter-list)]
(let [nn-plot (-> nn-plot
(add-function #(nth (second (network-output w-network [%])) counter) -3 3)
(set-stroke-color java.awt.Color/gray :dataset (+ 2 counter)))]
(recur (rest counter-list) nn-plot))
(view nn-plot))))処理時間は数十秒で以下のような結果が出力される。
赤線が正解データ、青線がニューラルネットによる結果となる。また灰色の線は隠れ層の出力結果となる。
汎用的なニューラルネットライブラリ
これらをDSKとしてまとめ、ネットワークの構成パラメータや各種最適化手法をを入力として入れれば計算してくれる形となったものが以前述べた”pythonとKerasによるディープラーニング ディープラーニングとは何か“等で述べているKerasとなる。
Clojureでも同様なライブラリはenclog、Neuroph、FNN等いつくか存在する。
例えばenclogでは以下のコードのように非常にシンプルな形で実装でき、計算速度最適化されていて速く処理することができる。
(ns clj-ml4.som
(:use [enclog nnets training]))
(def som (network (neural-pattern :som) :input 4 :output 2))
(defn train-som [data]
(let [trainer (trainer :basic-som :network som
:training-set data
:learning-rate 0.7
:neighborhood-fn (neighborhood-F :single))]
(train trainer Double/NEGATIVE_INFINITY 10 [])))
(defn train-and-run-som []
(let [input [[-1.0, -1.0, 1.0, 1.0 ]
[1.0, 1.0, -1.0, -1.0]]
input-data (data :basic-dataset input nil) ;no ideal data
SOM (train-som input-data)
d1 (data :basic (first input))
d2 (data :basic (second input))]
(println "Pattern 1 class:" (.classify SOM d1))
(println "Pattern 2 class:" (.classify SOM d2))
SOM))
コメント
[…] これらを実装して利用するには、シンプルなモデルであれば”Clojureを用いたニューラルネットと誤差逆伝播法の実装“で述べるように数学ライブラリを利用してコードを組むこと […]
[…] ベイジアンニューラルネットワーク (BNN): “Clojureを用いたニューラルネットと誤差逆伝播法の実装“でも述べている通常のニューラルネットワークでは、重みやバイアスが固定さ […]