人工知能技術 ウェブ技術 知識情報処理技術 セマンティックウェブ技術 自然言語処理 機械学習技術 オントロジー技術 オントロジーマッチング技術
前回は言語ベースのアプローチについて述べた。今回は内部構造に基づいたアプローチについて述べる。
名前や識別子を比較する代わりに、あるいはそれに加えて、オントロジー内のエンティティの構造の情報を比較することができる。この比較は、エンティティの内部構造、つまり名前やアノテーションの他に、プロパティや、OWLオントロジーの場合はデータタイプで値を取るプロパティを比較する場合と、エンティティとそのエンティティが関連する他のエンティティとの比較に細分化される。前者を内部構造、後者を関係構造と呼びます。内部構造とは、他のエンティティを参照せずにエンティティを定義することであり、関係構造とは、エンティティが他のエンティティと持つ一連の関係のことである。予想されるように、内部構造は主にデータベーススキーマのマッチングに利用され、一方、関係構造は正式なオントロジーやセマンティックウェブネットワークのマッチングでより重要になる。今回はでは、内部構造に基づく手法についてのみ説明し、外部構造や関係性に基づく手法については、別途述べることにする。
内部構造に基づく手法は、文献では制約に基づくアプローチと呼ばれることもある(Rahm and Bernstein 2001)。これらの方法は、エンティティの内部構造に基づいており、プロパティのセット、プロパティの範囲(属性と関係)、カーディナリティまたはマルチプライオリティ、プロパティのトランジシティまたはシンメトリーなどの基準を使用して、エンティティ間の類似性を計算するものとなる。
2つのオントロジーにおいて、内部構造が類似しているエンティティや、ドメインや範囲が類似しているプロパティは数多く存在する可能性がある。そのため、これらの手法は、エンティティ間の正確な対応関係を明らかにするためではなく、対応関係のクラスターを作成するために用いられることが多い。これらの手法は通常、用語法などの他の要素レベルの手法と組み合わせて使用され、対応関係の候補数を減らす役割を果たす。明らかに互換性のないプロパティのほとんどを除去するための前処理ステップとして、他のアプローチと併用することができる。
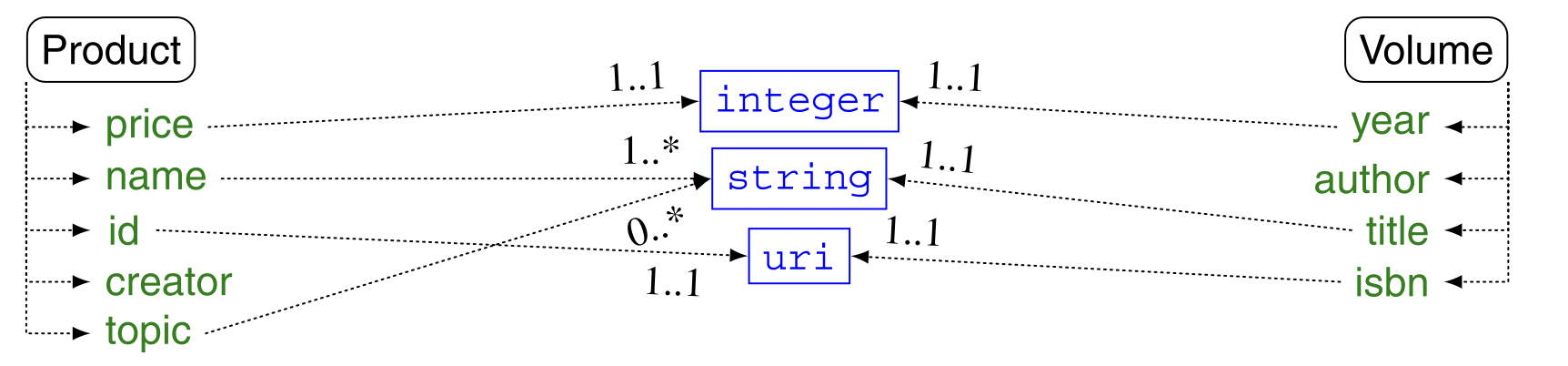
これらの方法を説明するために、下図の例でProductとVolumeのエンティティに関連するプロパティを考えてみる。

上図の要素から始めると、純粋な用語の類似性を求める手法では、全く語彙が異なっている為それらが非常に類似していると判断される可能性はない。これが、編集距離を求める手法では、yearとcreatorが同じに見える可能性があり、また、言語学的な手法で、creatorとauthorの関係を見つけやすい可能性がある。
オントロジーエンティティの内部構造を比較するということは、それらのプロパティを組み合わせて、得られた結果を合成することに還元される。システムは、次に考慮されるすべてのコンポーネント(名前、キー、データタイプ、ドメイン、カーディナリティ)または多重度の間の類似性を評価し、結果を組み合わせることができる。組み合わせ操作については別の記事で検討するが、ここでは基本的な比較に焦点を当てる。
プロパティの比較とキー
データベーススキーマでは、形式的なオントロジーとは異なり、テーブルにはキーが用意されている。これは、値によってオブジェクトを一意に識別するプロパティの組み合わせとなる。書籍の場合は、国際標準の書籍番号(isbn)、人物の場合は、名前、出生地、日付などが一般的だ。
この情報は主に、2人の個人が同じであることを認識するのに非常に役立つ。このように、キーは拡張手法において、個人を特定し、共通のインスタンスに手法を適用するための手段として使用されることがほとんどとなる。
しかしながら、キーはクラスの識別にも使用できる。同じ方法で識別された2つのクラスは、同じオブジェクトのセットを表している可能性が高い。さらに、2つのスキーマが同じクラスに異なるキーを使用していても、例えば、社会保障番号でPersonを識別する場合、社会保障番号も他のクラスのキーとみなされるなど、同じ機能を果たす二次的なキーが存在する可能性がある。そのため、キーが提供されたときに、それらのキーが高度に互換性がある(名前やタイプが似ている)場合には、クラスが同等であることがもっともらしくなる。
例えば、Product がキーとして id を持ち、Volume がキーとして isbn を持っている場合、クラスが同じであれば、これらのプロパティは対応するべきであると考えることができる。これは、両方のプロパティが同じタイプ(uri)を持っているため、可能であると考えられる。
データタイプの比較
プロパティの比較では、プロパティのデータタイプを比較する(OWLでは、関係の範囲やクラスのプロパティに適用されるRestrictionになる)。解釈を必要とするオブジェクトとは対照的に、データタイプは客観的に考えることができ、あるデータタイプが他のデータタイプにどれだけ近いかを判断することができる(理想的には、データタイプを値の集合として解釈し、これらのデータタイプを集合論的に比較することに基づいている(Valtchev 1999; Valtchev and Euzenat 1997))。
ここでは、値がコンピュータに格納される方法に対応するデータタイプ(integer、float、string、uriなど)と、特定のデータタイプのサブセットを特徴づけるドメイン([10 12]や’*book’など)を区別する。まずはデータ型について考え、ドメインについては次のセクションで説明する。
データ型は完全には分離していないが、ある型のオブジェクトを別の型のオブジェクトとして考えることができるルールや、ある型の値を別の型のメモリ表現に変換することができるルールがある(プログラミング言語ではキャストと呼ばれる)。
理想的には、データ型間の近接性は、これらが同じ型である場合には最大となり、型が互換性のある場合には低くなり(例えば、integerとfloatは一方を他方にキャストできるので互換性がある)、互換性のない場合には最小となります。また、ドメインの比較は、データ型の比較と、これらのデータ型がカバーする値のセットの比較に基づいて行われるのが理想的となる。プロパティデータタイプ間の互換性は、ルックアップテーブルを用いて評価することができる。下表にその一例を示す。

このようなテーブルは,OWLのような言語では,XML Schemaのデータ型の型階層から抽出することができる。下図の例では、uriがstringのサブクラスであることから、isbnがnameに関連している可能性が考えられる。

ProductとVolumeのデータ型の比較の例では、データ型の比較により、price と year、name と topics の両方と title、id と isbn が一致する。creator と author はオブジェクト値のプロパティであるため除外している。この照合では、期待通りの照合が行われるため、興味深い結果が得らる。しかし、間違ったもの(price-yearとtopics-title)も見つかってしまうので、これらの方法を単独で使用することはできないことが分かる。
ドメイン比較
クラスの場合はドメイン、個人の場合は値というように、対象となるエンティティによって、プロパティから得られるものは異なる。さらに、それらはセットやシーケンスで構成されている場合もある。従って、比較の際にはこの事実を考慮することが重要となる。
プロパティのタイプまたはドメインは、その解釈(値のセット)に基づいて比較することができる(Valtchev 1999)。型の比較はそれぞれの大きさに基づいて行われ、型の大きさとは、それが定義する値のセットのカード性または多重度のこととなる。2つのドメイン間の距離は、それらのサイズと共通の一般化のサイズとの差によって与えられる。この尺度は通常、特定のデータタイプに付随する最大の距離の大きさで正規化される。次の定義でこの種の尺度の例を示す。
定義 32 (Relative size distance) and e′ データタイプτ上での相対的なサイズ距離δ : 2τ × 2τ → [0 1] は, 以下のようになります.
\[\delta(e,e’)=\frac{|gen_{\tau}(e∨e’)|-|gen_{\tau}(e∧e’)|}{|\tau|}\]
genτ(…)は型表現の一般化を提供し、∨と∧は型の結合と交差に対応している。
Relative size distanceの例として、あるクラスの特性年齢を、他の3つのクラス(schoolchild, teenager, grown-up)の特性年齢と比較することを考える。最初のプロパティのドメインは[6 12]であるが、他のプロパティのドメインはそれぞれ以下のように表される。[7 14]、[14 22]および≥10で表されるとする。これらのプロパティはすべてデータ型が整数である。これらの4つのドメインを一般化したものがドメインそのものであり、それぞれの[6 12]との和集合は[6 14]、[6 22]、[6 +∞]となり、その共通部分ははそれぞれ[7 12]、φ、[10 12]となる。その結果距離は、3/|τ|、17/|τ|、|τ|-3/|τ|となる。これは、ドメイン間の距離が、ドメインが単独でカバーする値と共通でカバーする値の差に依存するという直感に対応する。
この指標には3つの利点がある。最も明らかなのは、正規化されていること。2つ目は、一般的であること(整数で表現されていない)。3つ目は、よく使われる一般的な尺度に簡単にマッピングできることとなる。
通常,一般化は型によって異なる。列挙型の場合は集合,順序型の場合は区間となる(区間の集合になることもある).密な型の場合は,領域の大きさが通常の尺度となります(実数や浮動小数点数にはユークリッド距離が使える).無限の型の場合は、(コンピュータで可能な限り大きなドメインを評価するか、実際のコーパスに関して正規化することで)適切に対処しなければならない(Valtchev 1999)。可能であれば、コーパス内の最大の距離で正規化することは、しばしば良いアイデアとなる。実際、例えば、同じ単位を使っていても、人の年齢を惑星の年齢や大きさで正規化するのは合理的ではない。このフレームワークのもう一つの利点は、共起表現として考えられ、必要に応じてドメインと比較することができる価値比較を包含していることになる。
多重性と性質の比較
プロパティは、UMLでは「多重度」と呼ばれるものによって制約を受けることがある。多重度とは、(与えられたオブジェクトに対する)プロパティの値のセットの許容できる基数になる。データ型間の互換性と同様に、基数間の互換性もテーブル・ルックアップに基づいて確立することができる。このようなテーブルの例を下表に示す(Lee et al. 2002)。

OWLでは、minCardinality、maxCardinality、cardinalityの制限により、基数や多項式を表現する。多重性は、正の整数の集合[0 +∞]のインターバルとして表現できる。そのため、整数型の領域となる。2つの多重度は、対応するインターバルの交点が空でない場合、互換性がある。多重項間の類似性の評価には,整数データ型に関する任意の尺度を用いることができるが,ここではJaccard類似度にヒントを得たより単純な距離を用いている。
値は、カーディナリティ制約が適用された特定の構造(セット、リスト、マルチセット)によって収集することができる。この場合も、(i)構築されたデータタイプと(ii)適用されたカーディナリティを比較することで、これらの構築されたデータタイプを比較することができる。例えば、2人と3人の子供の集合は、10〜12人の花の集合よりも3人の人の集合に近い(子供が人の場合)。この手法は(Euzenat and Valtchev 2004)で用いられている。
定義 34 (多重度の類似性) 2つの多重度表現[b e]と[b′ e′]が与えられたとき、 多重度の類似性は、非負の整数区間σ : 2τ × 2τ → [0 1]の間の類似性であり、 次のようになる。
\[\sigma([b,e],[b’,e’])=\begin{cases} 0&if\ b’>e\ or\ b>e’\\\frac{min(e,e’)-max(b,b’)}{max(e,e’)-min(b,b’)}&otherwise \end{cases} \]
例えば、多重度[0 6]を[2 8]、[8 12]、[0 +∞]と比較する場合、比較結果はそれぞれ0.5、0.、6/MAXINTとなる(後者は非常に低い値だが、初期の多重度と互換性があるため非NULLのままとなる)。
多重度比較の例 、ProductとVolumeの例では、多重度比較を使うと、idとisbnがともに[1 1]のカーディナリティを持ち、残念ながらpriceとyearも一致してしまうため、idとisbnをさらに一致させることができます。しかし、isは、同じ多重度([0 +∞]ではなく[1 +∞])を持っているので、タイトルにトピックではなく名前を一致させるために使用することもできる。
その他の特徴
データベースのスキーマ照合では、他の内部構造要因も考慮されている。これらの追加的な特性の中には、一意性、静的な意味的完全性制約、動的な意味的完全性制約、セキュリティ制約、al-lowableオペレーション、スケールがある(Navathe and Buneman 1986)。これらは内部特性であるため、知識モデルに大きく依存する可能性がある。
また、言語によっては、Set、List、Bagまたはmultiset、Arrayなどのコレクションコンストラクタとその互換性を考慮することも可能となる。その場合、例えば、トピックの配列や本の著者の集合など、オブジェクトの集合やリストを比較する必要がある。この場合、これらの集合の間の類似性または距離を評価するために、要素の種類に適用される類似性に応じて、一般的な技術を使用することができる。集合に関しては、これらの手法は拡張比較の文脈で前回説明されている。配列に関しては、文字列を文字の配列とみなし、パスを文字列の配列とみなした測定法を応用することができる。さらに、次項では、類似性のあるオブジェクトの集合を比較する方法に説明する。
(Ehrig and Sure 2004)では、オントロジーエンティティ間の類似性を決定するために、一連のルールを使用している。著者らは、OWLの内部構造に関連するいくつかの機能、例えば対称性や値の制限などを使用することができると指摘しているが、現時点では広く普及していないため、破棄されている。
内部構造に基づいた手法のまとめ
エンティティの名前を含む内部構造は、アルゴリズムが信頼できる基礎を提供するため、マッチングにとって非常に重要となる。また、それらを比較するための技術は効率的であり、簡単に実装できる。
しかし、内部構造は、比較対象となるエンティティーに関する情報をあまり提供しない。多くの非常に異なるタイプのオブジェクトが、同じデータタイプのプロパティを持つことがある。一方では、互換性のない対応関係を排除し、互換性のある対応関係を促進するために使用することができる。一方で、ある概念の異なるモデルが、異なる、互換性のない型を使用することは常にあり得える。これらの理由から、内部構造比較は常に他の技術と一緒に使用する必要がある。
以上内部構造比較のアプローチについて述べた。次回はデータ拡張のアプローチについて述べる。


コメント
[…] 以上言語的なアプローチについて述べた。次回は内部構造に基づく手法について述べたいと思う。 […]
[…] 前回に引き続きオントロジーマッチングより自然言語の類似性について。前回は、データの型やドメインの情報等の内部構造を領したアプローチについて述べた。今回はそれらを更に拡張したアプローチについて述べる。 […]
[…] 自然言語の類似性(similarity)(4)内部構造に基づくアプローチ […]
[…] 類似性(similarity)について(4)内部構造に基づくアプローチ […]
[…] 3.類似性(similarity)の基礎(3)言語ベースのアプローチ 4.類似性(similarity)の基礎(4)内部構造に基づくアプローチ […]