時系列データの解析の概要
時系列データとは、株価や気温、トラフィック量などの時間の経過に応じて値が変化するデータのことを呼ぶ。この時系列データに対して機械学習を適用することで、大量のデータを学習し、未知のデータに対する予測を行うことで、ビジネスの意思決定やリスク管理などに役立てることができる。
時系列データには、トレンド(傾向)、季節性、ランダム要素などが含まれる。トレンドとは長期的な傾向を表し、季節性とは周期的なパターンであり、ランダム要素とは予測できないノイズとなる。これらの要素を考慮するために、時系列データの予測では様々な手法が用いられている。
それらの中で代表的な手法としては、“RやPythonを用いた一般的な時系列解析のための実装例“でも述べているARIMA、”Prophetを用いた時系列分析について“で述べているProphet、”LSTMの概要とアルゴリズム及び実装例について“で述べているLSTM、状態空間モデルなどが用いられる。これらの手法は機械学習に基づいた予測手法で、過去の時系列データを学習して未来の予測を行うものとなる。
また、時系列データには時刻が含まれるため、過去のデータを学習し未来を予測するためには、データをトレンド成分、季節成分、残差成分に分解するなど、時系列データを適切に加工する必要があり、そこでも様々な工夫が必要となる。
今回はそれらのアプローチの中で状態空間モデルを中心に述べる。
状態空間モデルについて
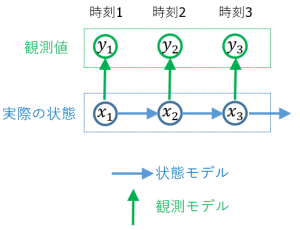
状態空間モデルは、時系列解析においてよく使用される確率モデルの一つで、観測変数と呼ばれる観測可能な変数と、状態変数と呼ばれる観測不可能な変数、さらに確率的なモデルを取り入れることで、時間的な変化や観測のノイズを取り入れ、潜在的な状態と観測されるデータの間の関係を表現するものとなる。状態空間モデルは信号処理、制御工学、経済学、統計学、機械学習などの分野で幅広く応用されている。

状態空間モデルは以下の様に数学的に表される。
- 状態方程式(State Equation): 状態方程式は、システムの潜在的な状態が時間に応じてどのように変化するかを示す差分方程式または微分方程式となる。通常、以下のように表現される。\[y(t) = f(y(t-1), u(t-1), w(t))\]
ここで、
-
- y(t)は時刻tにおける状態ベクトル(システムの内部状態)を表し
- fはシステムの状態方程式を表す関数であり、システムの特性を定義し
- u(t-1)は時刻t-1での制御入力(外部からの影響)を表し
- w(t)はプロセスノイズと呼ばれる、状態方程式内の未知の変動を表すランダムなノイズを表す。
- 観測方程式(Observation Equation): 観測方程式は、システムの状態から観測データがどのように生成されるかを表現する。一般的に次のように表現される。\[x(t) = h(y(t), v(t))\]
ここで、
-
- y(t)は時刻tにおける観測データ(通常はセンサからの観測)を表し
- hは観測方程式を表す関数であり、状態ベクトルx(t)を観測データに変換し
- v(t)は観測ノイズと呼ばれる、観測方程式内の未知のノイズを表すランダムな変動となる。
- 初期状態(Initial State): 状態空間モデルでは、初期時刻(t=0)における状態ベクトルx(0)の値が必要であり、これはシステムの初期条件を表現する。
- ノイズの性質: プロセスノイズと観測ノイズは、通常ガウス分布(正規分布)を仮定している。そのため、状態空間モデルは”不確実性と機械学習技術“で述べている確率論的なモデルとなる。またノイズがガウス分布に従う場合、カルマンフィルタなどの確率的な推定手法を用いて、フィルタリングや予測を行うことが可能となる。ノイズのハンドリングに関する詳細は”機械学習におけるノイズ除去とデータクレンジング、欠損値補間“も参照のこと。
これらを用いて、状態空間モデルでは、制御入力と観測データを元に、フィルタリング(現在の状態の推定)、予測(将来の状態の推定)、平滑化(過去の状態の推定)などの推定手法を使って、システムの状態を推定することが一般的となる。
状態空間モデルに用いられるアルゴリズムについて
状態空間モデルでは、状態推定やモデルパラメータの推定などを行うために、さまざまなアルゴリズムが使用される。以下に、主なアルゴリズムについて述べる。
- ARIMAモデル:
“RやPythonを用いた一般的な時系列解析のための実装例“でも述べているARIMAモデルは、状態変数と観測変数が線形ガウス分布に従う場合に使用されるモデルとなる。
- カルマンフィルタ(Kalman Filter):
“Clojureを用いた状態空間モデル:カルマンフィルターの実装“でも述べているカルマンフィルタは、状態空間モデルの推定に広く用いられるアルゴリズムとなる。カルマンフィルタは、観測データと状態方程式、観測方程式のモデルを組み合わせて、状態のリアルタイム推定や予測を行うものとなる。
- カルマンスムーザ(Kalman Smoother):
カルマンスムーザは、カルマンフィルタの結果を使って、過去の状態推定を修正し、より滑らかな状態推定を行うアルゴリズムとなる。カルマンフィルタがフィルタリング(リアルタイム)推定を行うのに対し、カルマンスムーザは平滑化(過去の推定値を修正)推定を行うものとなる。
- 拡張カルマンフィルタ(Extended Kalman Filter):
カルマンフィルタは線形モデルに対して適用可能だが、非線形モデルには直接適用できない。そのため、非線形モデルに対しては、拡張カルマンフィルタ(EKF)が使われる。EKFは、非線形なシステムを近似的に線形化してカルマンフィルタを適用する手法となる。
- 粒子フィルタ(Particle Filter):
“時系列データでの粒子フィルタの実装“でも述べている粒子フィルタは、非線形および非ガウス性の状態空間モデルに対して適用できるベイズフィルタリングの手法となる。この手法では、ランダムなパーティクル(粒子)を使って、状態の確率分布を近似している。特に、非線形および非ガウス性のモデルにおいて、カルマンフィルタやEKFの代替手法として広く使われるものとなる。
- ノンパラメトリックベイズ:
“ノンパラメトリックベイズとガウス過程について“で述べているノンパラメトリックベイズモデルは非線形の状態空間モデルを解くために利用されている。
- 期待値最大化アルゴリズム(Expectation-Maximization, EM):
“EMアルゴリズムと各種応用の実装例“でも述べているEMアルゴリズムは、モデルのパラメータを推定する手法で、観測データと隠れた(未知の)状態を同時に推定することができるものとなる。特に、欠損データが存在する場合や、状態ベクトルが完全には観測できない場合に有用な手法となる。欠損値補完に関しては”機械学習におけるノイズ除去とデータクレンジング、欠損値補間“も参照のこと。
状態空間モデルに利用されるライブラリとプラットフォームについて
状態空間モデルは、さまざまなプログラミング言語や数値計算ライブラリを利用して実装することができる。以下に、状態空間モデルを実装する際によく利用されるライブラリとプラットフォームについて述べる。
<Python>
- NumPy: 数値計算ライブラリであり、行列演算などを効率的に処理できる。
- SciPy: 科学技術計算用のライブラリで、線形代数、積分、最適化、信号処理などの機能を提供している。
- Statsmodels: 統計モデリングをサポートするライブラリで、状態空間モデルの推定や予測ができる。
- Kalman Filter Libraries: カルマンフィルタなどの状態推定手法を実装するためのライブラリとなる。
<R>
- dlm: Dynamic Linear Models (DLM) を実装するためのパッケージであり、状態空間モデルやカルマンフィルタの推定が可能となる。
- KFAS: Kalman Filter and Smoother パッケージは、カルマンフィルタとスムーザーによる状態推定を行うことができるものとなる。
<MATLAB>
- System Identification Toolbox: 線形および非線形システムの識別と推定を行うツールボックスで、状態空間モデルの推定に利用できる。
- Control System Toolbox: 制御システムに関する機能を提供し、制御システムの状態空間表現をサポートするものとなる。
<Julia>
- DynamicalSystems.jl: 状態空間モデルやカルマンフィルタの実装を含む、動的システムの分析に特化したパッケージとなる。
状態空間モデルの適用事例について
状態空間モデルは、様々な分野で幅広く応用されています。以下に、状態空間モデルの一般的な適用事例のいくつかを挙げてみます:
- 信号処理: 状態空間モデルは、音声信号処理や画像処理などの分野で利用されている。例えば、音声信号のノイズ除去、音声認識、画像のトラッキングなどに応用される。
- 制御工学: 制御システムの設計やモデリングにおいて、状態空間モデルがよく使用される。カルマンフィルタやカルマンスムーザなどのアルゴリズムを使って、制御システムのフィードバック制御や予測制御を実現する。
- ファイナンス: 株価の予測や金融市場のモデリングにも状態空間モデルが適用される。金融時系列データの推定や、リスク管理、ポートフォリオ最適化などに利用される。
- 経済学: 経済学においても状態空間モデルが利用され、経済指標の予測や景気の変動の分析、財政政策の評価などに応用される。
- ロボティクス: ロボティクス分野では、状態空間モデルがロボットの姿勢推定や自己位置推定、センサのキャリブレーションなどに利用される。
- バイオメディカル: 医療分野では、心拍数や血圧などの生体信号の解析や、生体システムのモデリングに状態空間モデルが用いられる。
これら以外にも、状態空間モデルは、時系列データや動的システムをモデリングする際に強力で柔軟な手法となり、特に、データにノイズが含まれる場合や未知の変動が存在する場合に有用なアプローチとなる。
最後に、主要な実装方法であるpythonとRを用いた実装例について述べる。
pythonを用いた状態空間モデルによる時系列データの解析の実装例
Pythonを用いた状態空間モデルによる時系列データの解析には、statsmodelsパッケージがよく使われる。以下は、statsmodelsパッケージを用いた状態空間モデルによる時系列データの解析の具体的な実装例となる。
まず、必要なライブラリをインポートする。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm次に、時系列データを読み込む。ここでは、AirPassengersという乗客数の時系列データを使用する。
# データの読み込み
data = pd.read_csv("AirPassengers.csv", index_col=0, parse_dates=True)データを可視化する。
# データの可視化
plt.plot(data)
plt.xlabel("Year")
plt.ylabel("Passengers")
plt.show()次に、状態空間モデルを構築する。ここでは、ARIMA(1,1,1)モデルを使用している。
# 状態空間モデルの構築
model = sm.tsa.statespace.SARIMAX(data, order=(1,1,1), seasonal_order=(0,0,0,0))状態空間モデルを推定する。
# 状態空間モデルの推定
results = model.fit()
推定結果を確認する。
# 推定結果の表示
print(results.summary())
最後に、推定結果を可視化する。
# 推定結果の可視化
results.plot_diagnostics()
plt.show()次にRを用いた解析例について述べる。
Rを用いた状態空間モデルによる時系列データの解析の実装例
Rでは、statsパッケージやKFASパッケージを用いて状態空間モデルの解析が可能となる。以下に、KFASパッケージを用いた状態空間モデルによる時系列データの解析例を示す。
例として、以下のAR(1)過程があるとする。
\[y_t=\phi y_{t-1}+\epsilon_t,\ \epsilon_t\sim N(0,\sigma^2)\]
このAR(1)過程を状態空間モデルとして定式化し、パラメータの推定を行う。
# データの読み込み
data <- read.csv("data.csv")
# KFASパッケージの読み込み
library(KFAS)
# 状態空間モデルの定義
ss_model <- SSModel(formula = ~ -1 + AR1(phi = NA),
H = NA,
Q = diag(NA, 1),
data = data)
# 初期値の設定
init_state <- c(y1 = data$y[1], phi = 0.5, sigma2 = var(data$y))
# 最尤法によるパラメータの推定
fit <- fitSSM(ss_model, inits = init_state)
# 推定されたパラメータの表示
summary(fit)
# 状態の推定値と95%信頼区間の表示
plot(states(fit), type = "l", main = "State Estimates with 95% CI")
abline(h = 0, col = "gray", lty = "dotted")
abline(h = c(-1.96, 1.96) * sqrt(fit$statesCov[, , 1]), col = "gray", lty = "dotted")
このコードでは、data.csvから時系列データを読み込んでいる。次に、SSModel関数によって状態空間モデルを定義し、fitSSM関数によって最尤法によるパラメータの推定を行っている。最後に、states関数とplot関数を用いて、状態の推定値と95%信頼区間をプロットしている。
参考情報と参考図書
時系列データ分析に関しては”時系列データ解析“に述べている。そちらも参照のこと。
General Introductions to State Space Models
-
“Time Series Analysis by State Space Methods” (2nd ed.) – James Durbin & Siem Jan Koopman (Oxford University Press, 2012)
-
A foundational text explaining state space representation, the Kalman filter, smoothing, and forecasting.
-
Includes worked examples (mostly in MATLAB, but concepts are directly transferable to R/Python).
-
-
“Dynamic Linear Models with R” – Giovanni Petris, Sonia Petrone & Patrizia Campagnoli (Springer, 2009)
-
Hands-on introduction using the
dlmpackage in R. -
Covers Bayesian state space modeling, filtering, and smoothing.
-
Applied and Computational Perspectives
-
“Applied Time Series Analysis” – Wayne A. Woodward, Henry L. Gray & Alan C. Elliott (CRC Press, 2017)
-
Covers classical and modern approaches including state space methods.
-
Provides R and some SAS code, but easily adapted to Python workflows.
-
-
“State-Space Methods for Time Series Analysis” – José Casals, Manuel J. Sotoca, Fernando Jareño & Anabel Ferrando (Springer, 2016)
-
Strong on theory with applied examples.
-
Offers computational recipes that can be implemented in R or Python.
-
Python & R Implementations
-
“Forecasting: Principles and Practice” (3rd ed., online) – Rob J Hyndman & George Athanasopoulos
-
Free online book, uses R (
forecast,fable,tsibble). -
While not exclusively about state space models, it introduces them in the context of exponential smoothing and ARIMA.
-
-
“Hands-On Time Series Analysis with R” – Rami Krispin (Packt, 2019)
-
Practical applications, including state space modeling via
forecast,bsts, andprophet.
-
-
“Applied Time Series Analysis with Python” – Aileen Nielsen (O’Reilly, 2019)
-
Focuses on practical implementation with Python’s
statsmodels,pmdarima, andpykalman. -
Includes examples of Kalman filtering and dynamic models.
-
-
“Bayesian Analysis of Time Series with Python” – Osvaldo Martin (Packt, 2021)
-
Demonstrates Bayesian state space modeling using PyMC3/PyMC4.
-
Useful for modern probabilistic programming approaches.
-
参考図書としては”

“

“

“


コメント
[…] 状態空間モデルの概要とRとPythonを用いた時系列データの解析の実装例 […]
[…] 状態空間モデルの概要とRとPythonを用いた時系列データの解析の実装例 […]
[…] ルの概要と適用事例及び実装例について”あるいは”状態空間モデルの概要とRとPythonを用いた時系列データの解析の実装例“で述べているような確率分布をベースとしたアプロ […]
[…] カルマンフィルターとカルマン平滑化: “状態空間モデルの概要とRとPythonを用いた時系列データの解析の実装例“でも述べたカルマンフィルターは、線形なダイナミクスを持つシ […]
[…] タの時間的変化を記述するモデルを開発し、データのモデリングと予測に活用する。詳細は”状態空間モデルの概要とRとPythonを用いた時系列データの解析の実装例“も参照のこと。 […]